Линии и их уравнения

Итак, при наличии системы координат каждой точке плоскости соответствует пара действительных чисел и, наоборот, каждой паре чисел соответствует определенная точка плоскости. Можно установить, что линиям на плоскости соответствует некоторое уравнение с двумя переменными x и y в декартовой системе координат и переменными r и  в полярной. Связь между уравнениями и линиями позволяет свести изучение геометрических свойств линий к исследованию аналитических свойств соответствующих им уравнений. Линии на плоскости соответствует некоторое уравнение с двумя переменными, которому удовлетворяют координаты любой точки, лежащей на линии, и не удовлетворяют координаты ни одной точки, не лежащей на ней. Такое уравнение называют уравнением данной линии. Входящие в него координаты x и y (или r и ) произвольной точки линии называются текущими координатами.

Уравнение линии на плоскости может быть аналитически задано в явном виде - y=f(x), =f() или неявном виде - F(x,y)=0, F(,)=0. Полярную систему координат удобно использовать, когда длина радиуса-вектора точек, лежащих на линии, связана аналитической зависимостью со значением угла поворота .

Примеры уравнений линий в декартовой и полярной системе координат

1.Уравнение прямой, отсекающей на оси Y отрезок величины b: y=kx+b, где k - значение tg угла наклона прямой к оси ОХ; параметр k называется угловым коэффициентом прямой. Уравнение линии задано в явном виде (рис. 8).

2.Уравнение линии, являющейся геометрическим местом точек, для которых расстояние до некоторой точки О с координатами а и b есть величина постоянная (обозначим ее через R). Выпишем условие равенства константе R расстояния от любой точки М(x,y) до точки O(a,b): . Возведя обе части равенства в квадрат, получаем каноническое уравнение окружности:

(x-a)²+(y-b)²=R²

Если система координат выбрана так, что центр окружности совпадает с началом координат, то a=0, b=0 и уравнение окружности принимает вид:

x²+y²=R²

Уравнение линии в этих примерах задано в неявном виде.

3.Уравнение окружности в полярной системе координат.

Введем полярную систему координат, центр которой совпадает с центром окружности, а направление полярной оси, например, горизонтальное. Окружность определяется, как геометрическое место точек, для которых расстояние до некоторой точки О есть величина постоянная (эту величину мы обозначали через R). Следовательно, уравнение окружности в полярных координатах: r=R

Окружность дает простейший пример линии, уравнение которой от перехода к полярной системе координат упрощается.

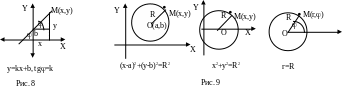
На рисунке 9 приведена окружность и ее уравнение в разных системах координат. Одновременно мы показали на этом простом примере, что вид линии не зависит от того, в какой системе координат написано ее уравнение. От выбора системы координат зависит лишь вид уравнения.

Рассмотрим примеры еще 2 кривых, длина радиуса-вектора которых связана аналитической зависимостью со значением его угла поворота . Уравнения этих кривых удобно задавать именно в полярной системе координат.