Тригонометрические функции

Тригонометрические функции угла  определяются с помощью тригонометрического круга радиуса r=1, а также из прямоугольного треугольника (для острых углов) (рис. 1).

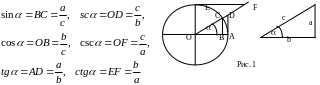
Углы измеряются в градусах (0360) (каждый градус состоит из 60' (минут), каждая минута из 60''(секунд)), или в радианах (02). Полный угол состоит из 1296000''. При измерении угла в градусах, минутах, секундах возможное значение величины угла – рациональное число m/n, где n=1296000, а m – номер ближайшей секунды. Измерение углов в радианах - это фактически отождествление угла с дугой окружности единичного радиуса, на которую он опирается, т.е. величина угла может принимать любое значение, а не одно из 1296000 возможных. Угол в один радиан - это угол, который стягивается дугой, длина которой равна радиусу окружности. Длина окружности пропорциональна ее диаметру. Обозначение для этого коэффициента пропорциональности - . Длина окружности единичного радиуса равна 2. Тем самым, величина полного угла в радианах тоже равна 2. Переход на радианы позволяет указывать величину угла с помощью линейной меры. Если прокатить колесо единичного радиуса по земле на один оборот, то след от колеса будет иметь длину 2. Этот отрезок и будет соответствовать полному углу 2 радиан. Таким образом, можно сказать, что в градусах, минутах, секундах можно задавать "рациональные" значения углов, а в радианах - любые. Для практических целей обычно вполне хватает указания величины угла в градусах, минутах, секундах, это и удобнее, а в аналитических формулах в качестве аргумента используется значение угла, заданное в радианах.

В качестве иллюстрации приведем построение графика синуса (рис. 2а). График строится на отрезке, длина которого равна длине окружности единичного радиуса, т.е. 2π. Для того, чтобы построить 12 опорных точек графика, окружность и горизонтальный отрезок длины 2π делим на 12 равных частей. Значение синуса угла равно длине полухорды. Откладываем по вертикали длины соответствующих полухорд.

На рисунке 3 показано, как из свойств равностороннего треугольника (рис 3а) и равнобедренного прямоугольного треугольника (рис. 3б) с помощью теоремы Пифагора получить значения тригонометрических функций для углов 0º, 30º, 45º, 60º, 90º.

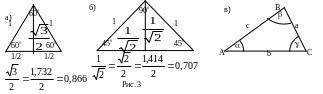
Таблица значений тригонометрических

функций для углов 0º, 30º,45º,60º90º

градусы х радианы х	0 0	30 /6	45 /4	60 /3	90 /4
sin x	0				1
cos x	1				0
tg x	0		1		
ctg x			1		0

Пересчет градусной меры в радианную производится с помощью пропорции . Длина дуги l окружности радиуса r, опирающейся на центральный угол , равна (рис. 2б).

Формула показывает, что длина дуги пропорциональна радиусу. В силу этого можно сказать, что угол в один радиан стягивается дугой, длина которой равна радиусу окружности. Величина центрального угла не зависит от радиуса.

=3,1415926, 1радиан=5717,5', arc1=2π/360=0,01745, 1/=0,31831