Некоторые стандарты планировки интерьера храма

Если размер подкупольного "квадрата" измерить в футах (греческих – 308-309мм или римских 295-296мм), то, как правило, используются размеры: 25, 20, 16, 15, 12, 10 футов. В летописи упоминается размерение с помощью "пояса Шимона", но эта мера, скорее всего, равна 4 футам. При описании геометрии храма сторона подкупольного "квадрата" может использоваться в качестве "модуля" - исходной меры, которая является начальным звеном в цепи соразмерности всех элементов сооружения.

Слово "квадрат" мы снабдили кавычками, так как вместо точного квадрата часто использовался "живой" квадрат - близкий к квадрату прямоугольник, вытянутый чаще всего вдоль продольной оси храма.

В описании встречаются следующие пропорциональные отношения сторон подкупольного квадрата.

рациональные соотношения:

1:1 - точный квадрат;

20:210,95 (21:201,05) или 21:221.05 (22:210.95)

20:21 - "квадрат" вытянут в продольном направлении (рис.4а), 21:20 - в поперечном;

10:11≈0,9 (11:10≈1,1);

5:60,83 (6:5=1,2);

4:5=0,8 (5:4=1,25);

а)

иррациональные соотношения (построение с помощью циркуля и линейки):

1,155:1 (0,866:1) (рис. 4б,в) - соотношение между стороной и высотой равностороннего треугольника, ( );

- соотношение между стороной и диагональю квадрата, на рисунке 4г дано построение, начиная с нижней стороны, на рисунке 4д построение прямоугольника такого же размера, но выполненное от центра;

0,894:1 (1,118:1) - соотношение между стороной квадрата и диагональю полуквадрата - ( ).

"Живой квадрат" с соотношением сторон =1,118:1 можно построить двумя способами - с помощью диагонали полуквадрата (рис 5а) и как катет прямоугольного треугольника, короткий катет которого равен 1, а гипотенуза - 1.5 (рис.5в), так как согласно теореме Пифагора длина второго катета вычисляется по формуле: .

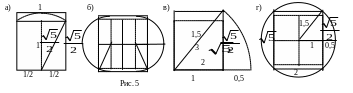
На рисунках 5а и 5в дано построение, начиная с нижней стороны, на рисунках 5б и 5г те же построения выполняются от центра.

Толщина столбов выражается в долях стороны подкупольного квадрата. Самые распространенные значения: 1/5=0,2 и 1/4=0,25. Получить 1/5 можно геометрически, не прибегая к измерениям, описав окружность вокруг квадрата со стороной 1 (рис. 6а). Для получения 1/4 также не требуется измерения - достаточно веревку, длина которой равна стороне квадрата, сложить два раза. Сводная таблица, приведенная в книге Афанасьева, демонстрирует, что эти 2 алгоритма соблюдаются только для больших подкупольных квадратов. При уменьшении размеров храма толщина столбов и стен не уменьшалась пропорционально размерам храма, толщина меньше метра практически не встречается и, вместо долей 0,2 и 0,25 от величины стороны подкупольного квадрата, у малых храмов появляются доли 0,3-0,4. Например, сторона подкупольного "квадрата" храма Покрова на Нерли 10 футов - 3м10см. 310:478см. И размер столбов определяется диагональю полуквадрата (рис. 6б). При таком построении толщина столбов будет составлять примерно 0,3 часть от стороны квадрата и получается равной 96-98см. Точнее, если принять сторону квадрата за единицу, то толщина столба при таком построении равна /20,309. Эти же дуги служат и для "растягивания" квадрата вдоль продольной оси, когда центром растяжения является центр квадрата. Очень редки круглые столбы, встречаются столбы восьмиугольной формы. Неизвестно, каким именно способом чертил восьмиугольник создатель таких столбов, никаких письменных источников того времени, освещающих эту проблему нет. На рис. 6в приведен очень простой и верный, несмотря на отсутствие доказательства, способ построения восьмиугольника, содержащийся в немецком руководстве по практической геометрии, написанном во второй половине ХV века. Этот учебник наверняка вобрал в себя многовековой опыт строителей.

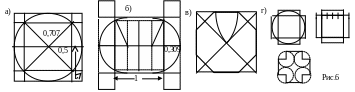
0,707-0,5=0,2071/5

Столбы имеют крестчатую форму. Размер лопаток чаще всего определяется каким-нибудь простым построением, например, тем же построением, что и размер столба - проведением окружности вокруг сердцевины столба, или равен просто 1/4 или 1/2 толщины столба (рис.6г). Но точность их сооружения, как правило, очень невелика. Естественно, встречаются столбы и не очень правильной формы (о них мы говорить не будем, обсуждение их формы оставим архитекторам).

Ширина нефов также является рациональной (выражается в целых долях) или иррациональной (строится с помощью циркуля) функцией стороны подкупольного квадрата. В размерении нефов, как продольных, так и поперечных, могут участвовать и обе стороны подкупольного "квадрата", и его диагональ или диагональ половины подкупольного "квадрата".

Ширина боковых нефов Киевской Софии, прилегающих к центральному нефу, определяется тем же построением, что и у Константинопольской Софии - диагональю половины подкупольного квадрата (рис 7а). Такое построение задает разбивку поперечной оси храма в отношении: :1:. Этот же алгоритм построения может выполняться и тогда, когда подкупольный квадрат слегка вытянут.

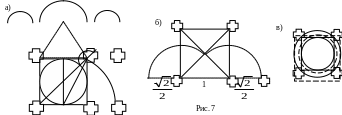
Ширина боковых нефов Новгородской Софии, прилегающих к центральному нефу, определяется полудиагональю подкупольного квадрата (рис. 7б) (отношение 0.707:1:0.7077:10:7). В некоторых планах в построениях участвуют равносторонние треугольники (построение таких треугольников с помощью циркуля осуществить очень легко) - и для определения центра апсиды, и для определения ширины нефа или всего храма.

Самые простые рациональные соотношения - ширина боковых нефов равна 1/2 или 3/5 стороны подкупольного квадрата. В качестве ширины поперечных нефов используются те же самые рациональные и иррациональные функции сторон подкупольного "квадрата". На выбор ширины нефов влияет много обстоятельств. Это и практические соображения, и стремление соблюсти общие пропорции здания, и связь их величины с внешним обликом здания.

Мы видим, что древними мастерами широко используются отрезки, длины которых суть иррациональные величины и даже (гипотенуза прямоугольного треугольника, один катет которого равен 1, а второй ). Они несоизмеримы с единицей, то есть их нельзя измерить совершенно точно, как это принято в наши дни, с помощью измерительной линейки, состоящей из метров, сантиметров и миллиметров (или саженей, локтей и пальцев или футов и дюймов), но их легко построить с помощью циркуля и линейки. Древними мастерами использовались рациональные приближения для их значений, обеспечивающие удовлетворительную с точки зрения практики точность.

Внутренний диаметр барабана определяется стороной подкупольного квадрата, а внешний диаметр барабана этой стороной и толщиной столбов (рис. 7в). В простом случае проекция барабана - это вписанная и описанная окружности подкупольного квадрата. Желая облегчить вес купола, стены барабана старались сделать как можно более тонкими. Увеличение внутреннего диаметра увеличивает внутренне пространство купола, но лишает внутреннюю стену барабана опоры на подпружные арки. Поэтому проще добиться уменьшения веса барабана за счет внешних размеров. Так что иногда стенки барабана делали, чуть ли не вдвое тоньше опорных столбов.

Мы не касаемся вопроса о том, как проектировалась алтарная часть храма - как выбирались ширина восточного нефа, центр и радиус апсид. Это вопросы скорее архитектурные, чем геометрические. Так как мы обсуждаем построения, которые использовались в работе древними мастерами, отметим примеры использования трехцентровых дуг.

Несколько необычная форма апсиды в одном из храмов - это не дуга окружности, а трехцентровая дуга, имеющая форму подковы (рис. 8а). Сначала вычерчивается полуокружность, затем радиусом, равным диаметру, из конечных точек диаметра проводятся дополнительные дуги. Форму трехцентровой дуги имеет подпружная арка Успенского собора в Чернигове (рис. 8б). Пролет арки делится на 8 частей, средняя часть описывается радиусом, равным 5 частям, боковые части радиусом, равным 3 частям (еще одно использование тройки 3, 4, 5).

В нутренняя планировка русского храма целиком определяет наружный вид здания, так как наружные фасады членятся пилястрами, расположенными на тех же уровнях, что и внутренние столбы, закомары повторяют очертания сводов, а высоту здания и его частей, как правило, можно найти на его горизонтальном плане.

Уровень точности, с которой воплощался геометрический замысел архитектора, был в те времена не слишком высок. Планы, воспроизведенные в масштабе 1:100 или 1:50, демонстрируют иной раз видную невооруженным глазом перекошенность, как подкупольного квадрата, так и всего плана, разницу в ширине симметричных нефов, столбы неправильной формы и т.д. А уж разница в 10 см и вовсе не видна на плане, выполненном в таком маленьком масштабе. Несмотря на простоту алгоритмов, добиться хорошей точности при больших длинах не удавалось. Кроме того, в "правильный" геометрический чертеж архитекторы, знакомые с тайнами восприятия человеком объемных предметов, вносят поправки, служащие для того, например, чтобы вызвать иллюзию большей глубины интерьера или большей высоты купола, или сознательно вносят небольшие неточности, что, как показывает опыт, улучшает общее впечатление.

Приведем некоторые схемы, которые представляются первым приближением построения планов древнерусских храмов в домонгольский период, "математика" которых может быть связана с "золотыми" пропорциями. Напоминаем, что речь будет идти о математической модели, дающей лишь первое приближение, а не о точном описании конкретных храмов.

Изучение планов, собранных в монографии К.Н.Афанасьева, показывает, что для планов храмов, имеющих развитую западную часть характерно соотношение длины и ширины интерьера близкое к золотому. Кроме 4-х столбов подкупольного пространства в таких храмах имеются дополнительные опоры в виде 2-х или даже 4-х столбов, а иногда целая внутренняя стена, отделяющая нартекс. Опишем простейшие математические модели таких планов, построенные на основе представленных в монографии материалов. Сначала рассмотрим схемы, которые можно построить безо всякого циркуля на клетчатой бумаге. При построении плана, имеющего пропорции "золотого" прямоугольника, мы будем пользоваться целыми числами и простейшими дробями, т.е. не выйдем за пределы расчетов, доступных древним мастерам. В масштабе 1:50 эти схемы являются неплохим приближением для плана нескольких храмов.

Схема плана, основанная на делении поперечной оси в пропорции: 1:2:1:4:1:2:1

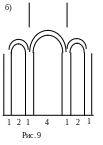
На рисунке 9а изображен план, в котором поперечный разрез храма конструируется с помощью пропорциональных соотношений 1:2:1:4:1:2:1, то есть величина стороны подкупольного квадрата - 4 единицы, толщина стен и столбов равна 1, ширина боковых нефов равна 2.

а)

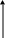
5

6

10

5

2

1

4

1

2

6,25

10

Самый простой вариант описания этой схемы плана - внутреннее пространство храма, включая апсиды - прямоугольник, который можно разбить на квадрат со стороной 10, к которому с восточной стороны пристроены апсиды (вписаны в прямоугольник 310), а с западной – нартекс (также прямоугольник 310), отделенный от молитвенной части стеной или столбами.

Второй вариант описания того же плана - квадрат со стороной 10, в который входит подкупольное пространство и апсиды, и примыкающий к нему с запада прямоугольник со сторонами 10 и 6. Это описание напоминает построение "золотого" прямоугольника с помощью диагонали полуквадрата. Западная сторона этого квадрата задает положение западной стороны подкупольного квадрата. Прямоугольники с отношением сторон 16:10=8:5=1,6:1 и 10:6=5:31,67 близки к золотым. Пропорции 8:5 и 5:3 встречается у древних мастеров очень часто. Центр подкупольного квадрата совпадает с центром плана. Если в качестве короткой стороны маленького прямоугольника взять 6+1/4=0,625, то получим пропорции совсем мало отличимые от "золотых": 16,25:10=1,6251,618 и 6,25:10=0,6250,618 (точность соблюдения пропорций: 0,007:1,61000,5%). Отношение ширины бокового нефа к стороне подкупольного квадрата: 2:4=0,5. На рисунке 9б приведена грубая схема внешнего вида западного фасада такого храма.

Схема плана, поперечный разрез которого описывается с помощью чисел 1, 3, 5, 8, 13, 21

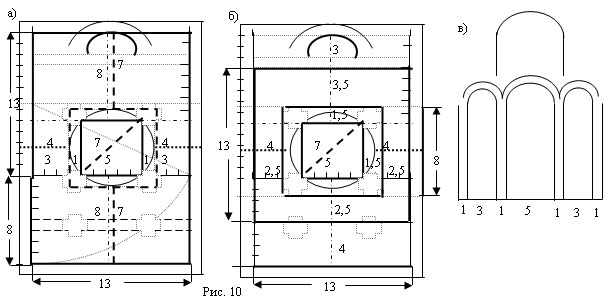
Поперечный разрез храма конструируется с помощью пропорциональных соотношений 1:3:1:5:1:3:1. Величина стороны подкупольного квадрата - 5 единиц, толщина стен и столбов равна 1, ширина боковых нефов равна 3. Схему плана можно нарисовать на клетчатой бумаге так, как это представлено на рисунках 10а,б. Схема западного фасада, имеющего такие пропорции, представлена на рисунке 10в.

Похожий вид имеет план самого древнего сохранившегося до наших дней храма - Спасо-Преображенского собора в Чернигове (заложен в 1036г.). Похожую разметку имеют многие планы "золотой" или близкой к "золотой" пропорции.

Не только пропорции поперечного разреза, но и основные пропорции продольного разреза также у многих храмов имеют общие черты. На схеме видно, что в плане внутреннее пространство храма, включая апсиды - прямоугольник с отношением сторон 21:13. Его можно разбить на квадрат со сторонами 13:13, расположенный в восточной части храма, и прямоугольник со сторонами 13:8 в западной части. Западная сторона подкупольного квадрата, сторона которого в тех же единицах измерения равна 5, лежит на западной стороне квадрата 13:13. Отношение ширины бокового нефа к стороне подкупольного квадрата 3:5=0,6.

Мы видим, что пропорции прямоугольников, из которых строится план, описываются с помощью последовательности целых чисел: 1, 3, 5, 8, 13, 21. Эта последовательность выделялась (из натурального ряда) архитекторами еще в античные времена. Если вставить на второе место число 2, то получим начало последовательности Фибоначчи, о свойствах которой мы уже рассказывали.

Отношение соседних членов последовательности Фибоначчи очень близко к "золотому":

(1+):1=Ф:1=1:21:131,615:11,618:1 (точность 0,003:1,61000,2%),

(1+):1=Ф:113:8=1,625:11,618:1 (точность 0,007:1,61000,5%),

3:5=0,60,618 (точность 0,018:0,61002%).

Таким образом, данное нами описание пропорций плана храма с помощью последовательности целых чисел 1, 3, 5, 8, 13, 21 дает неплохое с практической точки зрения рациональное приближение "золотых" пропорций.

Центр подкупольного квадрата по этой схеме находится в центре прямоугольника плана. На рисунке 10б изображено построение того же плана от центра (считается, что разбивка плана в соответствии с традициями, пришедшими из Греции, производилась мастерами именно от центра). Если принять, что ширина лопатки столба равна половине толщины столба, то в основе построения окажутся 3 концентрических квадрата со сторонами 5, 8 и 13. Апсиды с восточной стороны, нартекс с западной со своими столбами примыкают к квадрату 1313.

Заметим, что точность, с которой работали древние мастера, была порядка 1-2%. Например, для подкупольного квадрата со стороной 25 футов (≈7,7м) длина диагонали составляет примерно 11м, а разница в длинах 2-х диагоналей составляет 20см. Длины диагоналей подкупольного квадрата различаются примерно на 2%. Разница в ширине боковых нефов составляет 3см при том, что их размер равен примерно 150см (2%) и т.д.

Чтобы получить пропорции северного и южного фасадов, примем для радиуса апсиды грубую оценку. Как правило, диаметр апсиды на величину 2-х лопаток меньше восточной стороны подкупольного квадрата. Так что будем считать, что радиус апсиды равен 2 единицам. Заканчивается апсида столбами с лопатками, заменяющими восточную стену и это дает нам длину храма снаружи без апсид, равную 20 единицам (21-2+1). Тем самым членение северной и южной стороны храма с востока на запад для схемы, приведенной на рисунках 10а,б, можно описать пропорцией: 1:2:1:4:1:5:1:3:1:3:1.

В наших схемах для барабана примем самый простой вариант, когда внешний диаметр барабана равен малой стороне подкупольного квадрата в сумме с двумя столбами. Тогда для схемы 1 2 1 4 1 2 1 членение плечо - барабан - плечо описывается пропорцией 3:6:3=1:2:1, так как длина плеча от внешней стенки барабана до края стены храма равна толщине стены плюс ширина бокового нефа, т.е.1+2=3, а диаметр барабана это две толщины столба плюс сторона подкупольного квадрата, т.е. 1+4+1=6. Для схемы 1 3 1 5 1 3 1 получается пропорция 4:7:4. Эти схемы демонстрируют, как отражается выбор схемы на внешнем облике здания.