Производные «золота»

Самое простое разбиение отрезка на две части - это деление отрезка точно пополам. Некоторое смещение от центра отрезка точки деления отрезка на две части улучшает зрительное впечатление. Эта цель достигается с помощью деления в "золотой" пропорции. Обмеры показали, что для того, чтобы смягчить слишком резкое отклонение золотого сечения от точного деления пополам, мастера применяли золотое сечение повторно, что приводило к делению отрезка в пропорции , которую с точностью до 3-х знаков можно описать рациональным соотношением 528:4721,118. Это отношение называют производной золотого сечения (рис.13).

Если еще раз выполнить золотое сечение отрезка, получится деление отрезка в пропорции 507:4931,028. Следующее сечение, дающее деление отрезка в пропорции 501:4991,004, практически неотличимо от точного деления отрезка пополам (все эти значения выражаются через рациональные функции, зависящие от ).

Если архитектор выбирает для себя некоторый способ гармонизации, то ему нужен циркуль, настроенный на выбранную пропорцию.

Циркуль без изменения раствора позволяет построить 3 отрезка (рис: 14). Три отрезка, построенных циркулем, настроенным на "золотую" пропорцию, обеспечивают одинаковое пропорциональное деление целого и части.

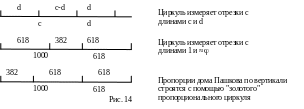
Очень интересными свойствами обладает прямоугольный треугольник, у которого "золотым" является отношение гипотенузы к меньшему катету (рис. 15а). Если а - длина меньшего катета, то согласно теореме Пифагора и соотношению Ф²=1+Ф, его второй катет равен . То есть длины его сторон образуют геометрическую прогрессию 1, q, q² с множителем q= . Для примера на рисунках 15б,в продемонстрированы фигуры, которые можно построить с помощью треугольников такого вида ( -треугольник) - -ромб и логарифмическую спираль.

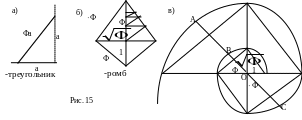
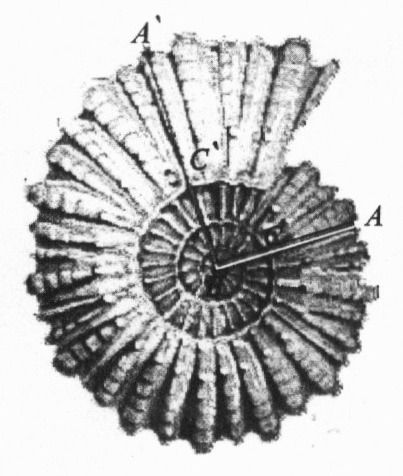
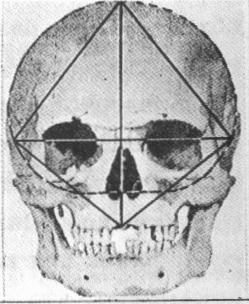
Пропорции -ромба (рис. 15б) встречаются в природе - этот ромб просматривается в форме черепа, в форме морских раковин [Шевелев].

Спираль из дуг, построенная вокруг улитки -треугольников суть логарифмическая спираль. Увеличению угла на /2 соответствует увеличение радиуса-вектора этой спирали в раз (рис. 15в). Для выполнения этого чертежа можно воспользоваться тем, что больший катет треугольника становится меньшим катетом следующего треугольника, а гипотенуза предыдущего треугольника – большим катетом следующего. С поворотом на угол  длина радиуса-вектора возрастает в Ф раз. Центр спирали О делит любой диаметр (АС, ВС) в "золотой" пропорции, и точка В делит ОА в "золотом" отношении (в главе 7 мы напишем уравнение этой спирали и докажем это). Такую форму имеет морская раковина Nautilus - живое доказательство того, что золотое сечение определяет природные ритмы развития.

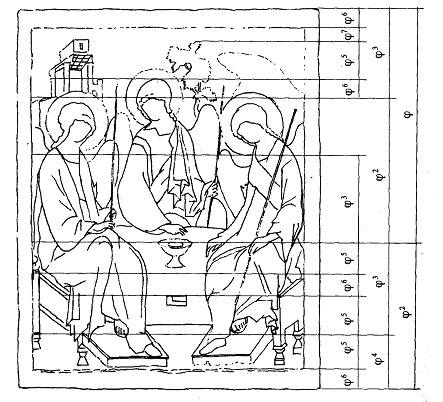
« Троица» Рублева и золотые пропорции

Ниже, мы еще раз встретимся с треугольником - он лежит в основе пропорций пирамиды Хеопса.

Задачи для самостоятельного решения.

1. Построить с помощью циркуля и линейки нормальный полиграфический прямоугольник.

2. Построить с помощью циркуля и линейки рядом с одним квадратом другой квадрат, площадь которого вдвое меньше.

3. Для измерения высоты дерева в землю воткнули шест длиной 2м и измерили длину тени от шеста (3м) и от дерева (15м). Какова высота дерева?

4. Разрез Пантеона в Риме (II в.н.э.) приведен на чертеже в масштабе 20мм – 20м. Диаметр круга на чертеже равен 4,3см (рис. 16). Найти высоту стен и купола.

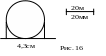
5. Выписать 12 первых членов последовательности чисел Фибоначчи.

6. Построить с помощью циркуля и линейки

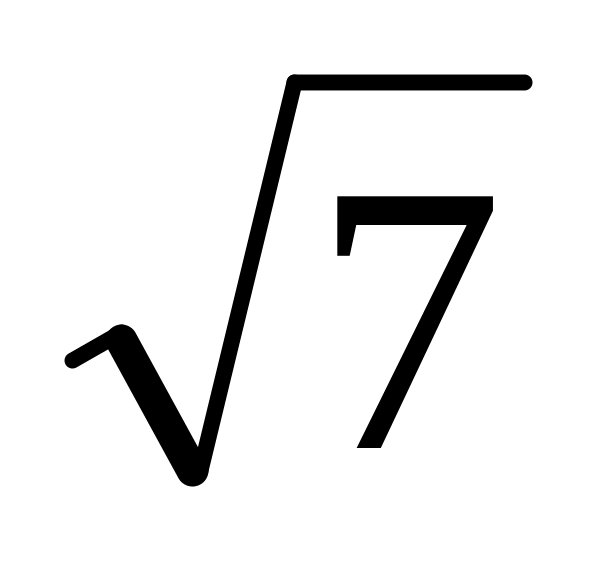
7. Построить "золотой" прямоугольник по большой стороне.

8. Построить "золотой" прямоугольник по малой стороне.

9. Построить спираль Дюрера

10. Построить "золотой" прямоугольный треугольник.

11. Построить "золотой" равнобедренный треугольник (углы которого равны 72, 72 и 36.

12. Построить последовательность отрезков, длины которых находятся в пропорциональном отношении 1:Ф:Ф²:Ф³…

13. Вычислить первые 5 членов геометрической прогрессии: 1, , Ф, Ф, Ф²,….

14. Построить последовательность отрезков, длины которых находятся в пропорциональном отношении 1: :Ф: Ф:Ф²,….

15. Построить правильный пятиугольник по заданной стороне.

16. Построить 5 концентрических окружностей, расстояния между которыми суть геометрическая прогрессия с множителем Ф. Поделить окружности на 16 равных частей. Получившуюся сетку использовать для построения рисунка из спиралей.

17. По репродукции пейзажа с линией горизонта определите, делит ли линия горизонта картину по высоте в «золотом» отношении.

18. Для прогрессии r², r⁴, r⁶,…, для которой выполняется 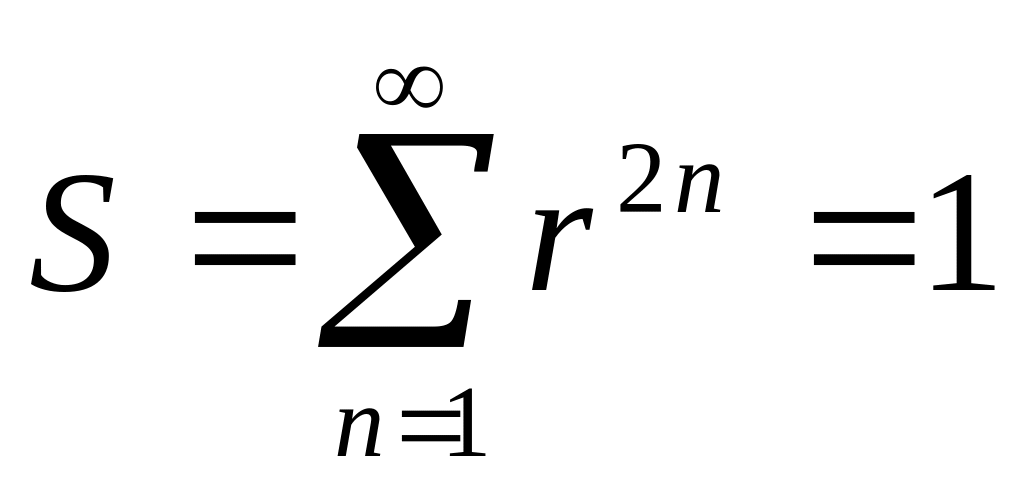, найти значение r.

19. Для прогрессии r, r³, r⁵, r⁷,…, для которой выполняется 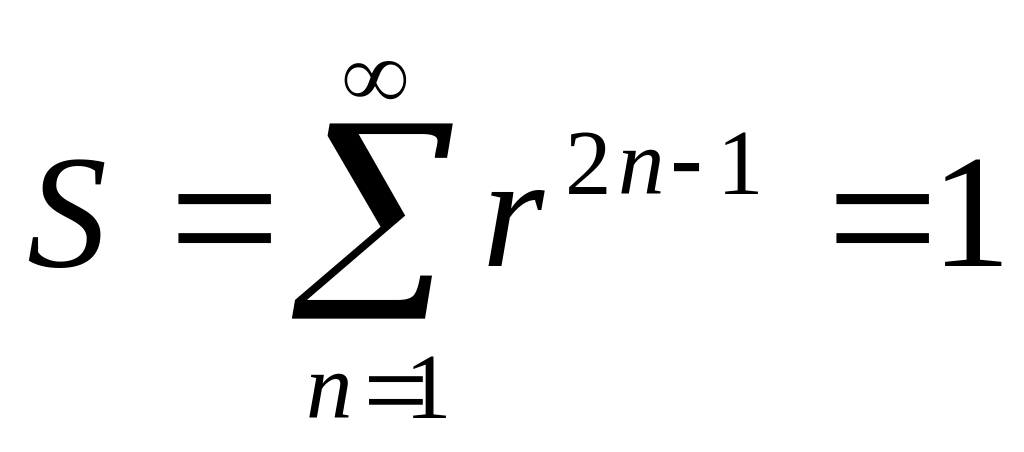, найти значение r.