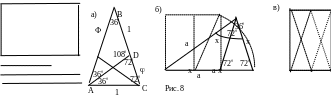- •Глава 1: Проценты 6
- •Глава 2: Арифметическая и геометрическая прогрессии 13
- •Глава 3: Геометрические построения в орнаментах и мозаиках 21
- •Глава 4: Пропорции 41
- •Глава 5: Немного о математике храмов Древней Руси (XI-xiIвв.) 57
- •Глава 7: Измерение фигур 76
- •Глава 8: Метод координат 87
- •Глава 9: Функции и графики 103
- •Глава 10: Конические сечения (коники). Кривые 2-го порядка 111
- •Глава 11: Непрерывность функции. Производная и кривизна 122
- •Глава 12: Интегральное исчисление 133
- •Глава 1 Проценты
- •Понятие процента
- •Абсолютная и относительная погрешность
- •Проценты вокруг нас
- •Применение процентов в банковской практике. Начисление процентов на вклад по простой и сложной схеме
- •Использование приближенных формул и таблиц, когда n велико
- •Сравнение сложной и простой схемы
- •Глава 2 Арифметическая и геометрическая прогрессии Метод полной индукции
- •Арифметические прогрессии
- •Геометрическая прогрессия
- •Бесконечные прогрессии
- •Примеры из финансовых расчетов
- •Глава 3 Геометрические построения в орнаментах и мозаиках Основные построения с помощью циркуля и линейки
- •Деление окружности на равные части с помощью циркуля и линейки
- •Построение логарифмической спирали
- •Построение узоров в круге на основе сеток
- •Движения на плоскости – перенос, поворот на угол , симметрии
- •Симметрия в орнаментах
- •Розетки
- •Бордюры
- •Решетки
- •Симметричные мозаики (паркеты)
- •Глава 4 Пропорции Понятие пропорции
- •Преобразование подобия. Гомотетия
- •Пропорция . Нормальный полиграфический лист
- •Метод «квадрата и его диагонали» в русской архитектуре. Восьмерики
- •Средние значения двух величин
- •Золотое сечение (деление отрезка в среднем и крайнем отношении)
- •Последовательность Фибоначчи и золотое сечение
- •Спираль Дюрера и «золотые» треугольники
- •"Золотая" пропорция и правильные многоугольники
- •«Золотая» прогрессия. «Золотые» модулеры
- •Производные «золота»
- •Глава 5 Немного о математике храмов Древней Руси (XI-xiIвв.)
- •Геометрические построения, применявшиеся древними мастерами
- •Некоторые стандарты планировки интерьера храма
- •Построение “золотого” плана циркулем и линейкой
- •Двухстолпный и бесстолпный храмы
- •План четырехстолпного храма
- •Глава 6 Размерение сооружений, имеющих "золотые" пропорции Модулер Корбюзье
- •Меры древней Руси
- •Глава 7 Измерение фигур
- •Измерение температуры
- •Тригонометрические функции
- •Решение треугольников
- •Площади плоских фигур
- •Многогранники
- •Правильные многогранники
- •Правильные пирамиды
- •Египетские пирамиды
- •Объемы фигур
- •Площади боковых поверхностей
- •Глава 8 Метод координат
- •Декартовы координаты
- •Векторы на плоскости
- •Полярная система координат
- •Связь между декартовыми координатами и полярными
- •Линии и их уравнения
- •Уравнение спирали Архимеда
- •Уравнение логарифмической спирали
- •Декартова система координат в трехмерном пространстве
- •Векторы в трехмерном пространстве
- •Сферические координаты
- •Сферические координаты в географии.
- •Орнаменты на сфере. Изогнутые крыши
- •Глава 9 Функции и графики Понятие функции
- •Четные и нечетные функции.
- •Периодические функции.
- •Монотонные функции.
- •Элементарные функции
- •Операции над графиками двух функций
- •Уравнение прямой на плоскости
- •Изменение уравнения линии при изменении системы координат
- •Глава 10 Конические сечения (коники). Кривые 2-го порядка Гипербола
- •Парабола
- •Эллипс как сжатая окружность. Каноническое уравнение эллипса
- •Построение овала с помощью циркуля и линейки. Характеристический прямоугольник. Фокусы эллипса
- •Эксцентриситет эллипса и параболы
- •Конические сечения
- •Кривые второго порядка
- •Проекции и конические сечения
- •Поверхности второго порядка в пространстве
- •Шары, эллипсоиды, конусы, цилиндры, параболоиды, гиперболоиды
- •Прямолинейные образующие
- •Глава 11 Непрерывность функции. Производная и кривизна Понятие предела
- •Непрерывность функции. Точки разрыва функции
- •Производная и ее геометрический смысл
- •Основные правила дифференцирования
- •Производные высших порядков
- •Роль производных в приближенных вычислениях
- •Производная и скорость изменения функции. Скачок производной
- •Знак производной и монотонность функции. Обращение производной в ноль
- •Выпуклость и вогнутость графика функции. Точки перегиба
- •Выпуклые, вогнутые и кровли с перегибом
- •Кривизна дуги
- •Глава 12 Интегральное исчисление Неопределенный интеграл
- •Основные методы интегрирования
- •Определенный интеграл. Задача о площади
- •Вычисление определенного интеграла
- •Основные свойства определенного интеграла.
- •Вычисление длин дуг.
- •Вычисление площади и длины дуги в полярных координатах
- •Вычисление длины окружности и площади круга и эллипса
- •Объем тела вращения
- •Площадь поверхности вращения
- •Ответы к задачам
- •Глава 1
- •Глава 2
- •Приложение
- •Изображение окружности и шара
- •Гирлянды (парабола)
- •Формулы
Спираль Дюрера и «золотые» треугольники
Обозначим
большую сторону "золотого"
прямоугольника через а,
а короткую через х.
Если от "золотого" прямоугольника
отсечь квадрат, остается прямоугольник,
большая сторона которого равна х,
а малая а-х
(рис. 7г). Отношение его сторон
![]() в силу соотношения
равно соотношению сторон
в силу соотношения
равно соотношению сторон
![]() в первоначальном прямоугольнике. То
есть новый прямоугольник подобен
первоначальному.
в первоначальном прямоугольнике. То
есть новый прямоугольник подобен
первоначальному.
Если отсечь от оставшегося прямоугольника квадрат, от оставшегося прямоугольника снова отсечь квадрат и т.д., то получится бесконечная последовательность квадратов, стороны которых уменьшаются в геометрической прогрессии. В пределе они заполнят весь первоначальный квадрат, сойдясь в точке, которая называется полюсом золотого прямоугольника. В этой точке пересекаются диагонали золотых прямоугольников. На рисунке 7г изображена спираль, метод построения которой предложен Дюрером, – в каждый квадрат «золотого» прямоугольника вписывается четверть круга. Эта спираль имеет бесконечное количество витков, закручиваясь вокруг полюса золотого прямоугольника. Такая спираль проста в построении и часто встречается в различных орнаментах. Она же может использоваться для приближенного построения спиралей, встречающихся в ионическом ордере.
В творениях и древних мастеров, и мастеров Возрождения часто просматриваются геометрические фигуры, пропорции которых связаны с "золотым" отношением. В "золотой" прямоугольник вписывается фасад Парфенона.
Из двух отрезков, длины которых относятся в «золотой» пропорции можно построить треугольники, которые часто служили основой для определения пропорций архитектурных и художественных произведений.
Замечательными
свойствами обладает равнобедренный
треугольник,
у которого отношение
длины боковой стороны к длине основания
равно Ф (или
отношение длины основания к длине
боковой стороны равно ).
Для того, чтобы построить такой
треугольник, построим "золотой"
прямоугольник, затем строим треугольник
по его 3 заданным сторонам. В качестве
основания берем короткую сторону
прямоугольника, а боковые стороны равны
длинной стороне прямоугольника (рис.
8а,б). Некоторые исследователи считают,
что этот треугольник лежит в основе
пропорции портрета Моны Лизы (рис. 8в).
Углы этого треугольника при основании
равны 72,
а угол, противолежащий основанию, равен
36.
Покажем, что отношение основания к
боковой стороне равнобедренного
треугольника, углы которого равны 72,
72
и 36,
есть "золотое" число .
Проведем биссектрису AD
угла А при основании (рис. 8а). Биссектриса
разобьет треугольник АВС на 2 треугольника
– ABD
и ADC.
Полученные треугольники равнобедренные.
У треугольника AВD
углы равны 36,
36
и 108.
Следовательно, BD=AD=AC.
У треугольника ADC
углы равны 72,
36
(половина угла в 72)
и ADC,
равный 180-72-36=72.
То есть, треугольник ADC
– равнобедренный и длина биссектрисы
угла при основании равна длине самого
основания. Он подобен первоначальному
треугольнику АВС (они имеют одинаковые
углы). Из подобия этих треугольников
следует, что:![]() .
Кроме того, ВС=BD+DC=AD+DC=AC+DC
и, следовательно, DC=ВС-АС.
Введем обозначения: АС=а,
АВ=k
и подставим эти значения в пропорцию:
.
Кроме того, ВС=BD+DC=AD+DC=AC+DC
и, следовательно, DC=ВС-АС.
Введем обозначения: АС=а,
АВ=k
и подставим эти значения в пропорцию:
![]() .
Обозначим
.
Обозначим
![]() ,
и решаем уравнение:
,
и решаем уравнение:
![]()
Таким образом, отношение длины боковой стороны треугольника, углы которого равны 72, 72 и 36, к длине основания есть "золотое" число Ф (положительный корень), отношение длины меньшей стороны к длине большей равно и конец биссектрисы делит боковую сторону в "золотом" отношении 1:=Ф:1 (рис. 8а).