Симметрия в орнаментах

Красота тесно связана с симметрией. Симметрия является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство. Наверно поэтому, начиная с древнейших времен, в произведениях искусства симметрия присутствует. Присутствует она и в природе (листья растений, снежинки, кристаллы, симметрия тела живого существа и т.д.) В силу важности предмета изучение законов симметрии обратилось в научную отрасль знания. Развитие теории с привлечением современного математического аппарата позволило создать описание всех возможных типов объектов, обладающих симметрией. Предметом теории симметрии является изучение квантования пространства: из пространства методами симметрии можно выделить равные части – кванты пространства. Кванты могут быть совмещаемы друг с другом с помощью переноса, вращения и отражения кванта. Мы коснемся только проблемы симметрии в орнаментах. Орнаменты представляют собой повторение с правильным пространственным ритмом элементов, имеющих вид некоторого рисунка. Следовательно, можно считать, что к шаблону, по которому создается орнамент, применяются операции движения. Это может быть простая операция переноса, последовательно выполняющаяся много раз, или для создания красивого симметричного рисунка может выполняться несколько движений – переносов, зеркальных отражений и поворотов.

Розетки

Самые простые ритмичные рисунки – розетки. Окружность делится на n равных частей. Орнамент, созданный в одном из секторов, n раз поворачивается на угол = . Поворачиваемый орнамент может иметь ось симметрии – биссектрису угла, образующего сектор. Можно описать схему орнамента. Точками отмечают центры поворота, стрелкой (или просто углом) указывается поворот, две стрелки, глядящие в разные стороны – отражение от оси между ними. На рисунке 11 приведена схема розетки, которая получается с помощью поворотов на 90 и 2-х узоров, построенных по этой схеме. Правее приведена схема получения розетки с помощью отражения и поворота и розетки, построенные по этой схеме. Сердце имеет ось симметрии, квантом является полусердце, оно отражается от оси симметрии, кроме того производится поворот на 90. Аналогичное строение имеют и еще две розетки, получающиеся с помощью отражения и поворота (8-ми-кратного и 5-ти-кратного).

Как эти, так и все последующие приведенные в этом руководстве рисунки, не являются художественными, а имеют целью только продемонстрировать в "абстрактной" форме методы построения симметричных узоров.

С обор в Модене

Церковь СанФранческо д’Ассизи (XIII в., Палермо)

Примеры симметричных узоров, являющихся прекрасными произведениями искусства, можно найти в книгах, посвященных архитектуре и интерьеру.

Бордюры

Бордюры – это ленточные орнаменты. Они располагаются вдоль центральной прямой l и обладают еще и шириной. Зеркальное отражение в ленточном орнаменте может быть продольным - от центральной прямой l, и поперечным – от прямой, перпендикулярной прямой l; продольное отражение может сочетаться с переносом на величину а вдоль центральной линии (продольное скользящее отражение). Поперечное отражение в сочетании с переносом на величину а

можно трактовать, как отражение от прямой, находящейся на расстоянии а/2. Может использоваться поворот на 180 вокруг точки и различные сочетания этих операций (рис. 12).

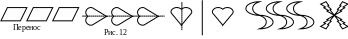
Естественно, при создании художественных орнаментов, кроме простых переносов-отражений, используются и различные приемы, лишающие рисунок монотонности. Но это уже не предмет математики.

Все способы, позволяющие внести симметрию в создаваемый объект, применяются и в архитектуре. Поворотная симметрия широко используется при постройке башен. Переносная - в фасадах зданий (яркий пример – дворец дожей в Венеции). Среди планов зданий и башен встречаются квадраты, прямоугольники, круги, правильные многоугольники (чаще всего восьмиугольники). Крайне редко встречается форма пятиугольника. Такую форму имеют здание Пентагона в Вашингтоне и Театр Советской Армии в Москве.