Деление окружности на равные части с помощью циркуля и линейки

С помощью циркуля и линейки можно разделить окружность не на любое число частей. Математики доказали, что на 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 17,…, 257,…частей разделить можно, на 7, 9, 11, 13, 14, … частей нельзя.

К сожалению, нет единого способа деления. Приведем самые главные.

1) Деление окружности на 6, 3, 12, 24, …, 32^k(k=0,1,2,3,…) равных частей.

Начинаем с деления окружности на 6 частей. Для этого тем же раствором циркуля, которым проводилась окружность, из любой точки окружности, как из центра, надо провести окружность. Затем повторить процедуру, взяв в качестве центра точку пересечения начальной и новой окружностей.

Чтобы поделить окружность на 3 части, надо поделить ее на 6 частей и взять точки через одну (рис. 5а). Чтобы поделить окружность на 12 частей, надо поделить ее на 6 частей и каждую дугу поделить пополам, далее процесс деления дуг пополам можно продолжать неограниченно.

Длина перпендикуляра, опущенного из центра окружности на сторону шестиугольника, является неплохим приближением для длины стороны семиугольника, вписанного в окружность (на рисунке 5а показан штриховкой). Длина перпендикуляра ≈0,866R, длина стороны семиугольника ≈0,868R – точность ≈2%.

2) Деление окружности на 2, 4, 8, 16,…, 2^k(k=1,2,3,…) равные части.

Разделить окружность на 2 части с помощью линейки можно, проведя прямую через центр окружности. Но можно от любой точки окружности 3 раза отложить радиус круга. Начальная и конечная точки делят окружность пополам (через них можно провести диаметр - рис. 5а). Чтобы поделить окружность на 4 части, надо поделить пополам полученные дуги. Последовательное выполнение деления полученных дуг пополам обеспечивает деление окружности на 8, 16 и т.д. частей.

3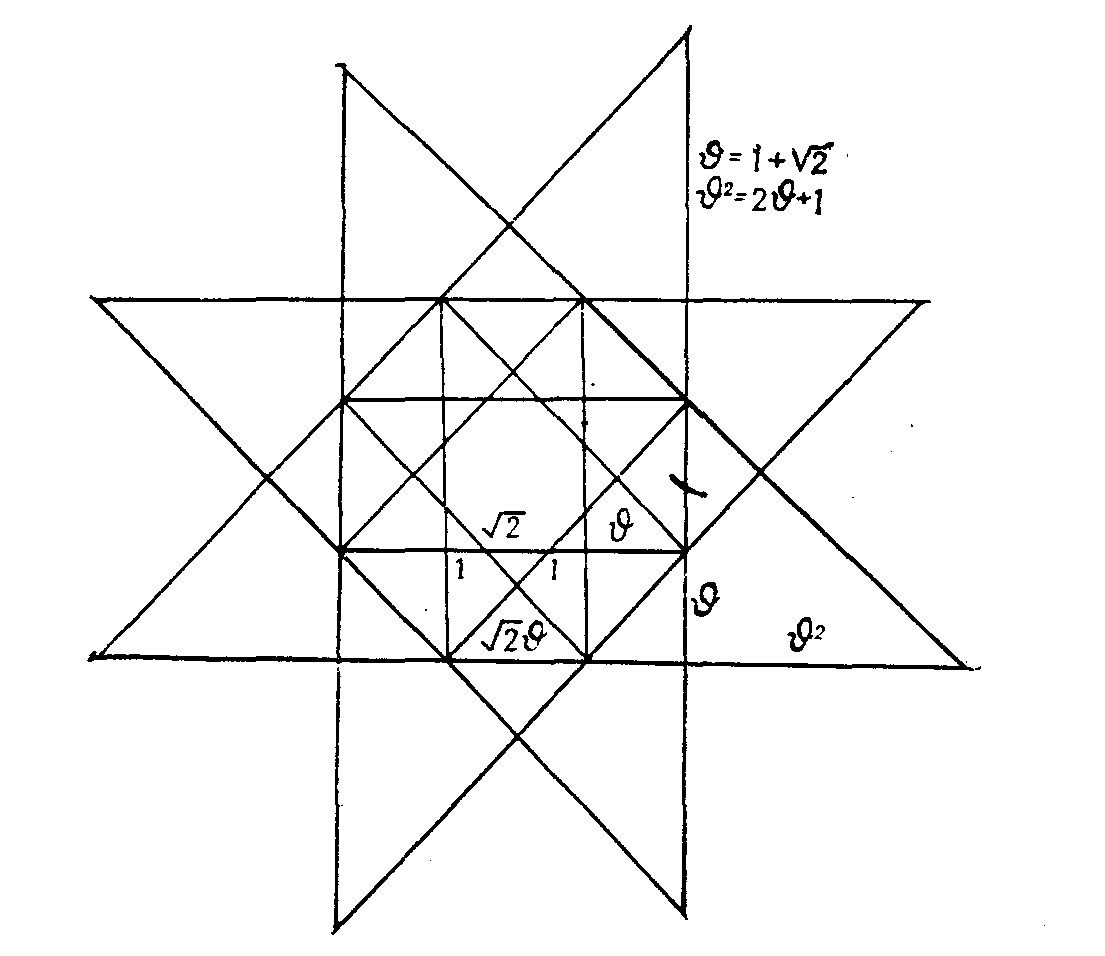 ) Деление окружности на 5 частей.

Принятый в черчении способ построения использует соотношение между стороной правильного десятиугольника (а₁₀) и правильного пятиугольника (а₅) - a₅²=R²+a₁₀². Выполняется построение следующим образом. Проведем 2 перпендикулярные прямые через центр окружности О. А и В – точки их пересечения с окружностью. Из точки А, как из центра, проведем окружность того же радиуса (найдем середину отрезка АО – точку С). Из середины отрезка АО точки С проведем еще одну окружность радиуса СВ. Отрезок ВЕ – равен стороне пятиугольника, ОЕ – десятиугольника (рис. 5б).

Можно делить окружность на 5 и 10 частей способом, изображенным на рисунке 5в. Отрезок ВС - сторона пятиугольника, АС - десятиугольника. О замечательных свойствах пятиугольника и десятиугольника и о том, почему верен способ построения, приведенный на рисунке 5в, мы расскажем в следующей главе.

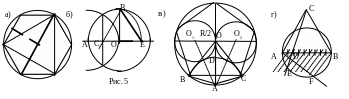
М едресеКукельдаш (XVIв., Ташкент)

Рисунок 5г демонстрирует прием приближенного геомет-рического решения задачи о делении окружности на любое число частей. Пусть, например, требуется разделить данную окружность на 7 равных частей. Построим на диаметре окружности АВ равносторонний треугольник АВС и разделим диаметр АВ точкой D в отношении AD:AB=2:7 (в общем случае 2:n). Для этого надо провести вспомогательную прямую, на ней отложить n+2 одинаковых отрезка , крайнюю точку соединить с точкой В и через вторую точку провести прямую, параллельную прямой BF. Проведем прямую DC до пересечения с окружностью. Дуга АЕ будет составлять 7-ую часть окружности (в общем случае n-ю). Этот метод при n<11 дает погрешность не более 1%.

Алгоритмы деления окружности на равные части можно использовать, например, для построения опорных точек спиралей - спирали Архимеда, названной так в честь великого древнегреческого ученого Архимеда (III в. до н.э.), впервые изучившего эту линию, и логарифмической спирали.

Построение спирали Архимеда

Спираль Архимеда - это кривая, которую описывает точка, движущаяся с постоянной скоростью v по лучу, который вращается около полюса О с постоянной угловой скоростью .

Геометрически спираль Архимеда можно описать так: расстояние  от точки М до полюса О (=ОМ) пропорционально углу поворота  луча ОМ (рис 6).

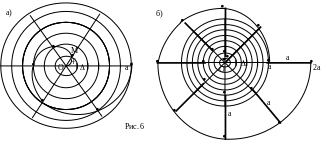
Повороту луча ОМ из любого его положения на одно и то же значение  соответствует одно и то же приращение длины радиуса-вектора =ОМ на . Полному обороту луча на 2 соответствует одно и то же смещение вдоль луча на величину а. Отрезок а называется шагом архимедовой спирали (рис. 6б). Если вращать луч ОМ против часовой стрелки, получается правая спираль, если по часовой стрелке, то левая.

Построим опорные точки для графика спирали Архимеда. Проведем окружность радиуса а, разделим ее на n частей, соединим концы дуг с центром окружности О. Разделим радиус окружности на n равных частей. Пусть длина одной части равна . Первой опорной точкой будет центр окружности О. Если повернуть горизонтальный радиус на угол, равный =2/n, то расстояние от точки спирали до точки О станет равным . Таким образом, чтобы получить вторую опорную точку, надо на радиусе, имеющим угол поворота 2/n, отложить отрезок длины . Чтобы получить третью точку, надо на радиусе, соответствующем углу поворота =22/n, отложить отрезок длины 2, на следующем за ним радиусе отложить 3 и т.д. Т.е. последовательность расстояний от 1-ой, 2-ой, 3-ьей и т.д. опорной точки до начала координат суть арифметическая прогрессия. Через n шагов мы придем в точку, лежащую на луче, с которого мы начинали процесс, отстоящую от центра на расстояние n=a. Далее процесс продолжается по этой же схеме - c каждым поворотом луча ОМ на угол 2/n будем увеличивать расстояние точки от центра О на величину . Эта схема соответствует тому, что =ОМ пропорционально углу поворота , при этом на каждом луче расстояние между точками разных витков спирали постоянно и равно а - шагу спирали. На рисунке 6 построены опорные точки для 2-х спиралей - левая строилась делением окружности и начального радиуса на 6 частей, спираль на правом графике имеет шаг спирали в полтора раза меньше, количество опорных точек не 6, а 8. Взятые нами значения n=6 (на левом чертеже) и n=8 (на правом) дают очень небольшое количество опорных точек графика. Мы лишь продемонстрировали принцип построения.

Этот же принцип применяется, когда надо построить кусок спирали.

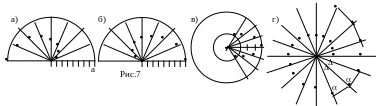
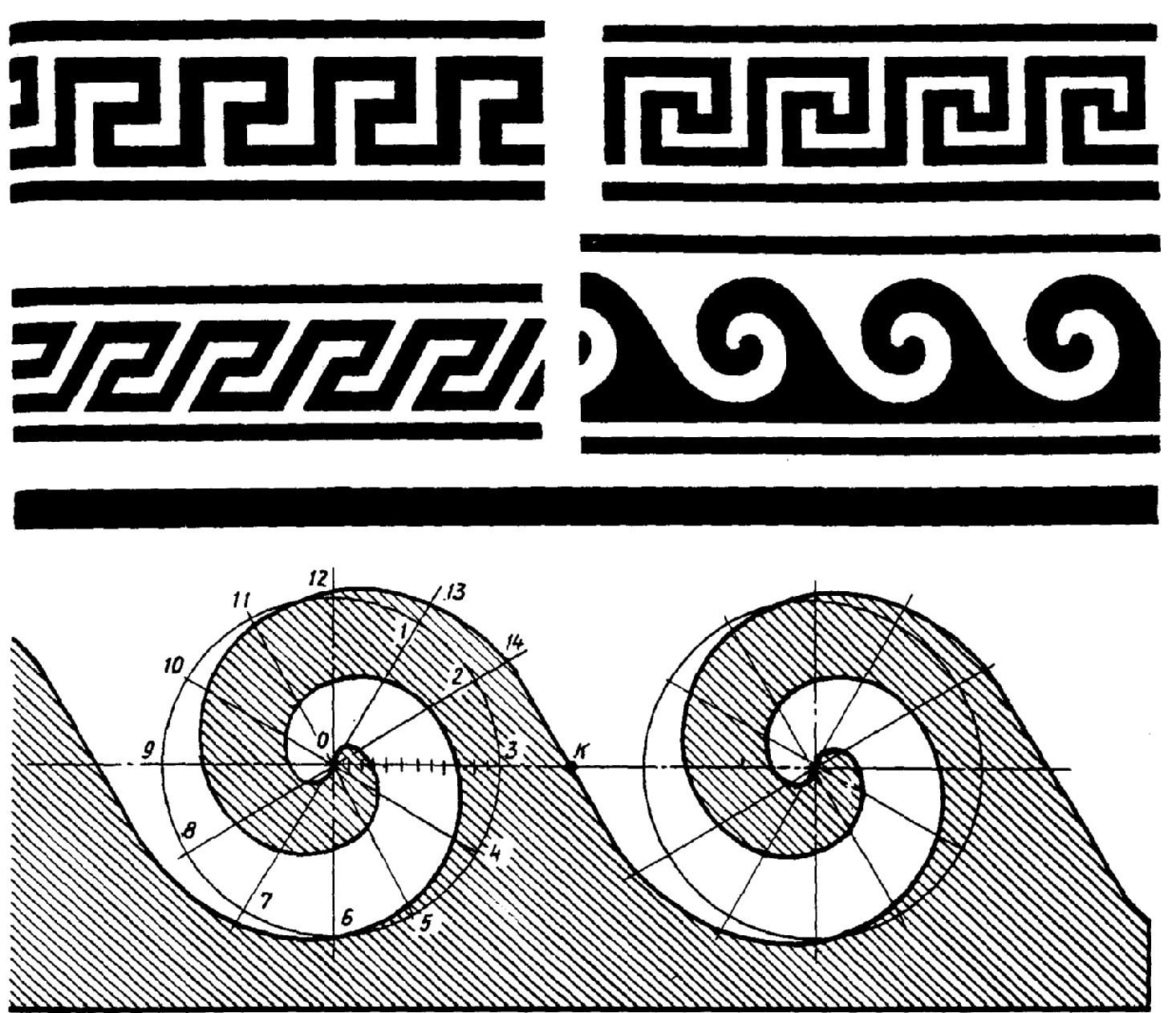
Если мы хотим построить n опорных точек для куска спирали Архимеда, для которого угол меняется лишь на величину  (например, ), а длина радиуса-вектора на величину а, надо провести дугу окружности, центральный угол которой равен  (для = - полуокружность), поделить начальный отрезок длины а на n равных частей и дугу окружности на n равных дуг и построить опорные точки, как показано на рисунках 7а,б,в.

Меандр

Узоры из дуг спиралей очень красивы. Такая розетка украшает, например, купол Павильона Катальной Горки в Ораниенбауме. В Оружейной плате Московского Кремля хранится щит Мстиславского, украшенный красивым узором из спиралей. Орнамент из дуг часто используется для украшения сервизов, блюд и т.д.

Щит Ф.И. Мстиславского (XVIв., персидский мастер)

К упол павильона Катальная горка (XVIII в., Ораниенбаум)