Физика

30. Движение заряж. Частицы в электрическом и магнитных полях

Электрические и магнитные поля действуют на движущиеся заряженные частицы с известной силой. Поэтому эти поля могут использоваться для управления движением заряженных частиц.  Описание движения заряженной частицы проводится на основании второго закона Ньютона, уравнение которого имеет вид

Ma=qE+qV*B

где qE − сила, действующая на частицу с электрическим зарядом q со стороны электрического поля; qv x B − сила Лоренца, действующая на частицу со стороны магнитного поля. В общем случае напряженность электрического поля E и индукция магнитного поля B могут зависеть от координат (в неоднородных полях) и времени (в нестационарных полях). Для однозначного решения уравнения его необходимо дополнить начальными условиями: положением частицы ro и скоростью vo в некоторый момент времени to. При описании распространения потоков частиц в некоторых случаях необходимо также учитывать взаимодействия частиц между собой, или принимать во внимание зависимость характеристик полей от положения и скоростей других частиц. Наконец, при записи уравнения принято, что частицы движутся в вакууме, где отсутствуют силы сопротивления среды. Движение частиц в средах, обладающих сопротивлением, описываются в рамках уравнений для электрического тока. При движении частиц в электромагнитном поле, как правило, пренебрегают действием силы тяжести, которая обычно значительно меньше электромагнитных сил.

31. Закон Био-Савара-Лапласа для расчета магнитных полей токов

Магнитное поле постоянных токов различной формы исследовалось французскими учеными Ж. Био (1774—1862) и Ф. Саваром (1791—1841). Результаты их опытов были обобщены французским ученым П. Лапласом. Закон Био-Савара-Лапласа для проводника с током I, элемент dl которого создает в некоторой точке А (рис. 1) индукцию поля dB, равен

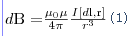
где dl - вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током, r - радиус-вектор, который проведен из элемента dl проводника в точку А поля, r - модуль радиуса-вектора r. Направление dB перпендикулярно dl и r, т. е. перпендикулярно плоскости, в которой они лежат, и совпадает с направлением касательной к линии магнитной индукции. Это направление может быть найдено по правилу правого винта: направление вращения головки винта дает направление dB, если поступательное движение винта совпадает с направлением тока в элементе.

Модуль вектора dB задается выражением

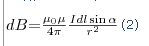
где α — угол между векторами dl и r. Аналогично электрическому, для магнитного поля выполняется принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности:

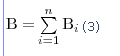
32, Явление электромагнитной индукции. Правило Ленца

Явление электромагнитной индукции было открыто выдающимся английским физиком М. Фарадеем в 1831 г. Оно заключается в возникновении электрического тока в замкнутом проводящем контуре при изменении во времени магнитного потока, пронизывающего контур.

Магнитным потоком Φ через площадь S контура называют величину Φ = B · S · cos α,

где B – модуль вектора магнитной индукции, α – угол между вектором и нормалью к плоскости контура

Определение магнитного потока нетрудно обобщить на случай неоднородного магнитного поля и неплоского контура. Единица магнитного потока в системе СИ называется вебером (Вб). Магнитный поток, равный 1 Вб, создается магнитным полем с индукцией 1 Тл, пронизывающим по направлению нормали плоский контур площадью 1 м2: 1 Вб = 1 Тл · 1 м2.

Фарадей экспериментально установил, что при изменении магнитного потока в проводящем контуре возникает ЭДС индукции инд, равная скорости изменения магнитного потока через поверхность, ограниченную контуром, взятой со знаком минус:

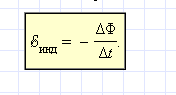
Эта формула носит название закона Фарадея.

Опыт показывает, что индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток. Это утверждение, сформулированное в 1833 г., называется правилом Ленца.

Правило Ленца отражает тот экспериментальный факт, что инд и дельта F/дельта v всегда имеют противоположные знаки (знак «минус» в формуле Фарадея). Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.