10.8.1. Замечания по интегрированию дифференциальных уравнений изгиба жёсткой пластинки

Точное решение уравнений (10.11) и (10.14) вызывает большие трудности. Поэтому при решении практических задач применя­ют приближённые методы.

Одним ив наиболее распространённых является метод И. Г. Бубнова и Б.Г.Галеркина, который основан на принципе возможных пе­ремещений.

Согласно принципу возможных перемещений реальное равновесное состояние упругой системы характеризуется равенством нулю суммы работ всех внешних и внутренних сил на любом кинематически возможном перемещении её точек.

Рассмотрим метод Бубнова-Галёркина на примере решения зада­чи по определению максимального прогиба и наибольших нормальных напряжений прямоугольной пластинки, нагруженной поперечной на­грузкой постоянной интенсивности р = const (рис. 10.4). Пластинка шарнирно опёрта по всем четырём краям.

Для приближённого решения выберем функцию прогибов в виде одночлена

, (10.15)

которая удовлетворяет граничным условиям.

Исходное дифференциальное уравнение

можно представить в виде

z = р,

где Z - равнодействующая погонных усилий, действующих по граням элемента.

Если взять элемент пластинки размером dxdy , то силы pdxdy и Zdxdy - являются соответственно равнодействующими внешних и внутренних сил элемента. Первая направлена вертикально вниз, вторая - вверх.

Дадим пластинке возможное перемещение в виде малого проги­ба

Тогда согласно принципу возможных перемещений

,

или

С учётом выражения оператора и производных имеем:

но

;

.

Следовательно,

,

или

.

Для квадратной пластинки, а = b

.

Точное решение для квадратной пластинки при μ = 0,3

отличается от приближённого всего на 2,5%..

Формулы для определения наибольших значений прогибов, а также нормальных напряжений в центре пластинки можно представить в виде:

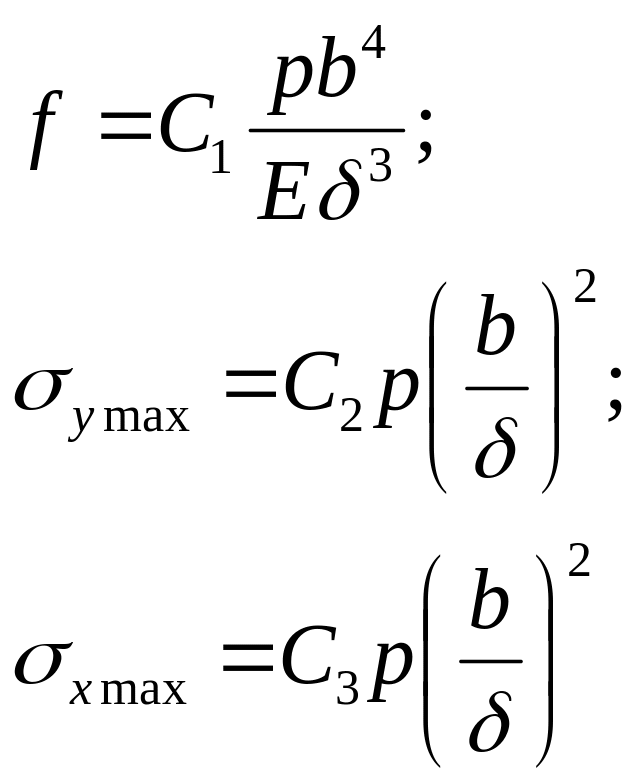(10.16)

где С₁, С₂, С₃ - коэффициенты полученные в результате точного решения для заданного отношений сторон а/b пластинки.

Для шарнирно опёртой пластинки при р = соnst имеем:

а/b	С1	С2	С3
1	0,0433	0,2870	0,2870
1,2	0,0616	0,3760	0,3010
1,4	0,0770	0,4520	0,3040
1,6	0,0906	0,5170	0,2960
1,8	0,1017	0,5690	0,2870
2,0	0,1106	0,6100	0,278O
3,0	0,1336	0,7130	0,2420.
4,0	0,1400	0,7410	0,2300
	0,1422	0,7500	0,2250

Пример. Определить наибольшее напряжение и прогиб прямоугольной пластинки, опёртой шарнирно по всем четырём сторонам и нагруженной равномерно распределённой нагрузкой р.

Материал пластинки – дюраль Д16-АТ с модулем упругости Е = 710⁵ даН/см². Размеры: а = 24 см, b = 20 см,  = 0,4 см.

Нагрузка р = 0,4 даН/см².

р е ш е н и е

Определим отношение сторон пластинки

a/b = 24/20 = 1,2

Из таблицы получим С₁ = 0.0616 и С₂ = 0,3760. Тогда

Так как С₂, > С₃, то σ_уmах - наибольшее напряжение.