9.7.3. Влияние характера опирания пластинок на их граничные условия

Характер опирания пластинок определяет их граничные условия. Taк, жёсткое защемление пластинки по краю обеспечива­ется двухрядным заклепочным швом при достаточно жёстких подкрепляющих рёбрах (рис.10.15, а ).

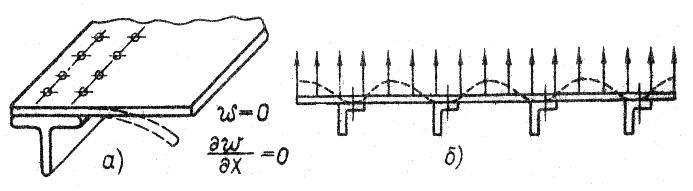
Рис.10.15. Влияние характера опирания пластинок на их граничные условия

Длинная неразрезная пластинка, опертая на несколько ребер и нагруженная силами, направленными в одну сторону (рис. 10.15,б), и при однорядном заклепочном шве работает как защемлённая. Её сечения над опорами не поворачиваются вследствие симметрии изогнутой поверхности.

Однорядный заклёпочный шов изолированной пластинки слабо сопротивляется повороту края пластинки, поэтому такое опирание можно считать шарнирным,

9. 8. Дифференциальное уравнение продольно- поперечного изгиба жёсткой пластинки

Если жёсткая прямоугольная пластинка наряду с поперечной нагрузкой р нагружена в срединной поверхности внешними погон­ными нормальными n_х = σ_х , N_y = σ_х и касательными q =  усилиями (рис. 10.16), то её дифференциальное уравнение продольно-поперечного изгиба имеет вид:

(10.14)

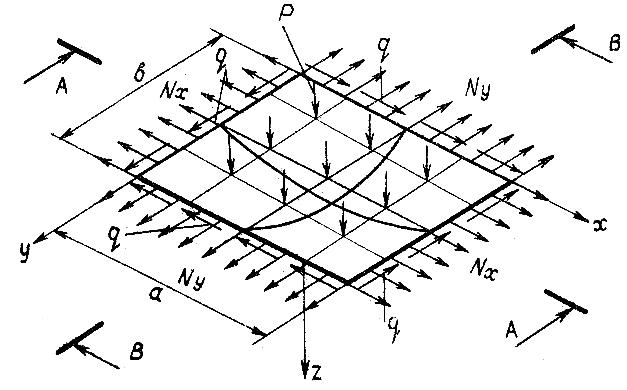
Рис. 10.16. Деформации жёсткой прямоугольной пластинки при нагружении её поперечной нагрузкой р, внешними погон­ными нормальными усилиями в срединной поверхности n_х = σ_х , N_y = σ_х и касательными усилиями q = 

Вывод этого уравнения приведен в Приложении 1.

Замечания по интегрированию дифференциальных уравнений изгиба жёсткой пластинки приведены в Приложении 2

ВОПРОСЫ

1. Дайте определения понятиям: прямоугольная пластинка, срединная плоскость пластинки, изогнутая срединная поверхность пластинки.

2. Какую нагрузку способна воспринимать пластинка?

3. В каком случае пластинка может воспринимать распределённую нагрузку, направленную перпендикулярно к плоскости пластинки?

4. Можно ли пластинку непосредственно нагружать сосредоточенными силами?

5. Как работает пластинка в составе конструкции?

6. На какие классы делятся пластинки? Кокой принцип этой классификации?

7. Что такое цилиндрический изгиб пластинки?

8. Какие параметры входят в формулу для определения цилиндрической жёсткости пластинки?

9. Какие параметры входят в дифференциальное уравнение изогнутой жесткой пластинки при поперечном изгибе?

10. Какие возможны граничные условия по краям пластинки? От чего они зависят?

11. Какие параметры входят в дифференциальное уравнение продольно-поперечного изгиба жесткой пластинки?

Приложение 1.

ВЫВОД Дифференциального уравнения продольно- поперечного изгиба жёсткой пластинки

Если жёсткая прямоугольная пластинка наряду с поперечной нагрузкой р нагружена в срединной поверхности внешними погон­ными нормальными n_х = σ_х , N_y = σ_х и касательными q =  усилиями (рис. 10.16), то её дифференциальное уравнение продольно-поперечного изгиба имеет вид:

(10.14)

Рис. 10.16. Деформации жёсткой прямоугольной пластинки при нагружении её поперечной нагрузкой р, внешними погон­ными нормальными усилиями в срединной поверхности n_х = σ_х , N_y = σ_х и касательными усилиями q = 

Для вывода этого уравнения рассмотрим в сечении А-А пластинки (рис. 10.16) изогнутую ось элемента dxdy (рис. 10.17).

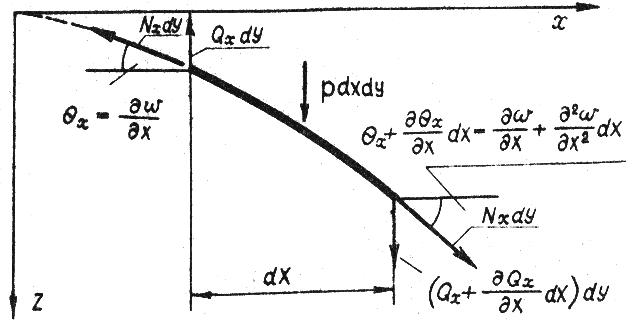
Рис. 10.17. Изогнутая ось элемента dxdy в сечении пластинки А-А

Будем считать, что усилия, действующие по граням dy элемен­та, приложены к его оси. Проектируя эти усилия на ось z, получим

Рассматривая элемент в сечении В-В (рис. 10.16), увидим, что составляющая в направлении оси Z от усилий, действующих по граням dx элемента, равна

.

Кроме усилий N_х и N_y в срединной поверхности элемента действуют усилия q, которые вследствие кручения также созда­ют составляющую в направлении оси Z

.

Суммирование проекций всех сил на ось Z с учётом нагрузки рdхdy приводит к равенству

.

Подставив в это равенство значения q_х и q_у (10.9), получим приведенное выше уравнение (9.14).

Приложение 2