1 0. 6. Дифференциальное уравнение изгиба жёсткой пластинки

Дифференциальное уравнение изгиба жёсткой пластинки можно получить, рассматривая равно-весие элемента dхdу (рис.10.12), нагру-женного распределён-ной нагрузкой р и уравновешенного внут-ренними усилиями по боковым граням.

При этом следует учитывать изменение внутренних усилий

Рис. 9.12. Элемент жёсткой пластинки. из-за изменения ко­ординат граней.

Например, по грани определяемой коор­динатой х действует изгибающий момент M_xdy, а по грани dy, определяемой координатой х + dх, -момент

Уравнение моментов относительно оси y всех усилий, действующих на элемент, имеет вид

Пренебрегая малыми более высокого порядка, получим

(а)

Из условия равновесия элемента относительно оси X следует

, (б)

а из уравнения проекций на вертикальную ось Z

(в)

Уравнения (а), (б), (в) являются обобщением дифференциальных зависимостей dМ/dх = q и dq/dх = р для балок.

Выразим поперечные сил» Q_x и q_у через производные от прогибов w, используя соотношения (10.7) и (10.8) и равенст­во k_хy = k_yх для бесконечно малого элемента

(10.9)

Подставив (9.9) в уравнение (в), получим дифференциальное уравнение изогнутой жесткой пластинки при поперечном изгибе

. (10.10)

Применив оператор

,

уравнение (9.10) можно переписать в виде

(10.11)

Интегрируя уравнение (10.11) при определённых граничных ус­ловиях, определяют прогибы w пластинки, как функцию координат х и у. Далее по формулам (10.7), (10.8) и (10.9) находят уси­лия в сечениях пластинки, а по (10.2) - напряжения.

9.7. Граничные условия

При интегрировании уравнения (10.11) должны выполняться гра­ничные условия по краям пластинки, зависящие от характера её крепления.

Рассмотрим граничные условия, представляющие наибольший практический интерес.

9.7.1. Шарнирно опёртый край

Для любой точки края (х = 0) при шарнирном опирании (рис. 10.13,а) должны выполняться следу­ющие условия:

прогиб w_х=0 = 0; (а)

изгибающий момент М_х_х=0 =0. (б)

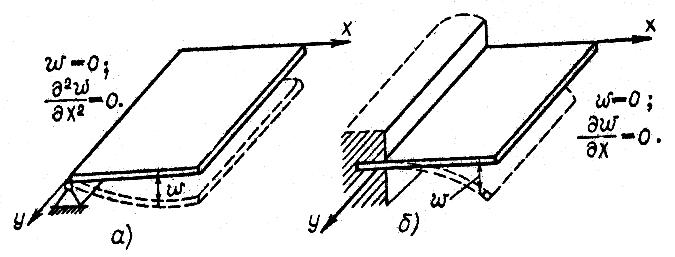
Рис. 10.13. Граничные условия при различных видах опирания пластинки

Так как и всем точкам края соответствует постоянный прогиб w = 0 ( ), то условию (б) тождественно выражение

Окончательно граничными условиями шарнирно опёртого края пластинки ( х = 0 ) будут:

; (10.12)

Е сли пластинка шарнирно опёрта по всем четырём краям, гра­ничные условия запишутся в виде:

9.7.2. Жёстко защемлённый край

Для любой точ­ки (рис.10.13, б), рассматриваемого края (х = 0) должны равняться нулю:

- прогиб w;

- угол наклона касательной к изогнутому волокну, параллель­ному оси х .

Таким образом, для защемлённого края получаем условия:

(10.13)

Если пластинка жёстко защемлена по всем четырём краям, гра­ничные условия будут иметь вид:

Условное обозначение шарнирного опирания и жёсткого защем­ления пластинки по четырём краям представлено соответственно на рис 10.14, а, б.

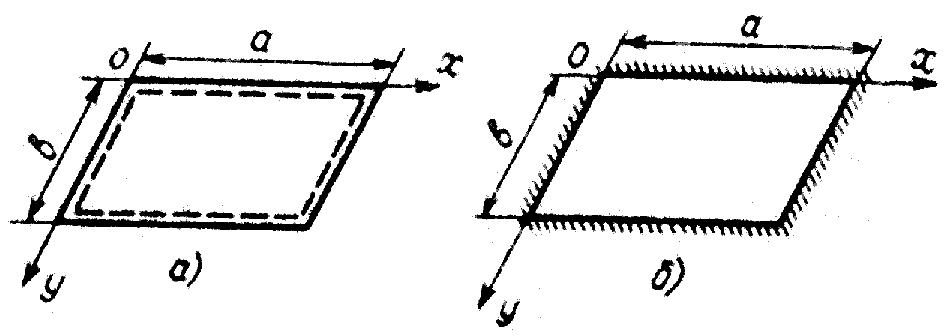
Рис. 10.14. Условное обозначение шарнирного опирания и жёсткого защем­ления пластинки по четырём краям