1.1 Движение тела может быть как поступательным так и вращательным. В этом случае тело представляется в виде системы жестко связанных между собой материальных точек.

При поступательном движение любая прямая, проведенная в теле , перемещается параллельно самой се­бе. По форме траектории поступательное движение может быть прямолинейным и криволинейным. При поступательном движении все точки твердого тела за один и тот же промежуток времени совершают равные по величине и направлению перемещения (Рис1). Следовательно, скорости и ускорения всех точек тела в любой момент времени также одинаковы.

Для описания поступательного движения достаточно определить движение одной точки.

Вращательным движением твёрдого тела вокруг неподвижной оси называется такое движение, при котором все точки тела движутся _по окружностям, центры которых лежат на одной прямой (ось вращения)(Рис2).Ось вращения может проходить через тело или лежать за его пределами. Если ось вращения проходит сквозь тело, то точки, лежащие на оси, при вращении тела остаются в покое. Точки твёрдого тела, находящиеся на разных расстояниях от оси вращения за одинаковые промежутки времени проходят различные расстояния и следовательно имеют различные линейные скорости

1.2 Для описания вращательного движения тел вводят понятия момента инерции и момента силы. Момент инерции материальной точки относительно оси вращения есть скалярная величина, равная где m - масса движущейся материальной точки, к кратчайший расстояние от оси вращения до материальной точки (рис.7).

Моментом инерции системы из n материальных точек относительно оси вращения есть сумма моментов инерций отделённых материальных точек относительно этой же оси .Моментом инерции dJi некоторого элемента массы твёрдого тела относительно оси вращения называется величина, численно равная произведению массы элемента на квадрат расстояния от него до оси вращения . I=mr²

Момент инерции характеризует инерционные свойства вращающихся тел. Чем больше момент инерции тела, тем труднее изменить его угловую скорость. Момент инерции во вращательном движении аналогичен массе тела в поступательном движении. Момент инерции тела относительно некоторой оси зависит от распределения его массы относительно оси вращения (рис.8)

Моменты инерции (J) тел простой формы относительно оси, проходящей через их центры инерции С, приведены в справочни-ках.

Момент инерции тела относительно оси, не проходящей через его центр инерции опреде- ляется согласно теоремы Штейнера :

Момент инерции тела относительно произвольной оси равен сумме момента инерции этого тела относительно оси, проходящей, через его центр инерции параллельно рассматриваемой оси и произведения массы тела m на квадрат расстояния d между осями. I=I₀+md²

1.3 Работа это скалярная физическая величина численно равная А=F*S*cosf=Fs*S Сила перпендикулярна перемеш.

Механическая энергия это кол. характеристика мех. дв. Материи и ее изменения. Мех. энергия состоит из двух энергии Eк и Eп Е=Ек+Еп

Кинетическая энергия это энергия движения тел.

Кинетическая энергия поступательного дв. Eк=mv²/2

Кинетическая энергия вращ. дв. Eк=mR²w²/2 . Eк=Iw²/2 v=wR

энергии поступательного движения и

энергии вращения Eк=mv²/2+ Iw²/2

Моментом силы относительно неподвижной точки О называется физическая величина М, определяемая векторным произведением радиуса-вектора г, проведенного из точки О в точку

Л приложения силы, на силу F M=r*F: r=sinL=L: M=FL

Моментом силы относительно неподвижной оси z называется скалярная величина М,, равная проекции на эту ось вектора Л/момента силы, определенного относительно произвольной точки О данной оси z (рис. 28). Значение момента М, не зависит от выбора положения точки О на оси z.

Работа 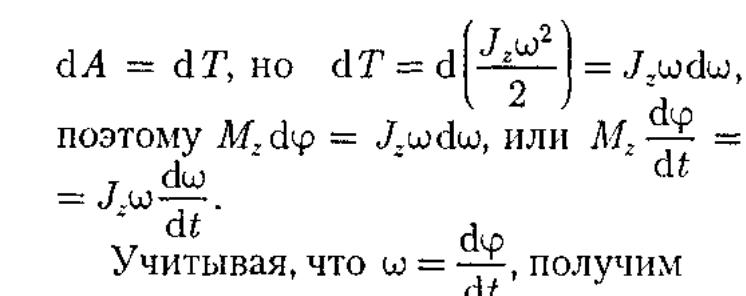при вращении тела идет на увеличение его кинетической энергии:

Е-угловое ускорение, J-момент инерции тела относительно оси Z