9. Производные и интегралы

Операции дифференцирования и интегрирования в системе MathCAD достаточно просто выполнить с помощью соответствующих операторов. Здесь рассматриваются только численные операции, возможности символьного дифференцирования и интегрирования не излагаются.

9.1 Операторы дифференцирования и интегрирования

Математические выражения в MathCAD могут содержать операторы дифференцирования и интегрирования. Их удобно вводить с помощью панели инструментов Calculus (таблица 9.1). Причем операции дифференцирования и интегрирования обозначаются при помощи традиционных обозначений.

Табл. 9.1 – Операторы дифференцирования и интегрирования

Оператор	Назначение оператора	Панель инструментов
	Возвращает производную f(x) в точке x
	Возвращает n-ю производную f(x) в точке x
	Возвращает определенный интеграл от f(x) c пределами интегрирования от a до b
Примечание  Производные высшего порядка рассчитываются до 5-го включительно

При этом функция f(x), значения a, b и x должны быть определены заранее. Кроме того, функция f(x) может быть функцией многих переменных.

9.2 Дифференцирование

В

Рис. 9.1 – Пример применения

оператора дифференцирования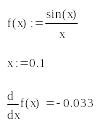

ычислительный процессор MathCAD обеспечивает вычисление производной с точностью до 7-8-го знака после запятой.

Дифференцирование в точке

Для того чтобы продифференцировать некоторую функцию f(x) в некоторой точке необходимо (рисунок 9.1):

1. определить точку, в которой вычисляется производная;

2. ввести оператор дифференцирования, заполнить соответствующие маркеры;

3. ввести оператор численного вывода результата – знак =.

При дифференцировании в MathCAD обычно не возникает сложных проблем. Исключение составляют функции, которые дифференцируются в окрестности сингулярной точки, например, в точке x=0 для функции f(x)=1/x. Проверить это вы можете самостоятельно.

Производные высших порядков

В

Рис. 9.2 – Оператор дифференцирования второго порядка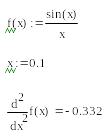

MathCAD можно вычислять производные до 5-го порядка. Для этого следует проделать те же операции, что и в предыдущем случае производной 1-го порядка. На рисунке 9.2 приведен соответствующий пример.

Частные производные

Можно вычислять частные производные функций со многими переменными. Для этого по умолчанию используются те же операторы дифференцирования (см. таблицу 9.1). Это несколько отличается от классических обозначений в математике. При желании форму записи можно изменить, но мы этим заниматься не будем. В качестве примера на рисунке 9.3 приведена программа вычисления градиента функции двух переменных с использованием частных производных.

Рис. 9.3 – Построение векторного поля градиента заданной функции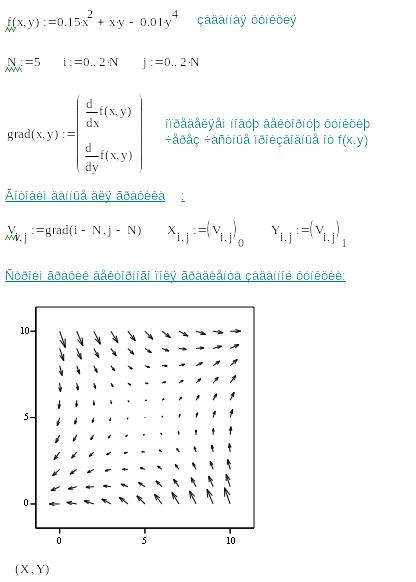

Математическую интерпретацию полученных результатов вы можете дать, используя векторный анализ.

9.3 Интегрирование

Численное интегрирование – достаточно простая вычислительная операция. Оно реализовано в виде соответствующего оператора MathCAD (см. таблицу 9.1). Результатом численного интегрирования является некоторое число – значение определенного интеграла. Задача нахождения неопределенного интеграла решается с помощью символьного процессора. Здесь эти вопросы не рассматриваются.