ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

АЛТАЙСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Математический факультет

Кафедра математического анализа

ЭЛЕМЕНТЫ ТЕНЗОРНОГО ИСЧИСЛЕНИЯ

(практикум)

Издательство Алтайского государственного университета

Барнаул 2010

Составители:

профессор АлтГУ М.А. Чешкова

Указания предназначены для практических занятий со студентами 2 и 3 курсов математического факультета. Для каждого занятия приведен необходимый теоретический материал, иллюстрирующие примеры, сформулированы задачи для домашнего задания.

План УМД 2010 г.

Подписано в печать г. Формат 6090/16.

Бумага газетная. Печать офсетная.

Уч.-изд. л. 1,6. Тираж 100 экз. Заказ .

Типография Алтайского государственного университета:

656049, Барнаул, ул. Димитрова, 66

ЛИНЕЙНЫЕ И ПОЛИЛИНЕЙНЫЕ ОТОБРАЖЕНИЯ

Соглашение о суммировании

В выражении полагаем, что по индексу , повторяющемуся дважды и стоящему на разных уровнях (один вверху, как у , один внизу, как у ) производится суммирование от до , где . Индекс называется индексом суммирования. Он может быть заменен любой буквой. Те индексы, которые не суммируются, называются свободными.

Примеры:

,

,

– индексы суммирования,

– свободный.

Линейные отображения

Пусть – векторные пространства.

Определение 1. Отображение называется линейным, если

1) , ,

2) , .

Определение 2. Отображение полилинейно, если

1) ,

2) ,

Теорема 1. Множество полилинейных отображений относительно операций

,

образует векторное пространство .

Теорема 2. , где ,.

Пример 1:

, , ,

,

– линейное отображение.

Полилинейные формы

Определение 3. Полилинейное отображение называется -формой; при – линейной формой.

Определение 4. Векторное пространство линейных на форм называется сопряженным, или дуальным, обозначается .

Определение 5. Базис называется дуальным к базису , если

Пример 2. Определить .

Решение: .

Пример 3. Проверить, является ли функция билинейной формой.

Решение:

,

.

,

– нет.

Пусть тогда где – координаты -формы .

Контрольные вопросы

1. Расписать .

2. Определить , где символ Кронекера.

3. Сколько слагаемых в суммах ?

4. Упростить .

5. Определить .

6. Выделить линейные формы ,

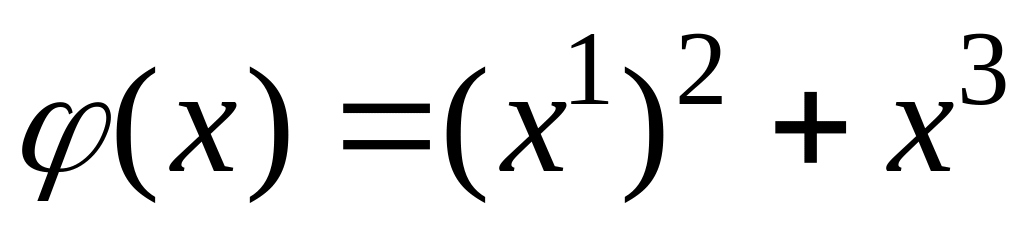7. Выделить билинейные формы , .

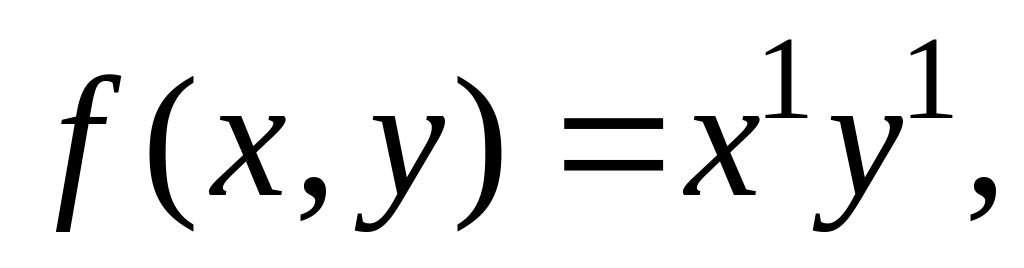
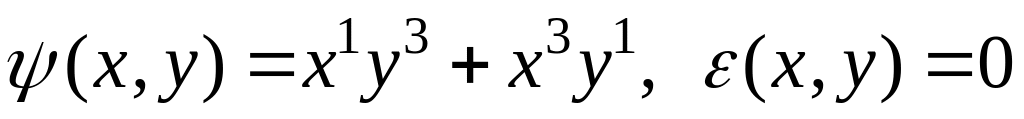8. Написать разложение линейной формы по базису 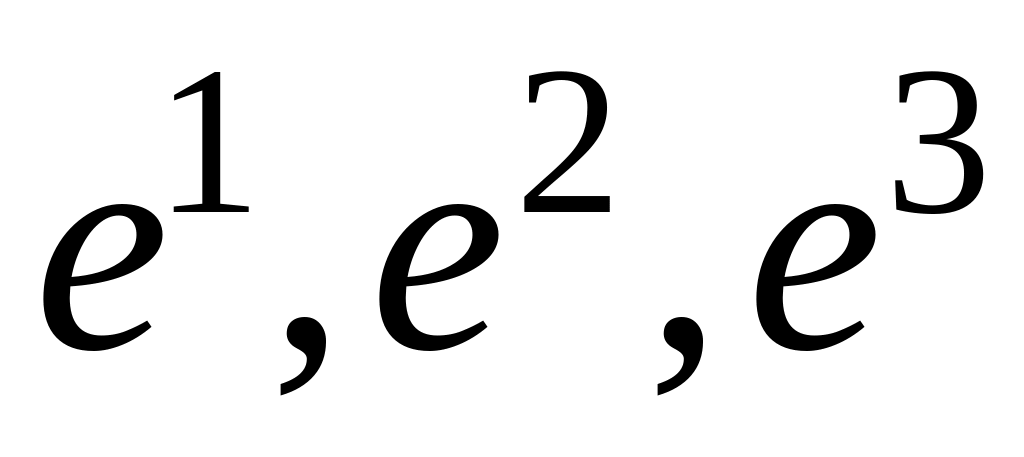. Определить .

9. Дана билинейная форма

Найти ее значение при: а) б)

Задачи

1. Дано

Определить

2. Сколько слагаемых в сумме если ?

3. Упростить

4. Показать что

5. Чему равно если ?

6. Определить где .

7. Проверить линейность отображения , – постоянный вектор.

8. В каком случае функция , является полилинейной формой?

9. Образует ли функция , где – первые координаты векторов 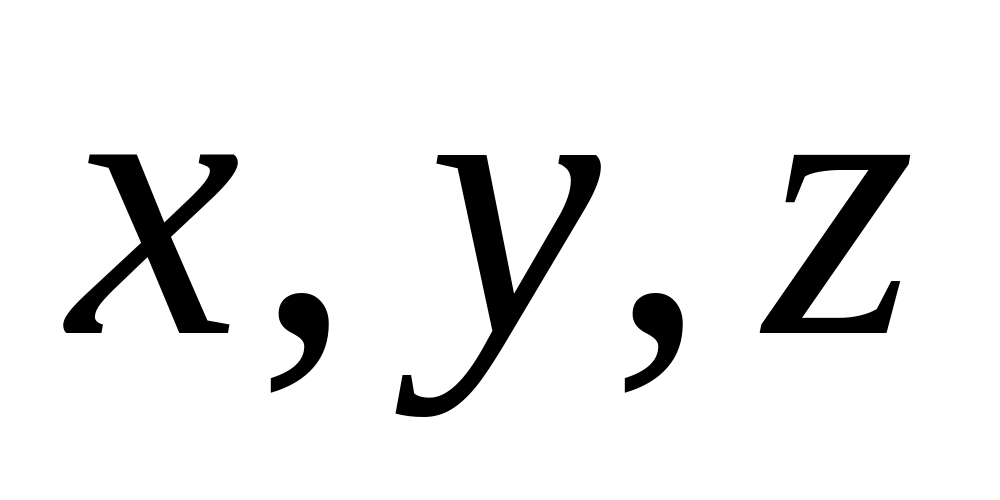полилинейную форму?

10. Доказать что – линейная форма.

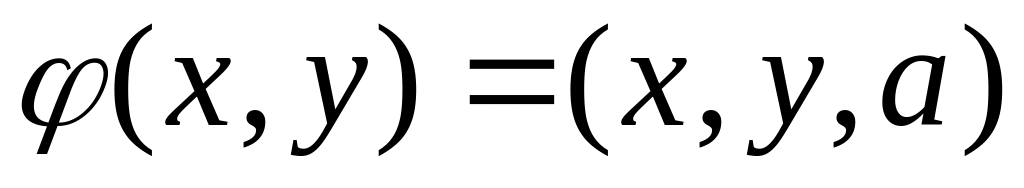11. Доказать, что – билинейная форма.

12. Доказать, что скалярное произведение – билинейная форма.

13. Доказать, что смешанное произведение – трилинейная форма.

14. Придумать примеры линейной, билинейной, трилинейной формы.

Определение тензора

Определение 1. Тензором типа на , -раз контравариантным, и – раз ковариантным называется полилинейное отображение прямого произведения ( берется раз, – раз) в .

Теорема 1. Множество тензоров типа образует векторное пространство размерности , где .

Определение 2. Координатами тензора называются числа где – базис , – базис .

1. Преобразование базиса. – -мерное векторное пространство, – базис, – новый базис.

Формулы перехода от базиса к :

Обратный переход

Матрицы взаимообратные, т.е. ,

где – символ Кронекера.

Теорема 2. При изменении базиса координаты тензора преобразуются по закону

,

где

Имеет место разложение по базису:

,

где – базис

Примеры:

1. Определить координаты линейной формы

, , , , , .

2. Доказать, что где функция на , образует тензор валентности .

Решение:

, , , .

2. Сумма тензоров тогда определится так:

где

Полагая , получим в координатах

.

3. Произведение тензора на скаляр

где , .

4. Тензорное произведение. , тогда и определяется формулой

В координатах

Пример. Определить , где .

, , , , .

Ответ: .

Свойства тензорного произведения:

1)

2)

3)

4)

В общем случае . Привести пример.

Тензорное произведение образует базис .

5. Свертка тензоров – это получение из тензора следующим образом.

Пусть

Свертка произошла по индексам и . В координатах:

Примеры:

1) .

2) .

6. Симметрирование. – подстановка, – знак подстановки.

Определение 3. Тензор получен из путем подстановки .

Определение 4. Тензор называется симметричным, если , антисимметричным, если , .

Теорема 3. симметричен (антисимметричен) , если , .

Определение 5. Симметрированием тензора называется операция

Определение 6. Альтернированием тензора называется операция .

Теорема. – симметричный, – антисимметричный тензоры.

Замечание 1. Симметрировать, альтернировать можно тензоры .

Замечание 2. Симметрирование (альтернирование) можно производить не по всем индексам. Участвующие в симметрировании (альтернировании) индексы берутся в круглые (квадратные) скобки.

Примеры:

1.

2. .

,

.

3. .

4. .

5. .

6. Дискриминантный тензор равен +1, если подстановка – четная, –1, если – нечетная и равен 0, если, по крайней мере, два индекса одинаковы.