Вариант 7

1. Найдите .

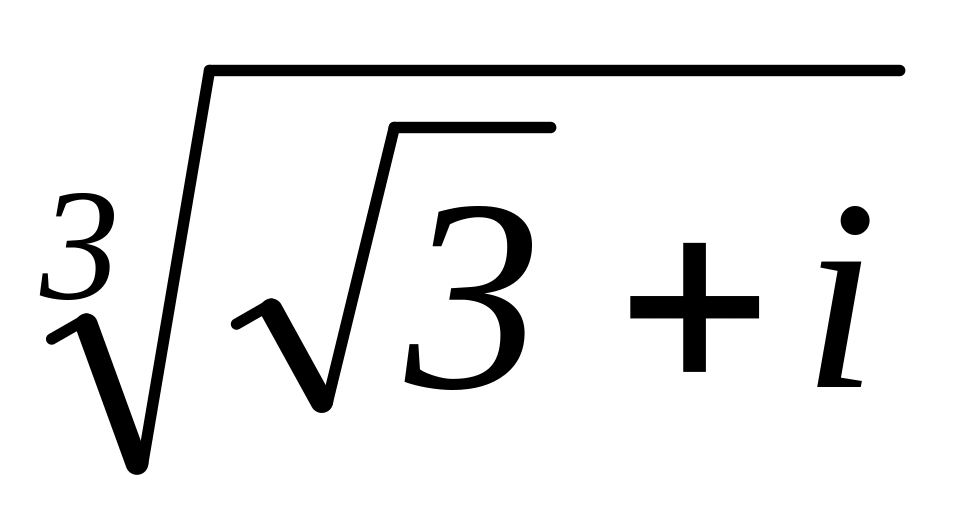2. Решите методом Гаусса .

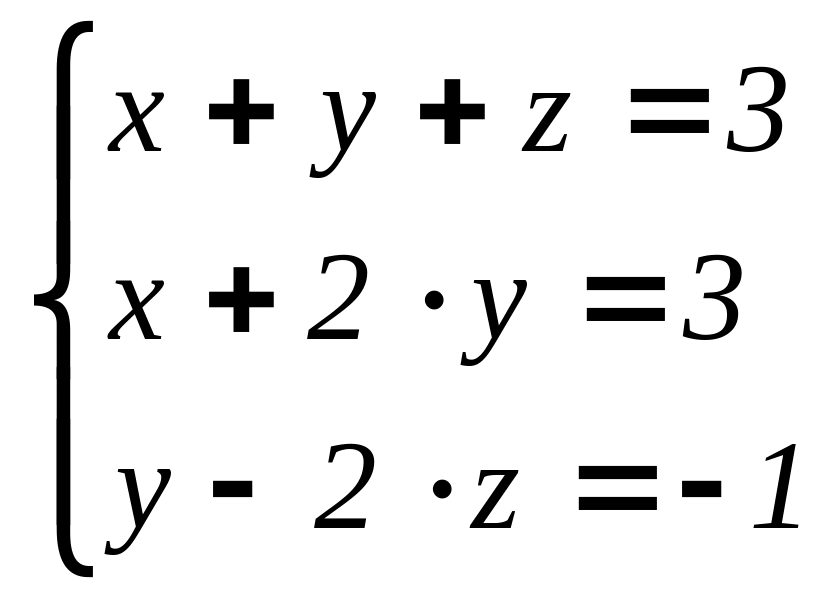3. Двумя способами решите матричное уравнение 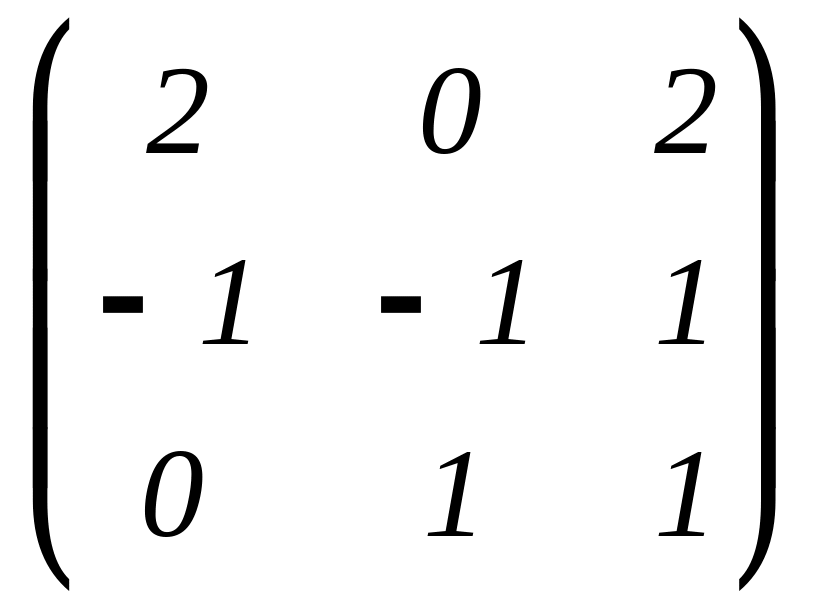X = .

4. Для параллелепипеда ABCDA₁B₁C₁D₁ с вершинами A(0; 0; 1), B(1; 0; 0), C(0; 1; 0), B₁(2; 2; 2) найдите: а) его объём V, б) пло­щадь S_ABCD грани ABCD, в) кано­ническое уравнение прямой l = (B₁A₁), г) угол ((ABB₁), (ABD)) между гранями (ABB₁) и (ABD).

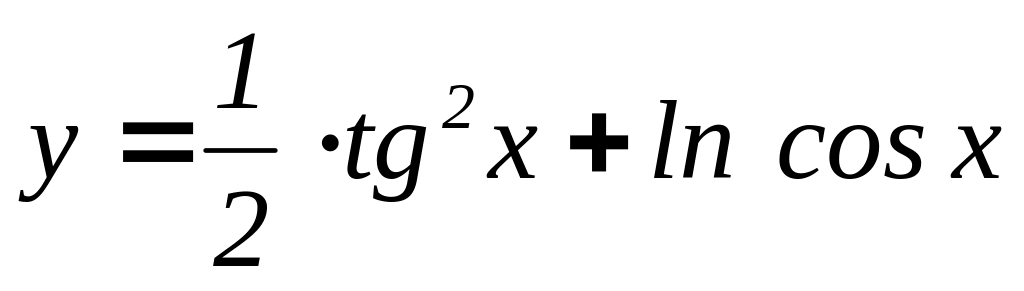5. Найдите производную y(x): а) , б) , в) 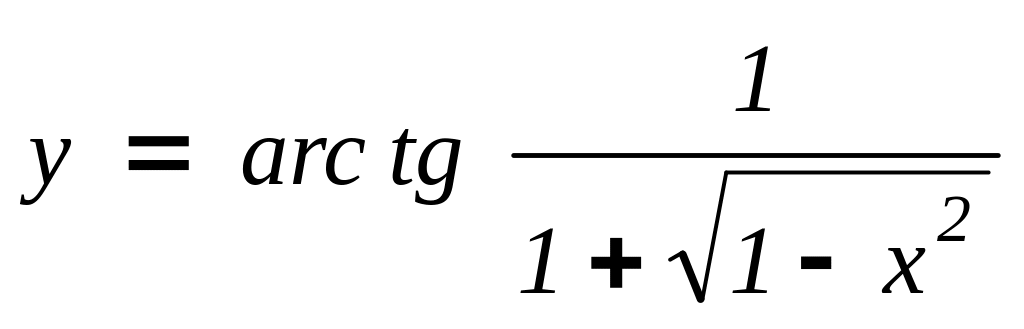, г) x + y³ – 3xy = 0.

6. Исследуйте функцию и постройте график: .

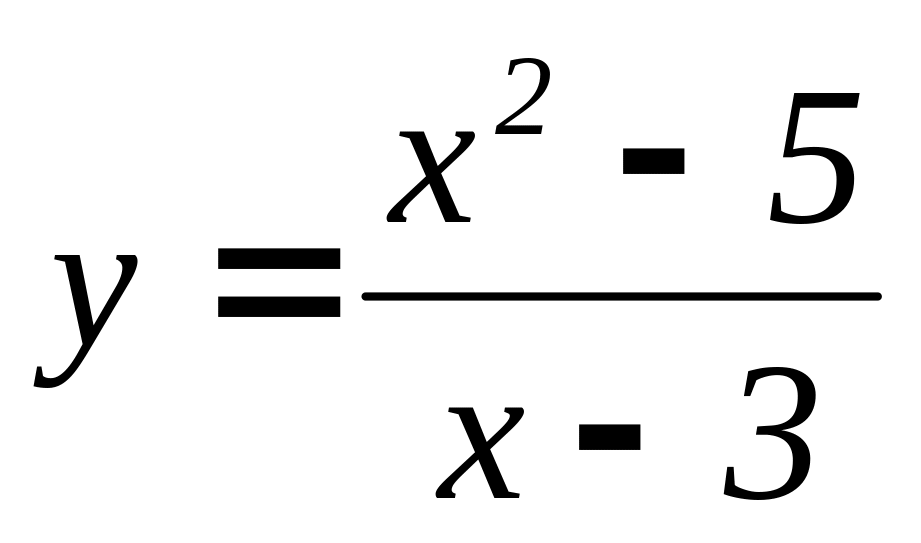Вариант 8

1. Найдите .

2. Решите методом Гаусса .

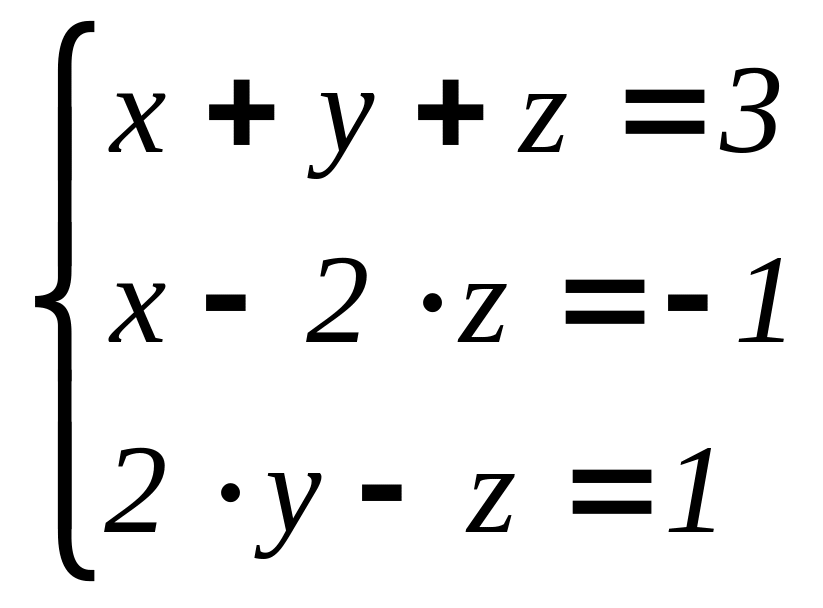3. Двумя способами решите матричное уравнение 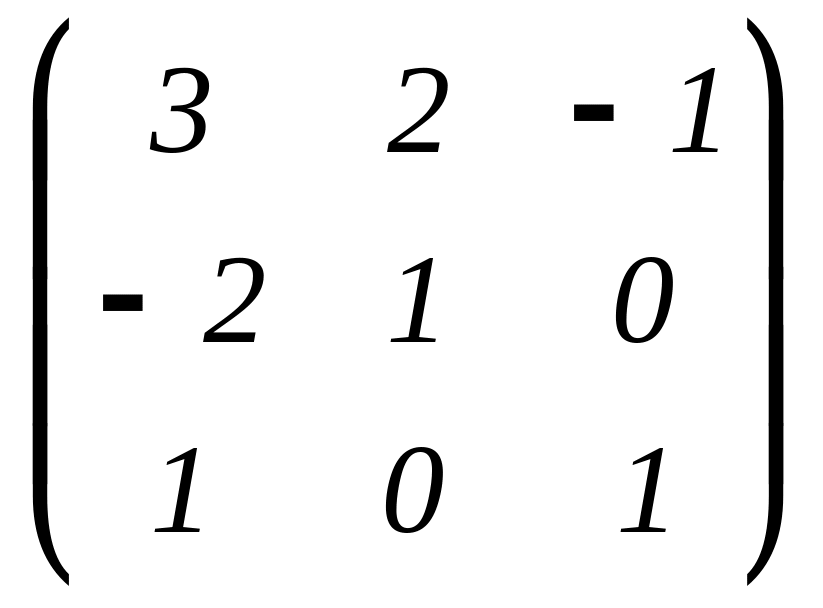X = .

4. Для параллелепипеда ABCDA₁B₁C₁D₁ с вершинами A(0; 0; –1), B(1; 0; 0), C(0; –1; 0), B₁(–1; 1; –1) найдите: а) его объём V, б) пло­щадь S_ABCD грани ABCD, в) кано­ническое уравнение прямой l = (B₁A₁), г) угол ((ABB₁), (ABD)) между гранями (ABB₁) и (ABD).

5. Найдите производную y(x): а) 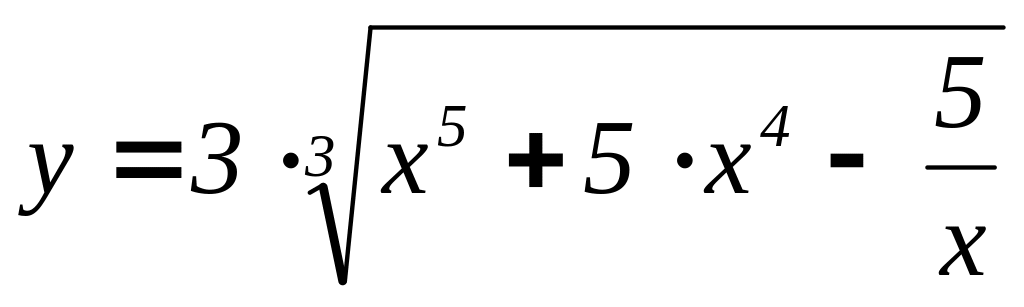, б) 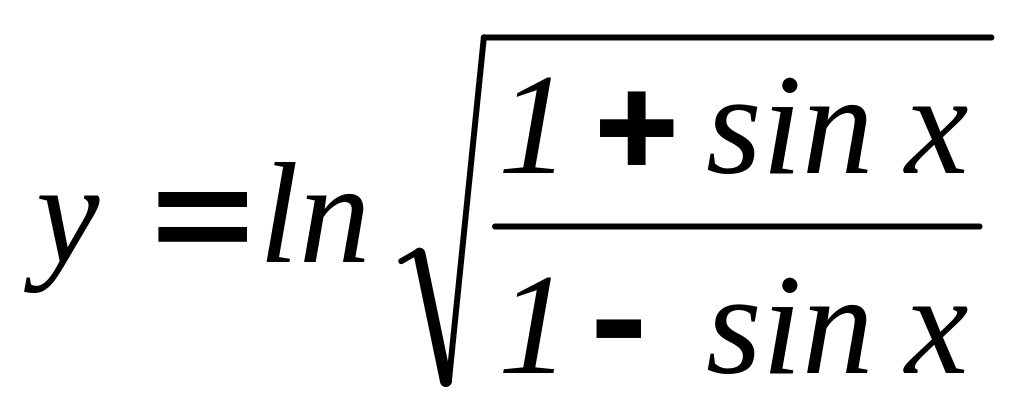, в) y = arc tg(tg² x), г) .

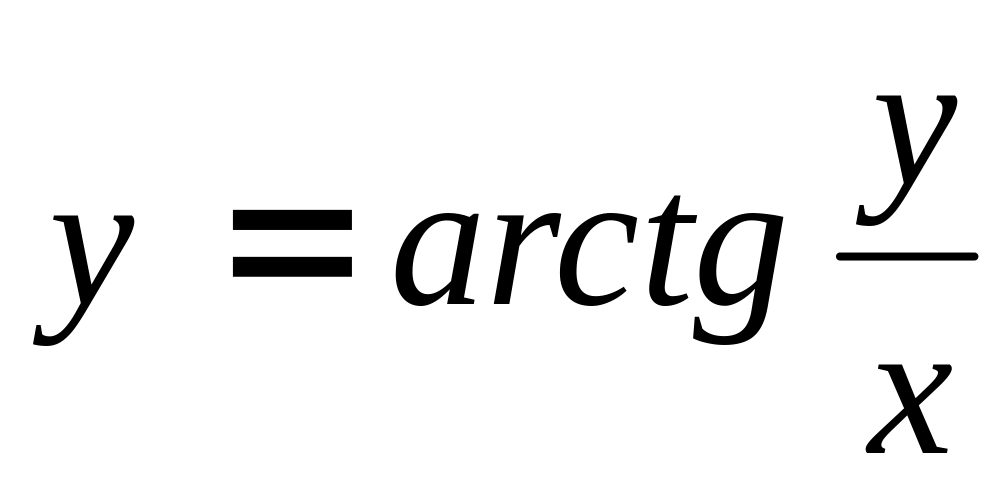6. Исследуйте функцию и постройте график: .

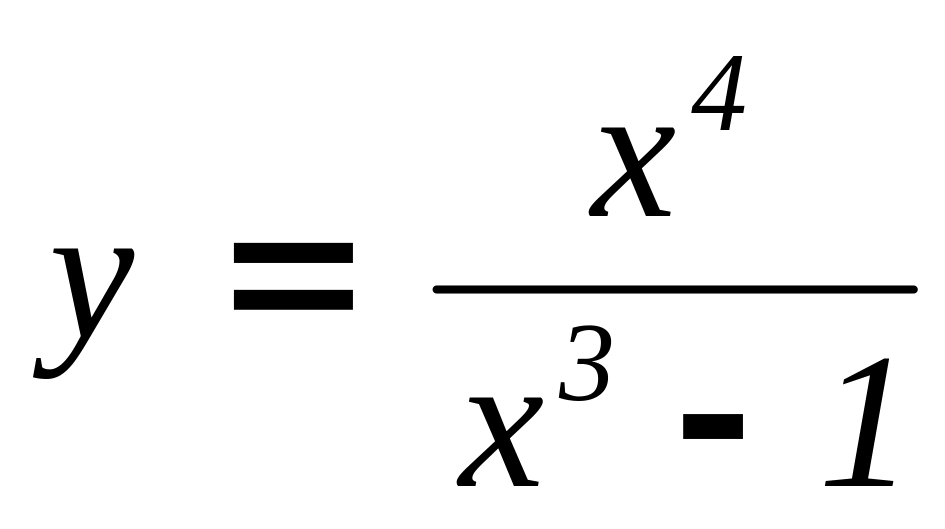Вариант 9

1. Найдите .

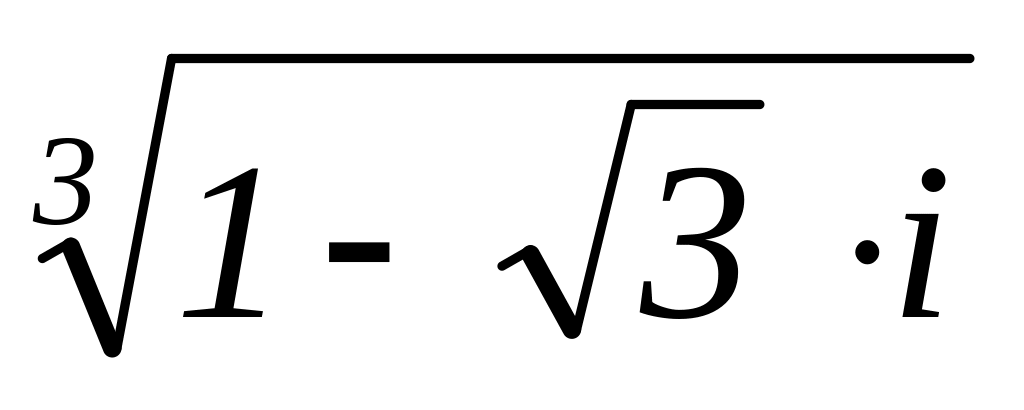2. Решите методом Гаусса .

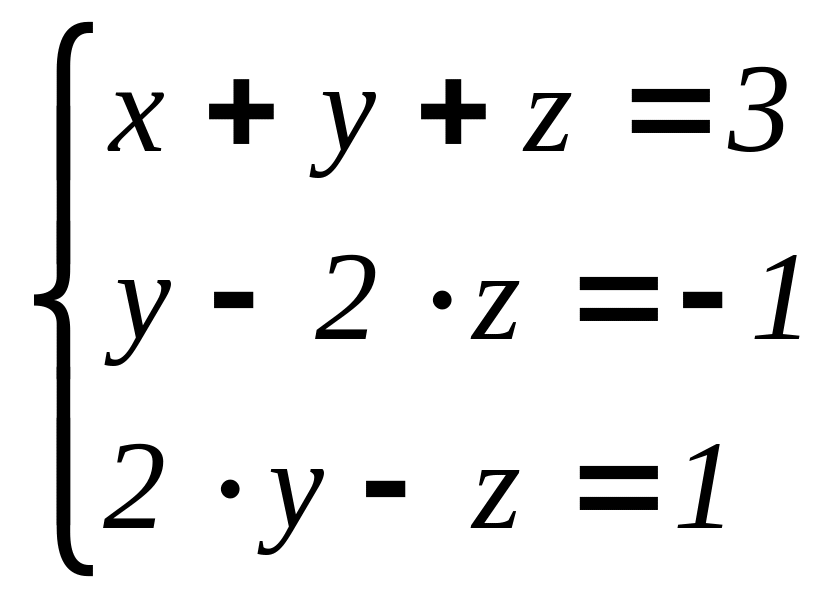3. Двумя способами решите матричное уравнение 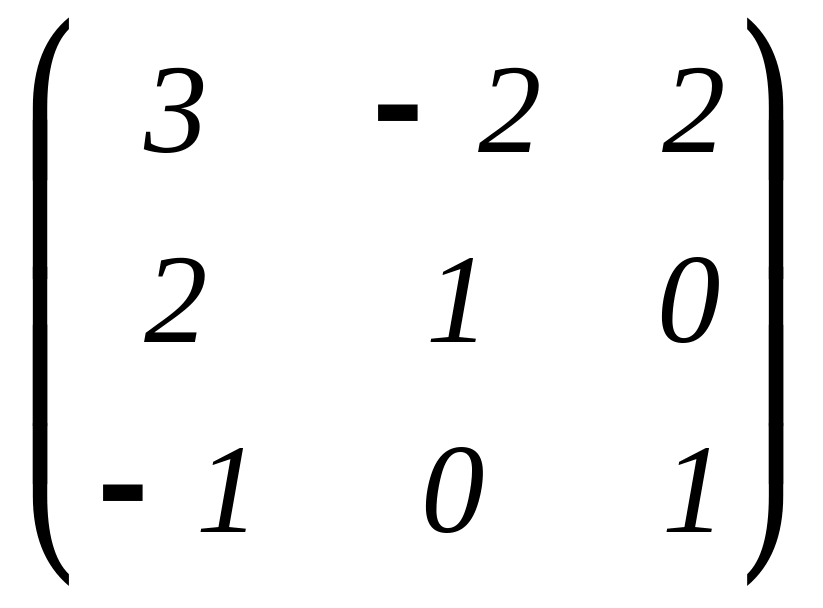X = .

4. Для параллелепипеда ABCDA₁B₁C₁D₁ с вершинами A(–1; 0; 0), B(0; –1; 0), C(0; 0; –1), B₁(–3; –3; –3) найдите: а) его объём V, б) пло­щадь S_ABCD грани ABCD, в) кано­ническое уравнение прямой l = (B₁A₁), г) угол ((ABB₁), (ABD)) между гранями (ABB₁) и (ABD).

5. Найдите производную y(x): а) 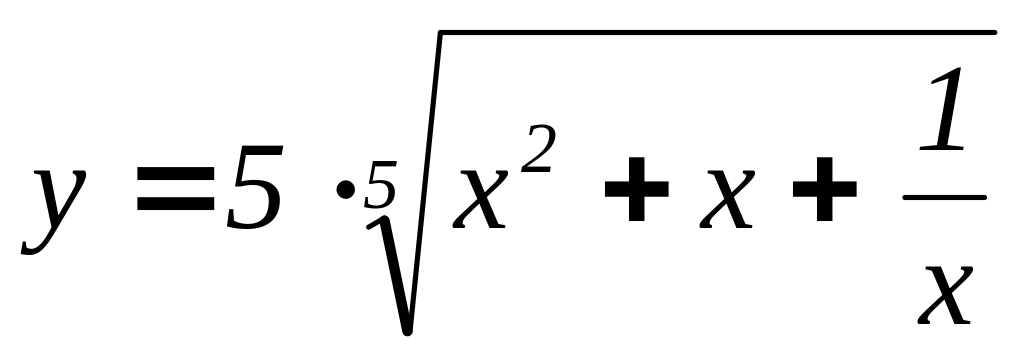, б) y = 2^xe^x , в) 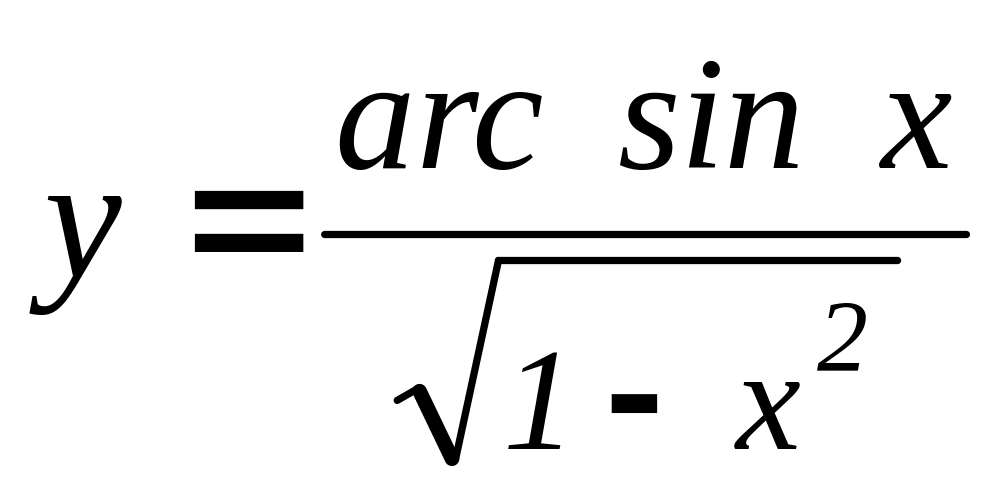, г) xy – y³ + sin y = 0 .

6. Исследуйте функцию и постройте график: .
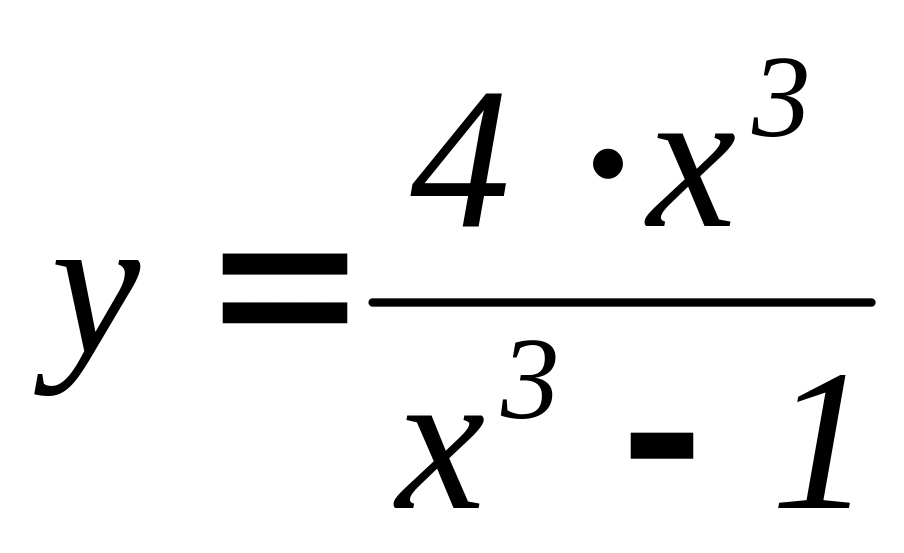