5. Принцип динамической устойчивости

На уровне описания подчиненности функций системы свойство целостности должно быть выражено реализацией такой структуры системы, которая обеспечивает возможность сохранения состава выполняемых функций в их динамическом двойственном взаимном противонаправленном действии между собой и при внешних возмущениях системы. Учитывая, что [Горский Ю.М. Информационная трактовка закона единства и борьбы противоположностей \\ Экпресс-информация. – Иркутск: Из-во Иркутской государственной экономической академии, 1996. – 40с.] фундаментальным основанием в современной науке понятия о динамической устойчивости системы является идея гомеостаза, становится возможным применить её для понимания свойства целостности в аспекте согласованного управляемого противоречия функций системы.

Гомеостат – структура управления материальными объектами, содержащая прямые, обратные и перекрестные связи, обеспечивающая в процессе своей работы поддержание гомеостаза посредством управления внутренним противоречием системы.

Рисунок3. Концептуальная модель гомеостатической системы.

Гомеостаты могут соединяться между собой, вновь образуя самоподобную, гомеостатическую структуру. Однако структура сложных систем не может полностью состоять из гомеостатов. Степень организации системы, с точки зрения проявления свойства целостности системы, на всех уровнях ее организации может быть различной. Динамически устойчивым должно быть ядро системы, а выполнение специфических функций, вынесенных на периферию, не обязательно должно отвечать требованиям динамической устойчивости, что объясняет феномен старения любой системы.

Исходя из вышеописанного следует, что свойство целостности образуется и существует в системе за счет того, что своей структуре система имеет такие информационно-управленческие образования – структурные связи, которые обеспечивают существование системы, как в статическом, так и в динамическом состояниях за счет управления внутренним противоречием системы. Т.е. целостность системы обеспечивается гомеостатическими связями. Гомеостатические отношения необходимы для обеспечения поддержания равновесия в системе в динамике, при взаимодействии функциональных элементов как внутри системы, так при их взаимодействии с внешней средой.

6. Принцип ритмичности.

Всякий естественный процесс существует как ритм, т. к. он поддерживается естественным ритмом причин.

Каждый процесс можно сопоставить с другим процессом, в котором отражается уместность или неуместность с точки зрения гармонии.

В каждом техническом процессе присутствуют ритмы.

Всякие естественные изменения периодичны.

Естественное изменение связано причинной связью.

Периодичность обуславливается ритмом, т. е. усиление или ослабление внутренних факторов.

Следовательно, ритмичность – свойство изменчивости.

Рисунок 8. Функциональная взаимосвязь ритмов.

Рисунок 9. Иерархическая связь ритмов.

Со времен глубокой древности подмечено наличие ритмов и уместность их возникновения:

… Время рождаться и время умирать

Время насаждать и вырывать насажденное

Время убивать и время врачевать

Время разрушать и время строить…

Екклезиаст

Принцип изменчивости

Дж. Миль – закон множественности причин и смешанных следствий.

Причин всегда несколько и несколько способов воздействий, а суммарный эффект не похож ни на одну из причин.

Всегда существует главная причина изменчивости, которая доминирует над другими.

Преобладание выражается в наибольшей тенденции причин изменений.

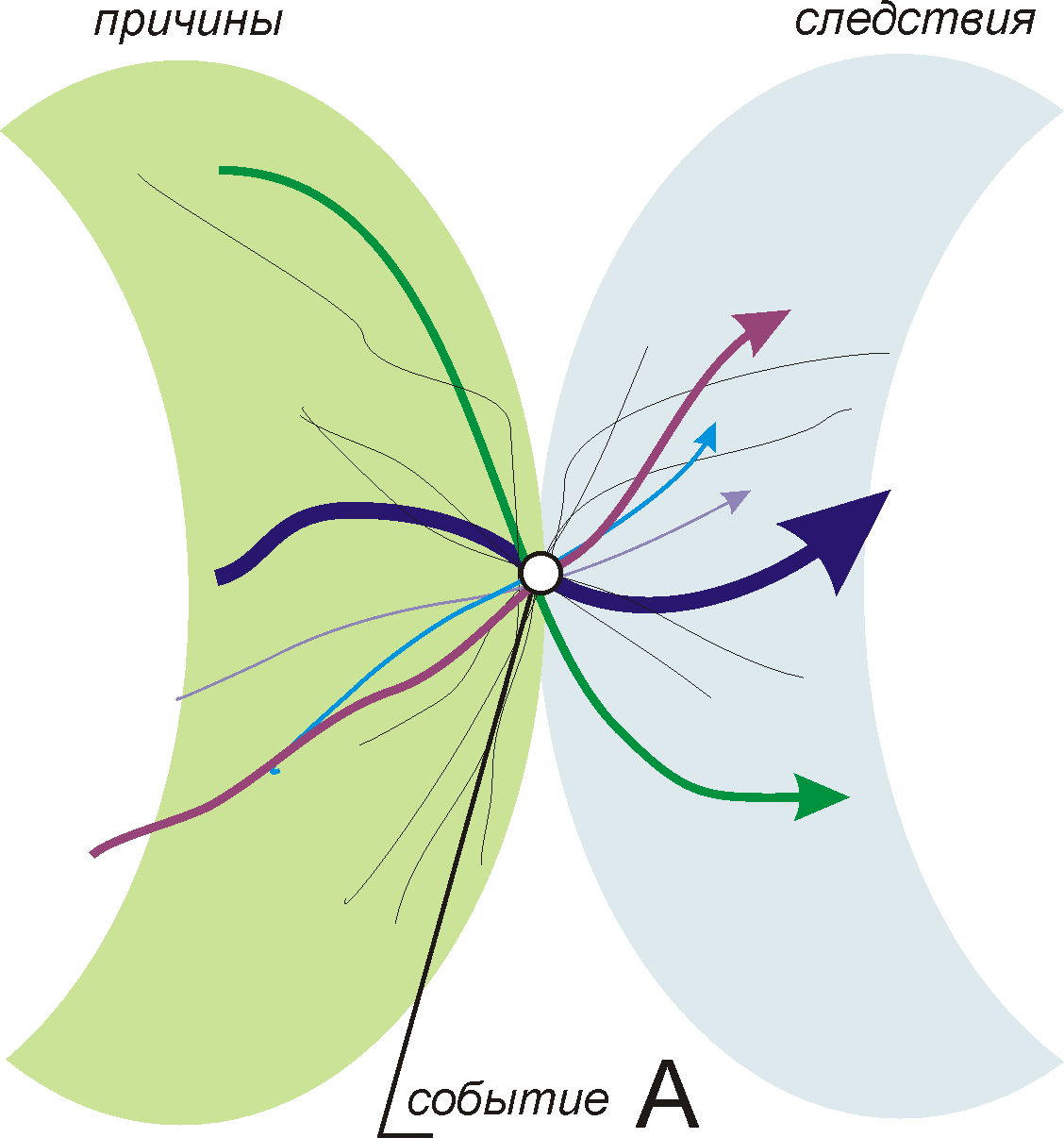
Закон линейной изменчивости – последняя смена состояний некоторого естественного процесса, когда одно состояние сменяет другое последовательно.

Если наблюдаемый процесс происходит под действием одной причины, то можно проследить одну линию изменчивости его состояний, если наблюдаемый процесс происходит под действием нескольких причин, то в нем можно выделить несколько линий изменчивости.

От каждой причины имеется своя естественная линия изменчивости. Тогда каждое состояние исследуемого процесса может быть описано уже через некоторую структуру этой группы линий – структурная изменчивость.

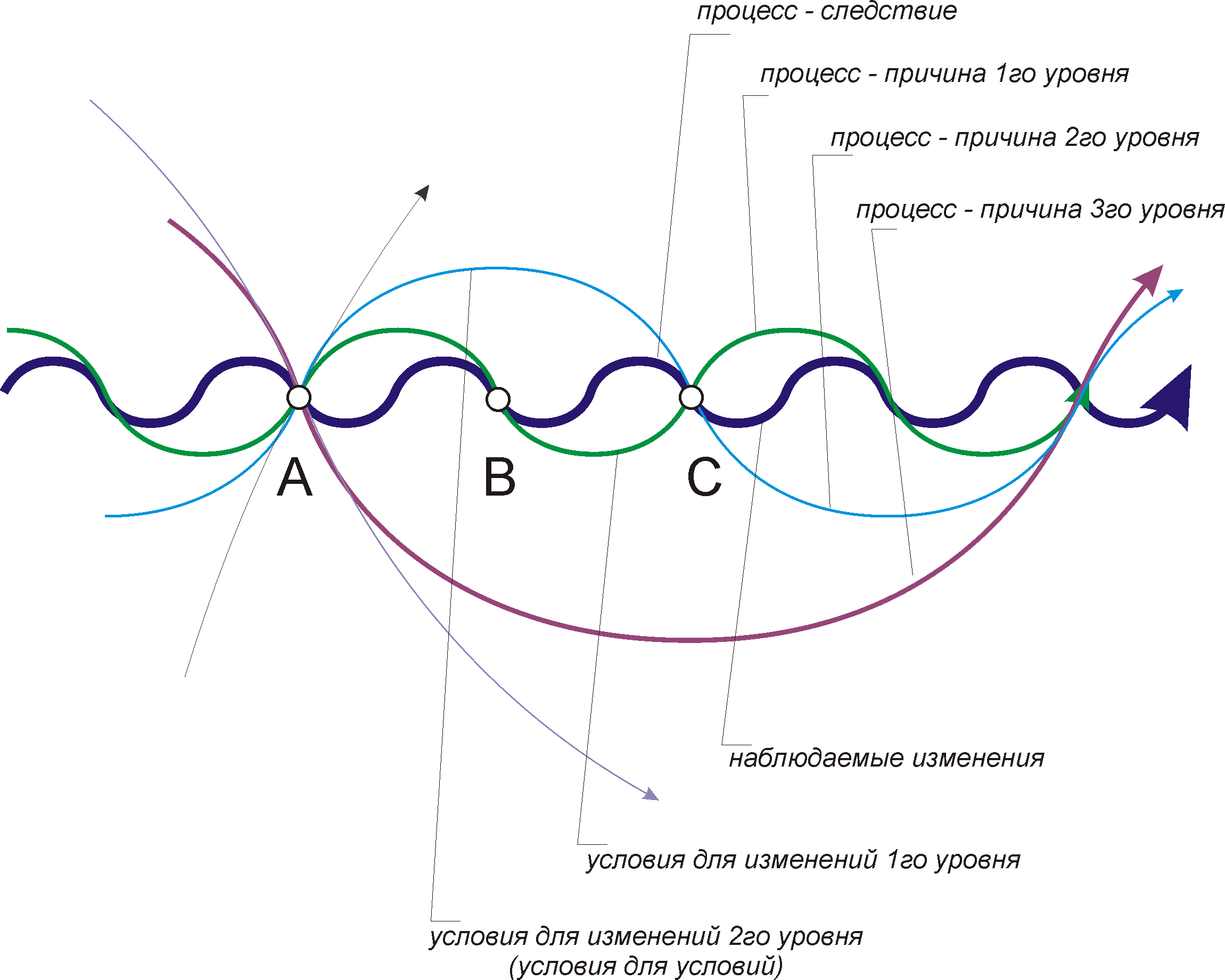
Рисунок 2.2.3. Картина перемен в виде сети причин и условий изменений

Принцип зеркальной изменчивости

Зеркальная изменчивость – обязательное свойство каждого естественного процесса и проявляется как ряд этапов развития некоторого процесса на пути к какому-то пределу возможных состояний, а затем, после достижения этого предела, процесс развивается по тем же этапам в обратном порядке, пока не вернется в исходное состояние.

Следствие изменения изменчивости:

1) Момент зеркального отражения состояния процесса называется инверсией.

Таких инверсий в процессе может быть несколько.

Если в ходе процесса две инверсии превращаются, можно говорить о возвращении к исходному состоянию процесса.

2) Всякую инверсию очередности можно рассматривать как отрицание очередности.

3) Существование инверсии состояний – верный признак зеркальной системы.

4) Диалектическое ориентированное мышление должно знать о естественной суммарности зеркального типа, что является предметом анализа каждого естественного процессов.

Принцип инверсий изменчивости – изменчивость другого рода, когда в ходе естественной эволюции изменяется не только очередность состояний некоторого наблюдаемого процесса, но и сами состояния.

В этом случае мы наблюдаем полную инверсию.

Инверсная изменчивость приводит к состоянию прямо противоположному исходному.

Инверсия изменчивости – обязательное свойство каждого естественного процесса.

Особенности:

1) Изменение естественного процесса имеет существенное отличие по своим правилам, каждые такие изменения которого могут быть незамечены исследователем, а на самом деле они производят существенные изменения.

2) Произошедшие два раза подряд события по принципу инверсной изменчивости возвращают исследователя в то состояние, из которого они наблюдались.

Инверсное

Превращение

Закономерности структурной изменчивости

Принцип структурной изменчивости

Система – множество элементов, выделенных с некоторой точки зрения в объекте, находящиеся в некоторой точке зрения друг с другом, образует целостность.

Структура – совокупность устойчивых связей между элементами, сохраняющаяся при внешней и внутренней изменчивости.

Следствия:

- устойчивая структура каждой естественной целостности определяет ее основные свойства. Изменение структуры приводит к изменению свойств.

- изменение структуры на каждом уровне изменчивости приводит к изменению свойств всей целостности.

структурная изменчивость включает в себя:

- зеркальная изменчивость

- инверсная изменчивость

- образование ритмов на каждом уровне иерархии системы

- образование цикличности процессов в системе

Таким образом, чтобы понять явления, нужно понять структуру и исключительные проявления структуры.

Для прогноза изменений необходимо умение включать во внимание те или иные факторы причины развития естественных процессов и их ритмы перемен на тех или иных уровнях структуры.

Лекция 4

О всеобщем законе гармонии. Золотая пропорция. Числа Фибоначчи.

Закон чисел Фибоначчи (1180 – 1240)

Основа закона гармонии мира

Задача последовательности Фибоначчи

Некто поместил пару кроликов в некотором месте, чтобы узнать сколько кроликов родится в течение года, если природа кроликов такова, что через месяц пара кроликов производит на свет другую пару, а рождают кролики со второго месяца после своего рождения.

Следующий месяц: 1+1=2

4: 2+1=3

5: 3+2=5

6: 5+3=8

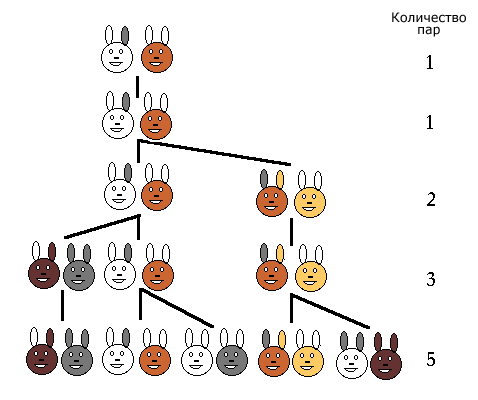
F_n=F_n-1+F_n-2

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233

Следующее число – сложение двух предыдущих.

Эта последовательность в своем отношении между числами ассимптотична приближению к некоторому постоянному соотношению.

Если какой-либо член последовательности F разделить на предшествующий ему, величина будет иррациональная - примерно равна 1,618.

Современник, друг да Винчи, лука Паччоли (книга «Золотое сечение») назвал - «божественной пропорцией».

Да Винчи нашел эти соотношения в строении тела человека, животных, растений и использовал при написании картин.

Фибоначчи в свое время опубликовал три большие работы, самая знаменитая из которых называется "Liber Abaci". Благодаря этой книге Европа узнала индо-арабскую систему чисел, которая позднее вытеснила традиционные для того времени римские числа. Работы Фибоначчи имели огромное значение для последующего развития математики, физики, астрономии и техники. В "Liber Abaci" Фибоначчи приводит свою последовательность чисел как решение математической задачи - нахождение формулы размножения кроликов. Числовая последовательность такова: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 (далее до бесконечности). Последовательность Фибоначчи имеет весьма любопытные особенности, не последняя из которых - почти постоянная взаимосвязь между числами.

• Сумма любых двух соседних чисел равна следующему числу в последовательности. Например: 3 + 5 = 8; 5 + 8 = 13 и т.д.

• Отношение любого числа последовательности к следующему приближается к 0,618 (после первых четырех чисел). Например: 1: 1 = 1; 1: 2 = 0,5; 2: 3 = 0,67; 3: 5 = 0,6; 5: 8 = 0,625; 8: 13 = 0,615; 13: 21 = 0,619 и т.д. Обратите внимание, как значение соотношений колеблется вокруг величины 0,618, причем размах флуктуаций постепенно сужается; а также на величины: 1,00; 0,5; 0,67.

• Отношение любого числа к предыдущему приблизительно равно 1,618 (величина обратная 0,618). Например: 13: 8 = 1,625; 21: 13 = 1,615; 34: 21 = 1,619. Чем выше числа, тем более они приближаются к величине 0,618 и 1,618.

• Отношение любого числа к следующему за ним через одно приближается к 0,382, а к предшествующему через одно - 2,618. Например: 13: 34 = 0,382; 34: 13 = 2,615.

Последовательность Фибоначчи содержит и другие любопытные соотношения, или коэффициент, но те, которые мы только что привели - самые важные и известные. Как мы уже подчеркивали выше, на самом деле Фибоначчи не является первооткрывателем своей последовательности. Дело в том, что коэффициент 1,618 или 0,618 был известен еще древнегреческим и древнеегипетским математикам, которые называли его "золотым коэффициентом" или "золотым сечением". Его следы мы находим в музыке, изобразительном искусстве, архитектуре и биологии. Греки использовали принцип "золотого сечения" при строительстве Парфенона, египтяне - Великой пирамиды в Гизе. Свойства "золотого коэффициента" были хорошо известны Пифагору, Платону и Леонардо да Винчи.

Золотое сечение

Человек разделяет окружающие его предметы по форме.

Целое состоит из частей или соотношения этих вещей.

Золотое сечение – такое пропорциональное деление отрезка на неравные части, при котором целый так соотносится к большему отрезку, как больший к меньшему.

Отношение отрезков золотого сечения выражается иррациональной дробью 0,618

Пифагор: «В основе всего находится число»

Аристотель: «Число – сущность всех вещей и организация Вселенной в ее определении представляет гармонию системы чисел»

Золотой треугольник

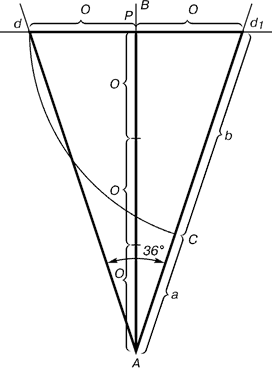
Существует золотой кубоид - прямоугольный параллелепипед с ребрами, имеющими длины 1.618, 1 и 0.618.

Пифагор построил правильный пятиугольник.