Задание 15. Статистическое регулирование технологического процесса
Цель работы - овладеть практическими навыками по применению методов статистического регулирования технологических процессов по количественному признаку.
Краткие теоретические сведения
Статистические методы управления качеством, являясь эффективным средством повышения качества промышленной продукции, широко применяются в серийном и массовом производстве. Они основаны на методах математической статистики и позволяют по ограниченному числу наблюдений принимать решения при управлении качеством продукции. Статистические методы предупреждают появление брака путем статистического наблюдения за состоянием оборудования. Управление качеством продукции в процессе изготовления осуществляется методами приемочного контроля и статистического регулирования. Метод статистического регулирования технологического процесса обеспечивает нормальный отлаженный ход технологического процесса, что гарантирует требуемое качество продукции и исключает брак.
В настоящее время для различных производственных условий разработан ряд методов статистического регулирования: метод средних арифметических значений и размахов; метод средних значений и метод средних квадратических отклонений; метод медиан и индивидуальных значений. Рассмотрим один из них.
Метод средних арифметических значений и размахов применяется при дву- и односторонних погрешностях, подчиняющихся соответственно закону нормального распределения Гаусса либо Максвелла. При этом методе пользуются двумя основными статистическими характеристиками: средним арифметическим значением
где
–
–
замер контролируемого параметра;
n – количество замеров в выборке, и размахом варьирования данной выборки
где
–
наибольшее и наименьшее значения в
выборке.
Средние значения X содержат информацию об уровне настроенности процесса,
размахи R - сведения о рассеянии показателя качества, т.е. о точности процесса.
Об уровне стабильности технологического процесса судят по данным контрольной карты (рис.15.1.), которая предназначена для графической иллюстрации изменения уровня
настройки и точности процесса. Контрольная карта (метод X-R) состоит из двух диаграмм: диаграммы средних арифметических значений и диаграммы размахов.
На диаграмму средних арифметических значений наносят: сплошные горизонтальные
линии
пределов допуска (верхнего -
и
нижнего
);
штриховые линии, ограничивающие
зону
допускаемых отклонений средних значений
выборок (верхнего
и нижняя Рн)
.
На диаграмму размахов, расположенную в нижней части карты, наносят также контрольные и предупредительные границы: нижнюю сплошную линию, соответствующую, как правило, нулевой отметке; штриховую линию PBR, соответствующую верхней границе регулирования размахов; сплошную линию TBR - верхний предел допуска.
Если средние арифметические значения выборок не выходят за предупредительные
границы и Рн, а размахи - за верхнюю границу регулирования PBR, то технологический процесс протекает удовлетворительно. В случае нарушения данного условия, т.е. отклонения от нормального хода процесса, необходимо взять внеочередную выборку. Если выход точек за границы регулирования повторится, то необходимо остановить работу и устранить причину, вызвавшую сбой хода технологического процесса. На карте при этом отмечается разладка процесса в виде стрелки. Партия продукции, выпущенная между двумя последовательными выборками, должна быть проверена методом сплошного контроля.
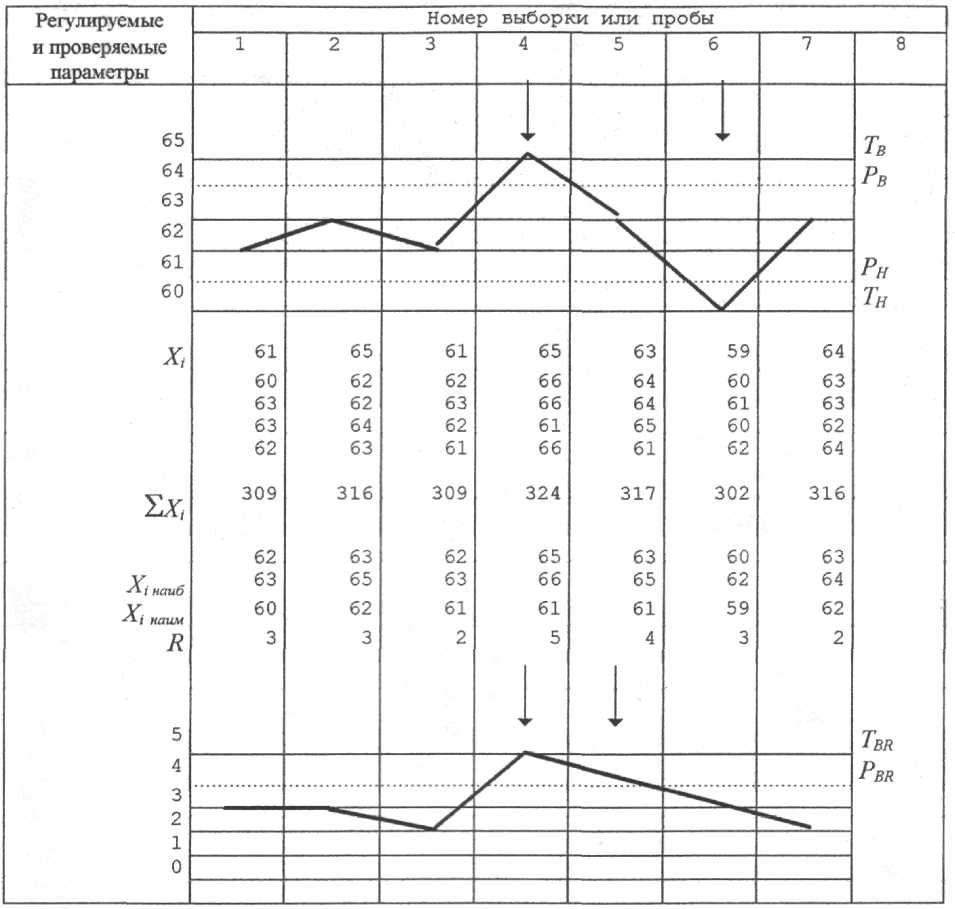
Рис.15.1. Контрольная карта средних арифметических значений и размахов
измеряемого параметра.
Содержание и порядок выполнения работы
В качестве исходной информации студенты получают заполненный протокол результатов измерений контролируемого параметра (размера, массы, температуры и т.п.), значение поля допуска, закон распределения измеренного образца. Замеры, предоставляемые в протоколе, произведены в соответствующих пробах, взятых через равные временные интервалы.
По данным протокола с помощью микрокалькулятора рассчитываются основные статистические характеристики (средние арифметические значения и размахи варьирования), результаты которых указываются на поле между диаграммами контрольной карты.
Далее в соответствии с известным законом распределения рассчитываются границы регулирования (контрольные и предупредительные) для принятых статистических характеристик и наносятся на контрольную карту на соответствующие зоны диаграмм.
По результатам расчета значений статистических характеристик на контрольной карте строятся диаграммы изменения этих характеристик в выборках (пробах).
На заключительном этапе производится анализ контрольной карты и по положению точек на диаграммах делается вывод о состоянии технологического процесса. В случае выявления отклонений от нормального хода технологического процесса (выход отдельных значений характеристик за предупредительные границы)необходимо указать действия контролера и мероприятия для устранения сбоев в технологическом процессе и предупреждение брака.
Между диаграммами производят запись исходных данных и расчетных значений характеристик в выборках (см.рис.15.1.). Объем выборки чаще всего принимают 3-10 единиц. Он зависит от стабильности, производительности и других факторов. Период отбора выборок составляет 1-2 часа.
Границы регулирования рассчитывают в зависимости от объема выборки и значения допуска.
В
стандарте предусмотрены:
– граница регулирования для средних
арифметических значений; 2.5
– граница регулирования для размахов.
Границы регулирования Рв и Рн диаграмм средних арифметических значений выборок для показателей качества, распределяемых по закону Гаусса, находят по формулам:
(3)
(4)
где – половина допуска; Тв и Тн - верхний и нижний пределы допуска;
А – коэффициент, зависящий от объема выборки.
Границу
регулирования для размахов
вычисляют по формуле
(5)
где D - коэффициент, зависящий от объема выборки. Значения коэффициентов А и D приведены ниже.
Выборка |
А |
D |
3 |
0.423 |
1.45 |
4 |
0.500 |
1.56 |
5 |
0.553 |
1.63 |
6 |
0.592 |
1.68 |
7 |
0.622 |
1.72 |
8 |
0.646 |
1.75 |
9 |
0.667 |
1.78 |
10 |
0.684 |
1.81 |
Работа выполняется на основе вариантов исходных данных:
1-й вариант (номинальный размер 50 мм., допуск =±0.3 мм.)
Номер экземпляра в пробе |
Номер пробы |
|||||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
1 |
50.3 |
50.2 |
50.1 |
49.8 |
49.6 |
49.3 |
50.1 |
50.2 |
50.1 |
50.0 |
49.8 |
50.2 |
2 |
50.1 |
50.0 |
50.2 |
49.7 |
50.1 |
5.0 0 |
50.3 |
50.3 |
50.2 |
49.9 |
50.1 |
50.1 |
3 |
50.2 |
50.1 |
49.7 |
50.0 |
49.9 |
50.2 |
50.4 |
50.3 |
50.2 |
49.9 |
50.1 |
50.3 |
2-й
вариант (номинальный размер 50 мм., допуск
мм)
Номер экземпляра в пробе |
Номер пробы |
|||||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
Е ) |
9 |
10 |
11 |
12 |
|
1 |
50.0 |
50.2 |
50.0 |
50.0 |
49.9 |
50.2 |
49.9 |
49.8 |
50.2 |
50. 2 |
50.3 |
50.1 |
2 |
50.1 |
50.4 |
50.0 |
49.7 |
50.1 |
50.1 |
50.2 |
50.0 |
50.1 |
49.9 |
50.2 |
50.0 |
3 |
50.3 |
50.3 |
50.1 |
49.8 |
50.2 |
49.6 |
50.0 |
50.1 |
50.4 |
50.0 |
50.1 |
50.4 |
3-й вариант (номинальный размер 67 мм., допуск = ±0.5 мм.)
Номер экземпляра в пробе |
Номер пробы |
|||||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
1 |
67.3 |
67.2 |
67.0 |
67.2 |
67.4 |
66.8 |
67.2 |
67.2 |
66.8 |
67.2 |
66.9 |
67.2 |
2 |
67. 2 |
67.4 |
67.3 |
66.7 |
66.6 |
66.9 |
67.4 |
66.9 |
67.0 |
66.7 |
67.1 |
67.1 |
3 |
67.2 |
67.5 |
67.2 |
67.3 |
66.7 |
67.2 |
67.3 |
66.8 |
67.1 |
66.8 |
67.3 |
66.8 |
4-й вариант (номинальный размер 56 мм., допуск = ±0.3 мм.)
Номер экземпляра в пробе |
Номер пробы |
|||||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
1 |
56.2 |
56.3 |
56.1 |
56.2 |
56.0 |
55.8 |
56.3 |
56.3 |
55.9 |
56.2 |
55.8 |
55.7 |
2 |
56.1 |
56.1 |
55.8 |
56.4 |
56.1 |
55.7 |
56.2 |
56.4 |
55. 7 |
56.3 |
56.1 |
56.3 |
3 |
56.3 |
55.9 |
55.9 |
56.1 |
55.7 |
56.1 |
56.2 |
56.2 |
56.1 |
55.6 |
55.9 |
56.2 |