Решение типового варианта индивидуального задания №2
1.Ряды
Задача
№1.
Найти сумму
ряда
.
Решение:
Выведем
формулу частичной суммы ряда Sn.
Для этого разложим общий член ряда
на сумму простых дробей. Сначала
представим квадратный трехчлен в виде
произведения простых множителей:
Теперь общий член ряда представим в виде суммы простых дробей с неопределенными коэффициентами
.
Найдем числа А
и В,
сравнив коэффициенты при одинаковых
степенях n
Итак,
Выведем формулу частичной суммы ряда Sn:
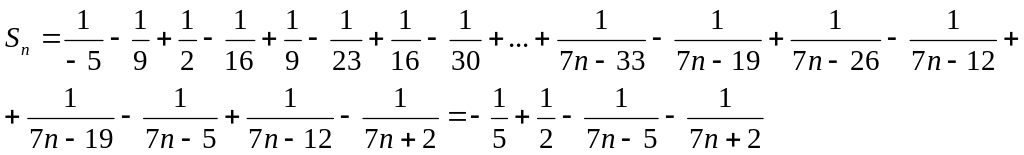
По определению
сумма ряда
Ответ:
.
Задача
№2.
Исследовать
на сходимость ряд
Решение:
Используем
признак Даламбера,
вычисляя
у нас
,
.
Получим
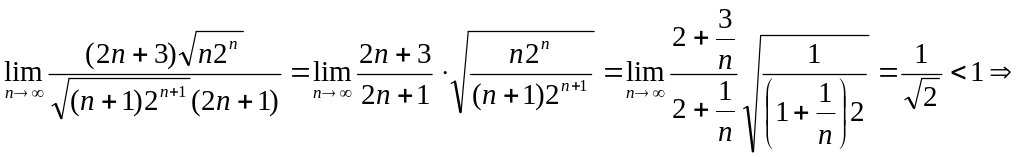
ряд сходится.
Задача
№3.
Исследовать
на сходимость ряд
Решение:
Применим
радикальный признак Коши, вычисляя
у нас:
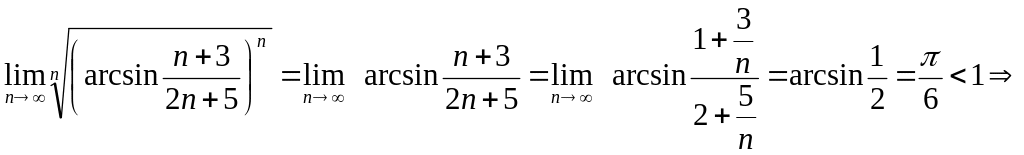ряд сходится.
Задача
№4.
Исследовать
на сходимость ряд
Решение: Применим интегральный признак Коши, исследуя на сходимость несобственный интеграл первого рода:
Следовательно, интеграл расходится, а значит, расходится и данный ряд.
Задача
№5.
Исследовать
на сходимость ряд
Решение: К данному знакочередующемуся ряду применим признак Лейбница.
1) Докажем, что
последовательность
убывающая. Начнем с очевидного неравенства:
если мы умножим правую часть неравенства
на выражение, большее 1, то только его
«усилим», т.е. очевидно, что
.
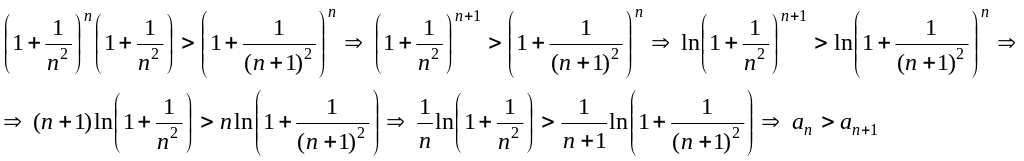Что и
требовалось
доказать.
2) Вычислим
Для этого, используя правило Лопиталя,
найдем предел функции.
Таким образом,
признак
Лейбница выполнен, значит знакочередующийся
ряд сходится. Уточним характер сходимости
ряда. Ряд из абсолютных величин исходного
можно сравнить с расходящимся
гармоническим
рядом
.
ряды ведут
себя
одинаково
т.е. данный ряд
как и
гармонический, расходится, следовательно,
исходный знакочередующийся ряд сходится
условно.
Задача
№6. Найти
область сходимости ряда
Решение: Применим радикальный признак Коши при нахождение области сходимости ряда.
Исследуем ряд на
границе области сходимости, т.е. при
и при
.
При
получим числовой ряд
применим к данному ряду признак
Даламбера, получим:
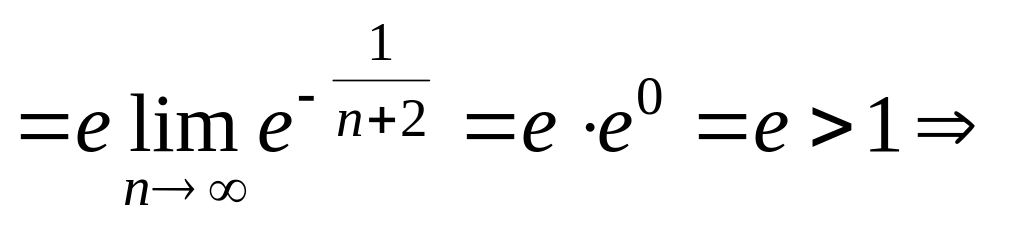ряд
сходится. При
получим ряд
знакочередующийся вида
Применяя
к нему признак Лейбница,
найдем
,
получим:
ряд
сходится.
Ответ:
Область сходимости исходного ряда:
Задача
№7.
Найти
область сходимости ряда
Решение: Применим признак Даламбера
При х =
2
горманический
ряд сходится. (2n-1)
– нечетно при любом n
т.е. (-1)2n-1=
- 1.
Значит х = 2
области сходимости.
При х = 8
- знакочередующийся ряд, по признаку.
Лейбница:
1)
- убывающая последовательность.
2)
.
Итак, ряд
сходится условно, т.к. ряд из абсолютных
величин исходного является гармоническим,
следовательно, расходящимся рядом;
значит, х = 8
области сходимости ряда.
Ответ: 2 < х ≤ 8.
Задача
№8.
Найти интервал сходимости степенного
ряда
.
Решение:
Применим
признак Даламбера
.
Ответ: .
Задача
№9.
Вычислить с помощью рядов интеграл
.
Решение:
Применим
формулу разложения функции в ряд
