
- •Методические указания к выполнению лабораторных работ по электротехническим дисциплинам
- •6.050502 – Инженерная механика,
- •6.050702 – Автомобильный транспорт
- •Часть 4
- •Введение
- •Лабораторная работа №21 исследование одиночного усилительного каскада
- •21.1. Цель работы
- •21.2. Теоретические сведения
- •21.3. Порядок выполнения работы
- •21.4. Содержание отчета
- •21.5. Контрольные вопросы
- •Лабораторная работа №22 Элементная база и принципы работы электронной лаборатории Electronics Workbench
- •22.1. Цель работы
- •22.2. Теоретические сведения
- •22.3. Порядок выполнения работы
- •21.4. Содержание отчета
- •21.5. Контрольные вопросы
- •Лабораторная работа №23 исследование дифференциального усилителя на биполярных транзисторах
- •23.1. Цель работы
- •23.2. Теоретические сведения
- •23.3. Порядок выполнения работы
- •Лабораторная работа №24 исследование арифметических блоков аналоговых вычислительных устройств
- •24.3. Порядок выполнения работы
- •24.4. Содержание отчета
- •24.5. Контрольные вопросы
- •Лабораторная работа №25 исследование дифференцирующих и интегрирующих устройств аналоговых вычислительных машин
- •25.1. Цель работы
- •25.2. Теоретические сведения
- •25.3. Порядок выполнения работы
- •25.4. Содержание отчета
- •25.5. Контрольные вопросы
- •Лабораторная работа №26 исследование базовых логических элементов цифровых вычислительных машин
- •26.1. Цель работы
- •26.2. Теоретические сведения
- •26.3. Порядок выполнения работы
- •26.4. Содержание отчета
- •26.5. Контрольные вопросы
- •Лабораторная работа №27 исследование основных цифровых комбинационных устройств (дешифратора, демультиплексера, мультиплексера)
- •27.1. Цель работы
- •27.2. Теоретические сведения
- •27.3. Порядок выполнения работы
- •27.4. Содержание отчета
- •27.5. Контрольные вопросы
- •Лабораторная работа №28 исследование триггеров, счетчиков импульсов и регистров сдвига
- •28.1. Цель работы
- •28.2. Теоретические сведения
- •28.3. Порядок выполнения работы
- •28.4. Содержание отчета
- •28.5. Контрольные вопросы
- •Лабораторная работа №29 исследование аналого-цифровых и цифро-аналоговых преобразователей
- •29.1. Цель работы
- •29.2. Теоретические сведения
- •29.3. Порядок выполнения работы
- •29.4. Содержание отчета
- •29.5. Контрольные вопросы
- •Лабораторная работа №30 исследование четырехразрядного параллельного сумматора
- •30.1. Цель работы
- •30.2. Теоретические сведения
- •30.3. Порядок выполнения работы
- •30.4. Содержание отчета
- •30.5. Контрольные вопросы
- •Лабораторная работа №31 изучение учебно-отладочного устройства
- •31.1. Цель работы.
- •31.2. Самостоятельная работа
- •31. 3. Содержание и порядок выполнения лабораторной работы
- •31.4. Содержание отчета
- •31.5. Контрольные вопросы
- •Лабораторная работа №32 изучение арифметических команд и команд пересылки данных
- •32.1. Цель работы.
- •32.2. Самостоятельная работа
- •32.3. Содержание лабораторной работы
- •32.4. Порядок выполнения работы
- •32.5. Содержание отчета
- •32.6. Контрольные вопросы
- •Лабораторная работа №33 обработка массивов информации. Организация циклов
- •33.1. Цель работы.
- •33.2. Самостоятельная работа
- •33.3. Содержание лабораторной работы
- •33.4. Порядок выполнения работы
- •33.5. Содержание отчета
- •33.6. Контрольные вопросы
- •Библиографический список
- •Приложение в Варианты заданий к лабораторной работе 33
29.5. Контрольные вопросы
1. Сформулируйте правило перевода десятичного числа в двоичную систему счисления.
2. Сформулируйте правило перевода двоичного числа в десятичную систему счисления.
3. Сформулируйте правило перевода двочного числа в шестнадцатиричную систему счисления.
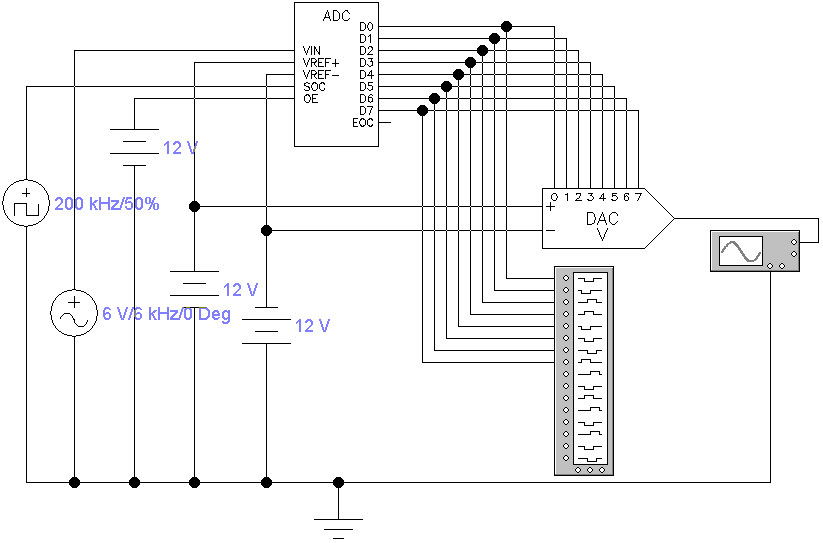
Рисунок 29.10 – Схема экспериментальной установки для изучения работы цифро-аналогового преобразователя
4. Поясните назначение и условное обозначение цифро-аналогового преобразователя, назначение выводов ЦАП.
5. Поясните принцип работы цифро-аналогового преобразователя.
6. Поясните назначение и условное обозначение аналого-цифрового преобразователя, назначение выводов АЦП.
7. Поясните принцип работы аналого-цифрового преобразователя последовательного типа.
8. Поясните принцип работы аналого-цифрового преобразователя параллельного типа.
Лабораторная работа №30 исследование четырехразрядного параллельного сумматора
30.1. Цель работы
1. Изучить правила сложения и вычитания чисел в двоичной системе счисления.
2. Изучить назначение, структуру и принцип работы сумматоров.
30.2. Теоретические сведения
В двоичном коде над числами можно осуществлять любые арифметические операции: сложение, вычитание, умножение, деление.
Сложение двух двоичных чисел производится аналогично сложению десятичных чисел.
Рассмотрим, например, сложение двух 4-разрядных двоичных чисел. Пусть надо сложить число 0111 (десятичное 7) и 1011 (десятичное 11):
![]()
При сложении 0 и 0 получаем 0, при сложении 1 и 0 получаем 1, при сложении 1 и 1 получаем 0 и перенос в следующий разряд 1. Результат — 10010 (десятичное 18). При сложении любых двух n-разрядных двоичных чисел может получиться n-разрядное или (n+1)-разрядное число.
При вычитании возможно получение отрицательных чисел, поэтому необходимо использовать двоичное представление отрицательных чисел.
Для одновременного представления как двоичных положительных, так и двоичных отрицательных чисел чаще всего используется так называемый дополнительный код. Отрицательные числа в этом коде выражаются таким числом, которое, будучи сложено с положительным числом такой же величины, даст в результате нуль. Для того чтобы получить отрицательное число, надо поменять все биты такого же положительного числа на противоположные (0 на 1, 1 на 0) и прибавить к младшему значащему разряду 1. Например, запишем число –5. Число 5 в двоичном коде выглядит 0101. Заменяем биты на противоположные: 1010 и прибавляем единицу: 1011. Суммируем результат с исходным числом: 1011 + 0101 = 0000. Перенос в пятый разряд игнорируется, поскольку разность не может иметь большее число разрядов, чем уменьшаемое и вычитаемое.
Сумматор – это блок арифметического устройства, выполняющий сложение двоичных чисел.
Сумматор
двух двоичных одноразрядных чисел
называется
полусумматором.
Полусумматор служит основой для создания
сумматоров многоразрядных чисел. Входные
сигналы полусумматора поступают на два
входа
![]() и
.
Выходными сигналами являются сумма S
и перенос в старший разряд P.
Таблица истинности полусумматора
показана на рисунке 30.1, а. Данной таблице
соответствуют логические функции суммы
и переноса в старший разряд соответственно
вида
и
.
Выходными сигналами являются сумма S
и перенос в старший разряд P.
Таблица истинности полусумматора
показана на рисунке 30.1, а. Данной таблице
соответствуют логические функции суммы
и переноса в старший разряд соответственно
вида
![]() ,
,
![]() .
(30.1)
.
(30.1)
Как следует из первой формулы (30.1), функция суммы реализуется с помощью элемента «ИСКЛЮЧАЮЩЕЕ ИЛИ», а функция переноса посредством элемента «И». Функциональная схема полусумматора и его условное обозначение показаны соответственно на рисунках 30.1, б, в.
С использованием
полусумматоров строят сумматоры,
предназначенные для сложения двух
многоразрядных числе. Условное обозначение
четырехразрядного сумматора показано
на рисунке 30.1, г. Сумматор имеет 8 входов,
на которые подаются четырехразрядные
числа X
(входы
,
,
и
![]() )
и Y
(входы
)
и Y
(входы
![]() ,
,
![]() ,
,
![]() и
и
![]() ),
подлежащие сложению. На вход сумматора
Е
подается сигнал переноса от предыдущих
операций. Сумма S
появляется на выходах
),
подлежащие сложению. На вход сумматора
Е
подается сигнал переноса от предыдущих
операций. Сумма S
появляется на выходах
![]() ,
,
![]() ,
,
![]() и
и
![]() .
Вывод P
представляет собой вывод переноса.
.
Вывод P
представляет собой вывод переноса.
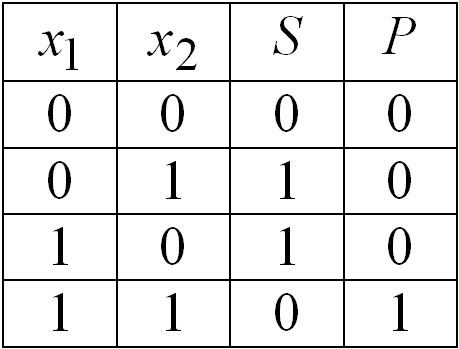
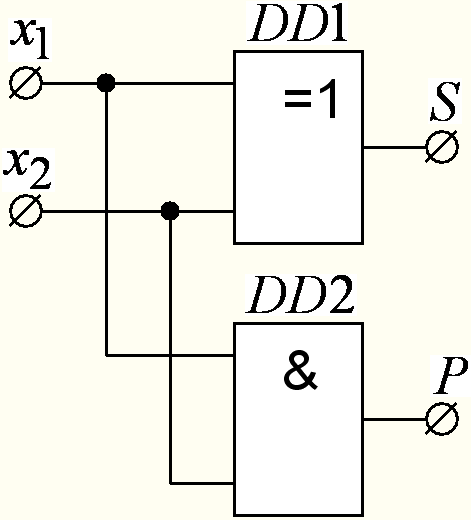

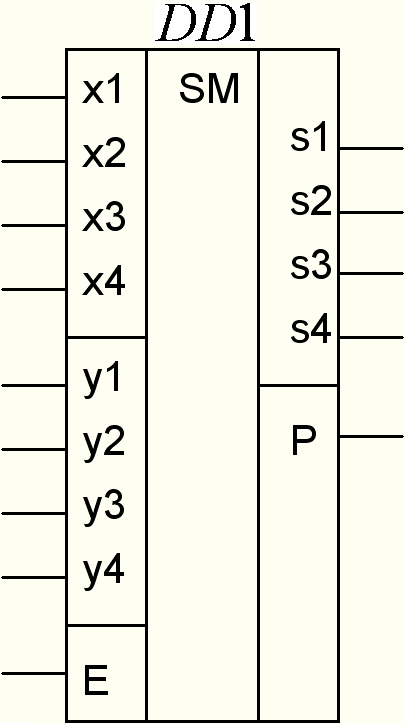
а) б) в) г)
Рисунок 30.1 – Принцип действия и условные обозначения устройств сложения двоичных чисел
