4. Кинематика фотона

Начнем с вывода уравнений движения центра масс фотона. Поскольку центр масс фотона движется в плоскости поляризации и в рамках Аксиомы Единства пространства – материи – времени, то для описания его движения по волновой траектории необходимо иметь два параметрических уравнения.

Так как центр масс фотона движется относительно наблюдателя и относительно геометрического центра модели, то для полного описания такого движения необходимо иметь две системы отсчета (рис. 11): неподвижную и подвижную .

Амплитуда колебаний центра масс фотона будет равна радиусу его вращения относительно геометрического центра фотона. Из рис. 11 имеем [1], [2]

. (90)

Обратим внимание на небольшую величину амплитуды колебаний центра масс фотона в долях длины его волны или радиуса вращения .

Уравнения движения центра масс фотона относительно подвижной системы имеют вид:

; (91)

. (92)

Если фотон движется относительно неподвижной системы отсчета со скоростью , то уравнения такого движения будут иметь вид [1]:

; (93)

. (94)

Итак, главное свойство уравнений (93) и (94), описывающих движение центра масс фотона, заключается в том, что они описывают движение этого центра в рамках Аксиомы Единства пространства – материи – времени. Отметим, что уравнение Луи Де Бройля (55) и уравнение Э. Шредингера (56) этим свойством не обладают. Учитывая соотношения (70), (71), (72) и (90), получим [1], [2]:

(95)

(96)

где

Из этого следует закономерность изменения скорости центра масс фотона, в которую легко вводятся электрическая и магнитная постоянные [1], [2]

(97)

График скорости (97) центра масс фотона показан на рис. 12. Как видно, скорость центра масс фотона действительно изменяется в интервале длины волны или периода колебаний таким образом, что её средняя величина остается постоянной и равной .

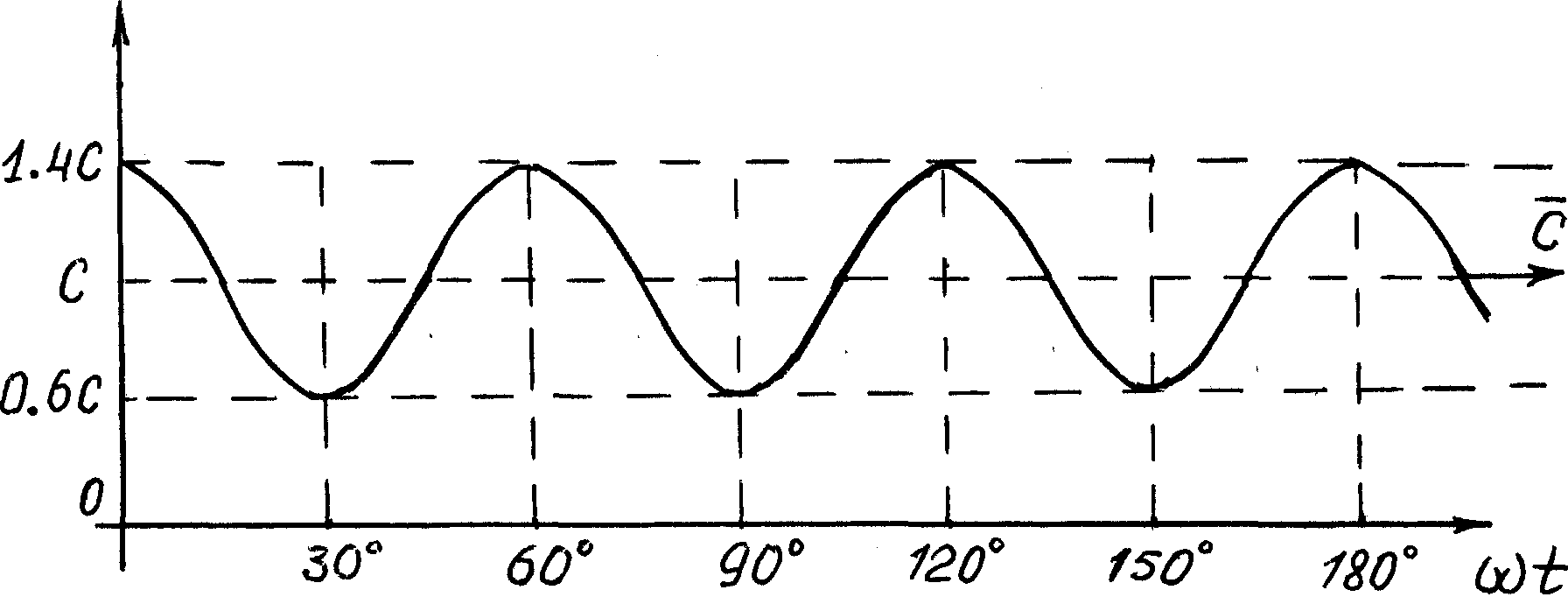
Рис. 12. График скорости центра масс фотона

Уравнения движения центра масс одного из электромагнитных полей фотона относительно подвижной системы отсчета (рис. 11) будут иметь вид:

; (98)

. (99)

Уравнения абсолютного движения центра масс одного электромагнитного поля фотона, то есть движение относительно неподвижной системы отсчета принимают вид:

; (100)

. (101)

Эти уравнения позволяют легко определить все кинематические характеристики центров масс электромагнитных полей фотона [1], [2].

Итак, мы получили уравнения (95) и (96), которые точнее уравнения Луи Де Бройля (55) и уравнения (56) Шредингера описывают движение фотона. Однако если появляются более точные математические соотношения для описания поведения какого-либо объекта, то менее точные обязательно должны содержаться в них и быть их следствиями. Этому требованию полностью отвечают соотношения (93) и (94), описывающие движение центра масс фотона.

Чтобы получить волновое уравнение (55), надо вывести процесс описания движения центра масс фотона за рамки Аксиомы Единства пространства - материи - времени. Для этого надо взять одно из уравнений (93), (94), например, уравнение (94). Обращаем внимание читателя на то, что эта операция автоматически выводит процесс описания движения центра масс фотона за рамки Аксиомы Единства пространства - материи - времени.

. (102)

Чтобы привести это уравнение к виду (55), необходимо ввести в него координату , используя для этого разность фаз.

. (103)

Учитывая что, и , имеем

.

Обозначим:

тогда

(104)

Теперь видно, что основная причина теоретического расползания волнового пакета Луи Де Бройля - независимость координаты от времени и отсутствие соответствия волнового уравнения Де Бройля Аксиоме Единства пространства - материи - времени. Уравнения (93) и (94) лишены этого недостатка.

Нетрудно показать, что уравнение (104) легко приводится к уравнению Шредингера (56) [1], [2]. Для этого выразим из формул (77), (83) частоту и длину волны .

, (105)

. (106)

Введем новое обозначение функции (104) и подставим в неё значения (105) и (106).

(107)

При фиксированном смещение является гармонической функцией времени, а при фиксированном - координаты .

Дифференцируя уравнение (107) дважды по , найдем

(108)

Если с помощью соотношения (108) описывать поведение электрона в атоме, то надо учесть, что его кинетическая энергия и импульс связаны соотношением

. (109)

Откуда

. (110)

Подставляя результат (110) в уравнение (108), имеем

(111)

Известно, что полная энергия электрона равна сумме кинетической и потенциальной энергиям, то есть

. (112)

С учетом этого уравнение (108) принимает вид дифференциального уравнения (56) Э. Шредингера.

(113)

Из изложенного следует, что результат решения уравнения (56) есть функция (104), работающая за рамками Аксиомы Единства пространства – материи – времени.

Таким образом, мы вывели все, постулированные раннее математические модели квантовой механики, описывающие поведение фотона. Мы показали, что уравнение Луи Де Бройля (55) и уравнение Шредингера (56) работают за рамками Аксиомы Единства пространства - материи - времени.

Итак, мы оставляем в покое все математические формулы, которые давно применяют для описания поведения фотона. В этом смысле у нас нет ничего нового, мы только подтвердили достоверность этих формул и дополнили их уравнениями (95) и (96), описывающими движение центра масс фотона в рамках Аксиомы Единства пространства – материи – времени.

Теперь у нас есть основания назвать фотоном локализованное в пространстве электромагнитное образование, из которого формируется не электромагнитное, а фотонное излучение, переносящее в пространстве энергию и информацию [1], [2]. Поэтому у нас есть основание считать фотон элементарным носителем информации и энергии.