Характеристика позиций

Для каждой позиции вводится характеристика. Характеристикаd_iпозицийiбазируется на понятии “расстояние”. В общем случае расстояние между позициямиiиjобозначимd_ij. В свою очередь расстояние между позициями определяется принятой метрикой определения расстояния.

При этом используется два подхода.

1. Кратчайшее расстояние между двумя точками по прямой в рамках евклидовой геометрии. В этом случае расстояние d_ijопределяется по правилам прямоугольного треугольника как показано на рис. 5.7.

Рис. 5.7. Эвклидова метрика

2. Расстояние в понятиях ортогональной метрики. В этом случае коммутационное поле покрывается ортогональной сеткой, в узлах которой расположены позиции. Расстояние вычисляется только вдоль линий этой сетки d_ij=h_x +h_y, гдеh_xиh_yразность координат по осямxиyсоответственно для точекiиj(рис. 5.8).

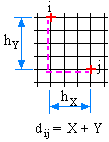
Рис. 5.8. Ортогональная метрика

Какие особенности имеет ортогональная метрика, и в чём её преимущество? Во-первых, это простота вычислений. Вместо четырёх математических операций (при расчёте расстояния по евклидовой геометрии), три из которых не тривиальные, выполняется одна. Во-вторых, в ортогональной метрике расстояние не зависит от конкретного маршрута между точками (при кратчайших маршрутах). В автоматизированных системах для экономии вычислительных ресурсов при проектировании печатных плат обычно предпочтение отдаётся ортогональной метрике. При проектировании проводного монтажа применяются обе системы измерения расстояния.

Характеристика позицийвычисляется по матрице расстоянийDкоммутационного поля. Столбцы и строки матрицы соответствуют позициям коммутационного поля. Элементы матрицыd_ijесть расстояния между соответствующими позициями. Диагональ остаётся нулевой.

Для примера приведена матрица (рис. 5.9) расстояний некоторого коммутационного поля, имеющего 9 позиций (см. рис. 5.6). Эти позиции расположены в узлах координатной сетки. Для простоты примем шаг сетки по оси xравным шагу по осиy. Мера расстоянияшаг сетки, принимаемый за единицу.

Характеристика d_iпозицииiестьсуммарноерасстояние от неё до всех остальных позиций. Для вычисления характеристики удобно использовать матрицу расстояний. Суммируя все элементы строки для позицииi, получаем ее характеристикуd_i.

Среди всех позиций определяется центральная позиция. Центральная позицияэто позиция, для которой значение характеристики минимальное. В общем случае может быть одна или несколько центральных позиций. В нашем примере центральной позицией является позиция 5, для которой характеристика равна 12минимальное значение из всех.

Рис. 5.9. Пример матрицы расстояний D коммутационного поля

Параллельный алгоритм одновременного размещения

Следующий шаг – решение задачи размещения. Суть задачи состоит в размещении вершин графа на заданных позициях коммутационного поля, т.е. надо указать какая вершина на какой позиции должна быть установлена. Очевидно, что число вершин графа не должно быть больше числа позиций коммутационного поля. Для этого используется ряд алгоритмов, среди которых выделяется простотой и эффективностьюпараллельный алгоритм обратного размещения. Он может быть использован в ручном варианте решения даже нетривиальных задач размещения.

Для реализации алгоритма задаётся матрица соединений для графа и матрица расстояний для коммутационного поля.

По матрице соединений подсчитывают степени вершин и далее ранжируются вершины по возрастанию их степени:

r(X₁) <r(X₂) <r(X₃) < ... <r(X_N).

В данном случае индексы 1, 2, 3, ... , Nобозначают не номера вершин в графе, а их порядок в соответствии с возрастанием степени вершины.

На следующем шаге по матрице расстояний коммутационного поля подсчитывают характеристики позиций и ранжируются их в порядке убывания:

d₁>d₂>d₃> ... >d_N, гдеd_N- центральная позиция.

В данной записи смысл нижних индексов аналогичен, отмеченному выше.

В большинстве случаев число вершин задаётся равным числу позиций коммутационного поля (в любом случае не больше).

Назначение позиций для каждой вершины проводится следующим образом: сопоставляются два ранжированных ряда, полученных выше, и вершина X₁ставится на позициюd₁, вершинаX₂на позициюd₂и т.д. Таким образом, осуществляется одновременное размещение вершин графа на позициях коммутационного поля.

Замечания к алгоритму:

Алгоритм создаёт хорошие предпосылки для качественного выполнения этапа трассировки.

Во многих случаях некоторые позиции платы уже “забронированы” под определённые компоненты (например, установка соединителя на краю платы). Поэтому алгоритм претерпевает изменения. В этом случае реализуется идея размещения по связности элементов: на фиксированные позиции ставится определенный элемент, а далее – чем больше следующий элемент связан с установленным, тем ближе к нему размещается.