Тема 2. Моделювання поведінки споживача

1. Кардинальний вимір корисності

2. Ординарний вимір корисності

3. Нетранзитивні переваги

Нехай є n видів товарів та послуг та визначено доход споживача D або його частину, яку він витрачає на придбання товарів та послуг, а також ціни на них. Потрібно визначити, які товари у якій кількості він куплятиме?

Побудові моделі передують певні припущення щодо вибору споживача.

Припущення: 1) вибір - одномоментний; 2) незалежний від попередньо зробленого; 3) бюджетне обмеження – жорстке.

Змінні моделі: x₁, x₂, … x_n – кількість товарів та послуг кожного з n видів, які придбає споживач. Тобі бюджетне обмеження набуває вигляду:

,

де і – номер виду товару чи послуги, р_i - ціна і-го товару (послуги). Це обмеження та умови невід’ємності: , створять множину Х припустимих рішень споживача. Яке меню споживання вибере споживач з цієї множини? Певно, те, яке для нього краще. Існує декілька підходів до формалізації поняття “краще”. Розглянемо деякі з них.

І. Функція корисності U (x₁,…, x_n) = U (x). Це така функція, що U(x⁽¹⁾) ≥ U(x⁽²⁾), якщо меню споживання x⁽¹⁾ не гірше від x⁽²⁾. Припускаємо, що така функція корисності існує, тоді найкраще меню споживання – точка максимуму функції U(x) на X:

U (x) → max,

, (2.1)

, .

Модель (2.1) зветься моделлю поведінки споживача з кардинальним виміром корисності. Бажані властивості U(x):

1. Неперервність (навіть у функції, що має розриви першого роду, max та min можуть не існувати, а sup та inf можуть досягатися при прямуванні до однієї точки ):

U(x)

x

За такої ситуації не зрозуміло, як визначити розв’язок задачі (2.1).

2. Опуклість догори (за її відсутності не зрозуміло, як трактувати локальні екстремуми для (2.1)).

3 . Диференційованість. - щоб легше застосовувати

4. Монотонність. математичні методи

З а цих властивостей U(x) розв‘язок х^* задачі (2.1) має задовольняти умовам:

, якщо (2.2)

, якщо ,

.

З монотонності U(x) випливає, що

, тому

хоча б для одного і та

, звідси та

,

Додатніми будуть тільки ті компоненти вектору х^*, для яких . Величину можна інтерпретувати як міру привабливості товару і для споживача. Споживатимуться лише ті товари, для яких міра привабливості набуває найбільших значень.

З цієї умови, рівняння та умов невід’ємності іноді можна знайти х^*. Нехай, наприклад,

Тоді очевидно, що всі (інакше U(x) прямуватиме до - ∞). Звідси

, ,

або ж для будь-яких і та j, , . Взявши j = 1, одержимо

або ж

, .

Підставивши одержаний вираз до рівняння

,

маємо

.

Звідси

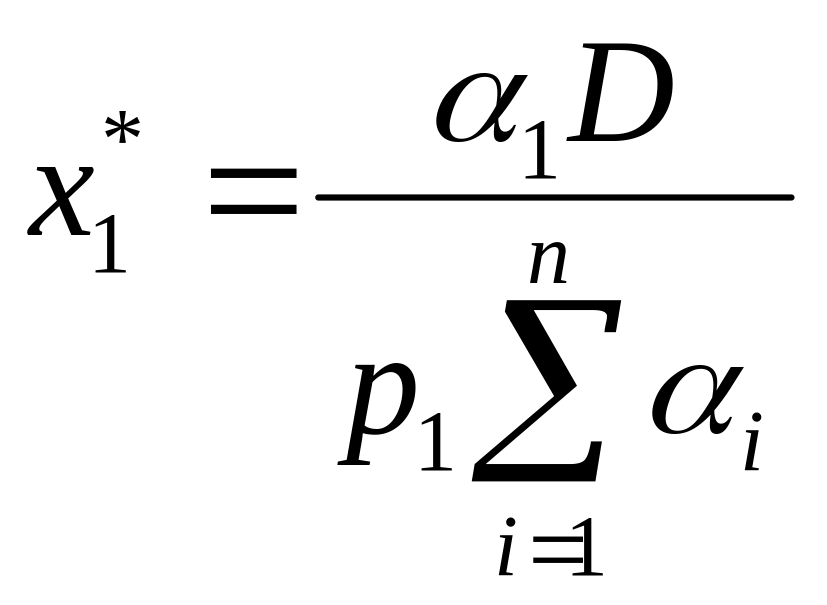
та

, .

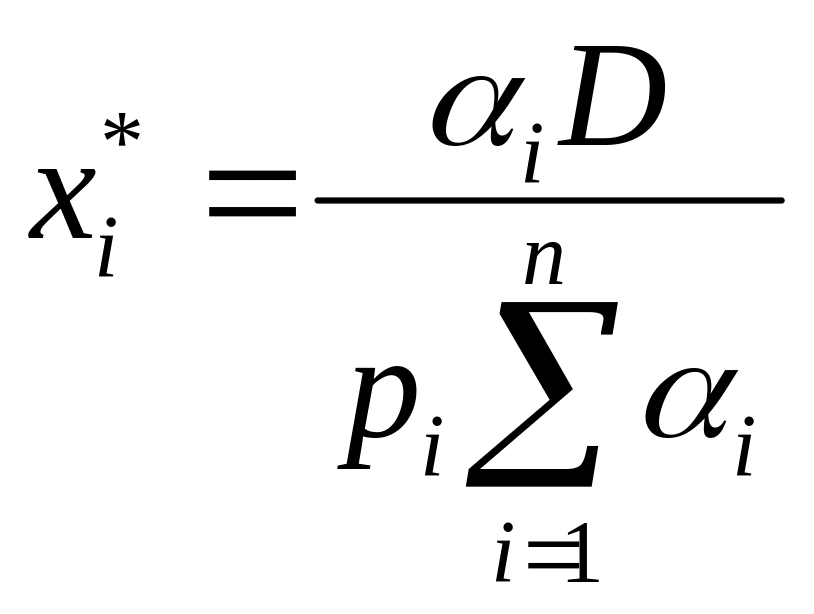ІІ Бінарні відношення R (множина впорядкованих пар меню споживання)

- множина припустимих меню (споживацьких наборів), R – відношення переваг споживача (відношення типу “не гірше”).

Т реба знайти таке , що V виконується . Для існування х^* необхідне виконання таких умов:

1 . Повнота: V х⁽¹⁾, х⁽²⁾ має виконуватись або х⁽¹⁾ Rx⁽²⁾, або х⁽²⁾ Rx⁽¹⁾, або і те, і інше (тоді х⁽¹⁾ та х⁽²⁾ звуться еквівалентними, що позначається ). Відношення R є об’єднанням відношення еквівалентності та відношення строгої переваги .

2 . Рефлексивність: V х виконується .

3. Транзитивність: якщо для довільних х⁽¹⁾, х⁽²⁾, х⁽³⁾ виконується х⁽¹⁾ Rx⁽²⁾, х⁽²⁾ Rx⁽³⁾, то має також виконуватись х⁽¹⁾ Rx⁽³⁾.

4. Неперервність: для будь-яких меню споживання у та z множини {x: xRy} та {x: zRx} – замкнені.

Зауважимо, що перші 3 умови мають, передусім, економічний зміст. У той же час остання умова – здебільше математична (аналогія – неперервність функції корисності).

За зазначених умов існує індекс корисності – функція ν (х): х⁽¹⁾ Rx⁽²⁾ ↔ ν (х⁽¹⁾) ≥ ν (х⁽²⁾) та задача пошуку х^* еквівалентна оптимізаційній задачі

ν (х) → max,

(p, x) ≤ D,

x ≥ 0.

Тут спостерігається повна аналогія з кардинальним виміром корисності!

Дещо відмінною є ситуація, коли не виконуються раніш зроблені припущення щодо властивостей бінарного відношення R. Передусім, це стосується транзитивності. Переваги реальних споживачів вочевидь є рефлексивними, якщо ж відношення R не повне, його можна замінити відношенням R₁: x⁽¹⁾R₁x⁽²⁾ , якщо або x⁽¹⁾Rx⁽²⁾ , або x⁽¹⁾ та x⁽²⁾ неможливо порівняти. Відношення R₁ буде повним, а меню споживання x⁽¹⁾ та x⁽²⁾ , такі, що не виконується ані x⁽¹⁾Rx⁽²⁾ , ані x⁽²⁾Rx⁽¹⁾ , будуть еквівалентними за цим відношенням.

Невиконання умови транзитивності означає, що існують такі x⁽¹⁾, x⁽²⁾ , x⁽³⁾, що , x⁽²⁾Rx⁽³⁾, проте x⁽³⁾Rx⁽¹⁾. За цих умов не існує індекса корисності, породженого R, бо ні для якої функції V(x) не можуть одночасно виконуватись нерівності

V (x⁽¹⁾) > V (x⁽²⁾), V (x⁽²⁾) ≥ V (x⁽³⁾), та V (x⁽³⁾) ≥ V (x⁽¹⁾).

Для формалізації нетранзитивних відношень потрібно застосовувати інший інструментарій, наприклад, індикатор переваг.

Індикатором переваг зветься така функція h (x⁽¹⁾, x⁽²⁾), що h (x⁽¹⁾, x⁽²⁾) > 0, коли ,

h (x⁽¹⁾, x⁽²⁾) < 0, коли ,

h (x⁽¹⁾, x⁽²⁾) = 0, коли .

Очевидно, що таку функцію можна побудувати для будь-якого відношення R, поклавши, що вона дорівнює 1, 0, -1 для трьох раніше розглянутих випадків. Іноді нетранзитивні переваги вдається описати за допомогою неперервних індикаторів, наприклад, нехай x⁽¹⁾ та x⁽²⁾ - це дійсні числа, а функція h (x⁽¹⁾, x⁽²⁾) визначена наступним чином:

h (x⁽¹⁾, x⁽²⁾) = x⁽¹⁾ x⁽²⁾ (|x⁽¹⁾| - | x⁽²⁾|).

Тоді для x⁽¹⁾ = 3, x⁽²⁾ = 1, x⁽³⁾ = -2 буде виконуватись:

h (x⁽¹⁾, x⁽²⁾) = 6 > 0, h (x⁽²⁾, x⁽³⁾) = 2 > 0,

h (x⁽³⁾, x⁽¹⁾) = 6 > 0,

що відповідає порушенню умови транзитивності для цих розв’язків.

Задача пошуку х^* (якщо такий елемент існує) може бути сформульована за допомогою індикатора переваг наступним чином.

Треба знайти таке х^* Х, що для будь-якого х Х буде виконуватись h (х^*, x) ≥ 0. Остання нерівність еквівалентна виконанню умови

.

Знайти таке х^* можна, максимізувавши функцію φ(х^*) на множині Х. Якщо - найкраще меню споживання існує. Якщо ж , тоді для будь-якого меню споживання існуватиме інше допустиме меню, яке переважає його. Проте й у цьому випадку як споживчий вибір можна розглядати таке х^*, яке буде максимізувати φ(х^*) або ж деякі інші функції, наприклад

,

або

.

Тут α(х) – деяка вагова функція, така, що .

При цьому виникатиме деяка невизначеність, пов’язана з вибором, оскільки за різних функцій α(х) та за різних критеріїв як найкращі будуть обрані різні меню споживання. Проте для кожного правила вибору можна довести виконання властивостей х^*, подібних до тих, які були одержані при кардинальному вимірюванні корисності (тільки гранична корисність для кожного з цих правил буде визначатися окремо).