Тема 10. Комплексні макроекономічні моделі

1. Модель Хікса-Хансена.

2. Класична модель.

3. Кейнсіанська модель та її модифікації.

4. Динамічна макромодель перехідної економіки.

Раніш розглянуті макромоделі відображають окремі економічні процеси - зміни реальних значень макроекономічних показників, зміну цін, тощо. При дослідженні макроекономічних процесів виникає потреба одночасного, узгодженого розгляду різних сегментів національного ринку та різнопланових явищ, які на них відбуваються. Для цього розроблені комплексні макроекономічні моделі. Розглянемо деякі з них.

У моделі Хікса-Хансена розглянуто реальний сектор та ринок робочої сили. Для опису реального сектора застосовано модель IS-LM:

Y = min (kI(i)), max (0, ),

де Y – величина реального ВВП, I(i) – функція інвестиційного попиту, і – норма процента (середня кредитна ставка), M₂(i) – спекулятивний попит на гроші, M^S - пропозиція грошей. Коефіцієнт τ визначає швидкість обертання грошей та наявність власних вільних коштів у суб’єктів господарювання, k – фондоємність виробництва.

Фактично, це – залежність обсягу створеного ВВП Y від існуючих фінансових обмежень.

Як правило, використовуються наступні залежності:

,

де I_m - найбільший обсяг інвестицій, якого можна досягнути за нульових значень кредитної ставки (технологічна потреба у інвестиціях).

Тут функція інвестиційного попиту вважається подібною до функції попиту на товари першої необхідності з обмеженим граничним споживанням, α₁ та α₂ –її коефіцієнти;

,

де - рівень “ліквідної пастки” – відсоток гарантованих доходів по високонадійним спекулятивним операціям (наприклад, операціям з державними цінними паперами).

Взаємозв’язок між реальним сектором та ринком робочої сили визначається за допомогою виробничої функції

Y = F(L).

Це може бути відома функція типу Коба-Дугласа:

Y = a₀ L^γ , 0 < γ < 1,

де а₀ – коефіцієнт (залежить від наявного капіталу), або ж інша залежність.

Ринок робочої сили визначається кривими попиту на працю та пропозиції праці:

L^D = G₁ (W),

L^S = G₂ (W),

де W – реальна оплата праці (ціна робочої сили). Найчастіше вважається, що

, C₀, C₁ > 0 ,

0 , якщо W ≤ W₀,

G₂ (W) =

C₂ (W – W₀) , якщо W > W₀,

де С₂ > 0 , 0 < C₃ < 1 – коефіцієнти (параметри) функцій попиту та пропозиції.

Типові схеми розрахунків за моделлю Хікса-Хансена (рис. 10.1):

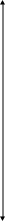
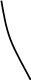i

IS

LM

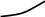
W W₀ y^*

y

L^*

L^D

L^S L y = F (L)

Рис. 10.1

І. Знаходимо стан рівноваги (ситуацію повної зайнятості – не плутати з повним використанням вільних трудових ресурсів!) з рівняння

L^* = G₁ (W) = G₂ (W).

Підставивши L^* до виробничої функції, знайдемо ВВП, що їй відповідає:

y^* = F (L^*) .

Порівняємо значення y^* з найбільш досяжним значенням ВВП за наявних фінансових обмежень. Останнє визначається із співвідношення:

,

йому відповідатиме рівноважна норма відсотку .

Якщо (як це показано на рис. 10.1) рівноваги на ринку праці не можна досягти за наявних фінансових ресурсів, потрібно змінювати параметри моделі IS-LM (перш за все, M^S та ), або погодитись на додаткове безробіття.

Якщо - рівновага на ринку праці досягається за рахунок відсутності фінансової рівноваги. При цьому норма проценту має бути у межах [i₁ , i₂], де i₁ – розв’язок рівняння , i₂ - розв’язок рівняння y^* = kI (i).

Якщо , то досягнуто узгодженої фінансової рівноваги та рівноваги на ринку праці.

ІІ. Фіксуємо певне значення ВВП (ним, зокрема, може бути - найбільше досяжне значення ВВП). З рівняння

= F(L)

визначаємо потребу у трудових ресурсах L . Підставивши це значення до рівняння

L^D = G₁(W) = L,

знаходимо відповідний рівень оплати праці .