леции-Деменко(2 семестр) / Lma2s-7

27

Элементарные асимптотические методы.

Асимптотическое представление функций.

В этом разделе мы будем изучать поведение функции, определенной в при . Нас будут интересовать функции, имеющие сложный вид, и мы будем сравнивать их поведение с поведением других функций, более простой природы.

Вспомним некоторые определения и формулировки теорем, встречавшихся нам ранее.

Определение. Говорят, что функция есть бесконечно малая по сравнению с функцией при и пишут , если , где - бесконечно малая функция при .

Определение. Запись

означает, что

,

где - ограниченная функция в некоторой окрестности или проколотой окрестности .

Определение. Говорят, что функции и эквивалентны при и пишут , если , где - бесконечно малая функция при .

Нам известны также следующие свойства выражений, содержащих :

Утверждение.

.

Теорема. Пусть непрерывные в нуле функции и эквивалентны при , а функция бесконечно малая при .

Тогда функция будет эквивалентна функции при .

Аналогично предыдущей доказывается теорема:

Теорема. Пусть , где при . И пусть - бесконечно малая при , причем в .

Тогда при .

Приведем асимптотические представления для основных элементарных функций при :

,

,,,.

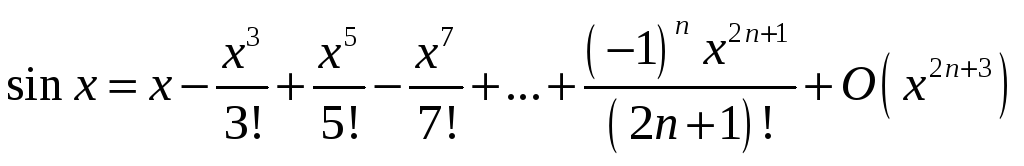Разберем несколько примеров.

Пример 1. Написать асимптотическую формулу для при (записать два члена асимптотики, не считая остатка).

Решение. , где - бесконечно малая при ,

.

Пример 2. Написать асимптотическую формулу для при (записать два члена асимптотики, не считая остатка).

Решение.

, где - бесконечно малая при ;

.

Пример 3. Написать асимптотическую формулу для при (записать два члена асимптотики, не считая остатка).

Решение.

;

(все остальные слагаемые в последнем произведении «поглощены» ). Таким образом

.

Асимптотика корней уравнения.

Пример 4. Используя формулу Тейлора, найти асимптотику корней уравнения (записать два члена асимптотики, не считая остатка).

Решение. Обозначим через последовательность корней нашего уравнения. Из свойств функций и видно, что , где - бесконечно малая последовательность. Для наших целей формулу Тейлора достаточно применить в форме эквивалентности, а именно:

, и . Тогда . Получаем .

Асимптотические формулы для функций, заданных в виде интегралов.

Пусть функция непрерывна на полуоси . Нас будет интересовать поведение функции при .

Теорема. Пусть положительные функции , непрерывны на полуоси . Обозначим , .

Тогда если и при , то при .

Доказательство. Пусть . Согласно условию теоремы, интеграл расходится, поэтому по теореме сравнения для несобственных интегралов расходится также и интеграл , то есть . Следовательно, при нахождении предела отношения функций и мы можем воспользоваться правилом Бернулли-Лопиталя. Итак, получаем

.

Пусть теперь . Если интеграл сходится, то существует конечный предел и . Если же , то воспользуемся правилом Бернулли-Лопиталя:

.

Во всех случаях .

Пример 5. Написать асимптотическое представление функции, заданной интегралом: (записать два члена асимптотики).

Здесь ,

.

Пример 6. Написать асимптотическое представление функции, заданной интегралом: (записать два члена асимптотики).

Воспользуемся формулой интегрирования по частям:

,

.

Так как , то и . Это означает, что и . Окончательно получаем

.

Докажем еще одну теорему:

Теорема. Пусть положительные функции , непрерывны на полуоси . Обозначим , .

Тогда если сходится и при , то при .

Доказательство. Пусть . Согласно условию теоремы, интеграл сходится, поэтому по теореме сравнения для несобственных интегралов сходится также и интеграл , то есть , то есть . Следовательно, при нахождении предела отношения функций и мы можем воспользоваться правилом Бернулли-Лопиталя. Итак, получаем

.

Пусть теперь . Очевидно, что интеграл сходится, то есть , поэтому мы можем воспользоваться правилом Бернулли-Лопиталя:

.

Пример 7. Написать асимптотическое представление функции, заданной интегралом: (записать два члена асимптотики).

.

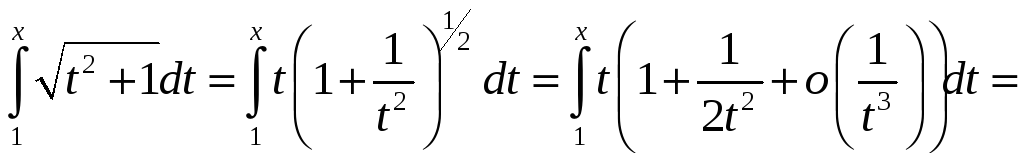
Поскольку константа нам неизвестна, мы можем только записать

.