леции-Деменко(2 семестр) / Lma2s-5

18

Геометрические приложения определенного интеграла.

Длина плоской кривой.

Длина кривой, заданной параметрически.

Определение. Длиной кривой называется точная верхняя граница для множества периметров вписанных в кривую ломаных: . Если это число конечно, то кривая называется спрямляемой.

Рассмотрим параметрически заданную гладкую кривую

.

Утверждение. Параметрически заданная на конечном промежутке гладкая кривая спрямляема.

Доказательство. Поскольку функции и непрерывны на отрезке, то они ограничены на нем, то есть

.

Рассмотрим ломаную с вершинами в точках . Периметр ломаной равен

.

Мы воспользовались формулой Лагранжа для конечных приращений и ограниченностью производных на отрезке .

Видим, что множество периметров вписанных ломаных ограничено, следовательно, кривая спрямляема. Аналогично оценке сверху, мы можем получить и оценку снизу для длины нашей кривой. Запишем:

.

Формула дли вычисления длины дуги гладкой кривой, заданной параметрически.

Введем функцию , равную длине переменной дуги от точки до .

Рассмотрим промежуток . Приращение равно длине дуги, заданной на отрезке . Запишем оценку для приращения длины на этом промежутке:

.

Здесь , соответственно, наибольшие и наименьшие значения модулей производных и на отрезке . Из непрерывности производных вытекает, что

.

То есть

.

Таким образом, длина переменной дуги – дифференцируемая функция, и по формуле Ньютона-Лейбница ее приращение на отрезке равно

. (1)

Пример 1. Найти длину одной арки циклоиды

.

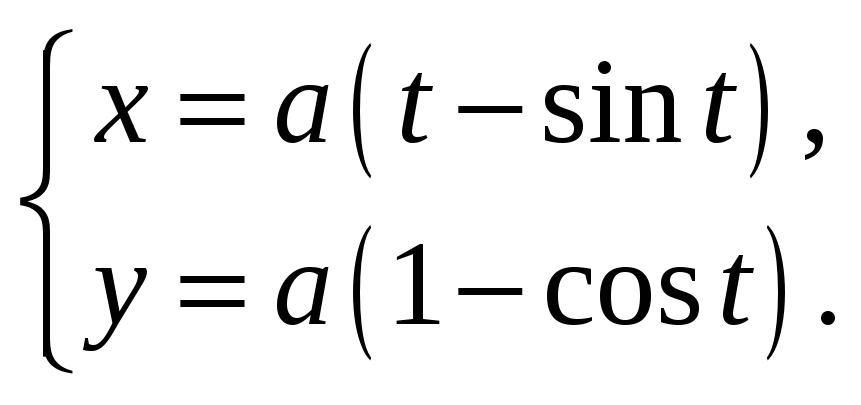
Решение:

.

Длина кривой, заданной явно.

Пусть кривая задана явно в прямоугольных координатах:

.

Принимая за параметр, ее можно записать в параметрическом виде: Применив (1), получим

.

Пример 2. Найти длину дуги кривой от до .

Решение: .

Длина кривой, заданной в полярных координатах.

Если кривая задана в полярных координатах , то ее можно задать параметрически системой

В этом случае

.

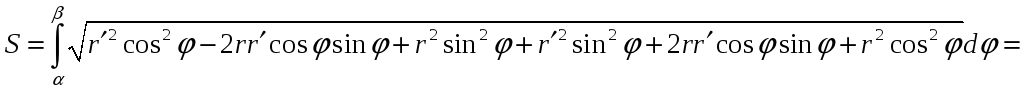
Пример 3. Найти длину дуги окружности .

Решение: .

Площадь плоской фигуры.

Пусть - произвольная фигура на плоскости. Обозначим через Многоугольники, целиком содержащиеся в , а через - многоугольники, содержащие . Через и обозначим их площади. Имеем . Ограниченное сверху множество чисел имеет точную верхнюю грань , а ограниченное снизу

Множество чисел точную нижнюю грань . Очевидно, что , если же эти числа совпадают, то общее их значение называют площадью фигуры , а саму эту фигуру называют квадрируемой.

Площадь криволинейной трапеции.

Пусть - неотрицательная интегрируемая функция, заданная на отрезке . Рассмотрим криволинейную трапецию , определенную неравенствами: . Верхние суммы Дарбу для являются площадями многоугольников, содержащих , а, соответственно, нижние – площадями многоугольников, целиком содержащихся в . Таким образом, получаем

. Из интегрируемости на отрезке следует, что , а, значит, фигура квадрируема и

.

Если функция отрицательна, то интеграл равен площади, взятой со знаком минус, если же меняет знак, то равен алгебраической сумме площадей.

Если криволинейная трапеция снизу и сверху ограничена кривыми

и ,

то площадь такой трапеции будет равна

.

Пример 4. Найти площадь области, ограниченной кривыми и .

Решение: .

Площадь фигуры, заданной в полярных координатах.

Найдем площадь сектора , ограниченного непрерывной кривой и двумя полупрямыми и . Рассмотрим разбиение отрезка - и проведем соответствующие этим углам радиус-векторы. Пусть и соответственно наибольшее и наименьшее значение функции в промежутке . Площадь множества круговых секторов, ограниченных радиус-векторами и целиком содержащихся в, равна , площадь круговых секторов с теми же самыми радиус-векторами, содержащих , равна . Эти числа являются соответственно нижней и верхней суммами Дарбу для интеграла и имеют пределом этот интеграл. Получаем

.

Пример 5. Найти площадь сектора, ограниченного окружностью и лучами и .

Решение: .

Объем тела вращения.

Выведем формулу для вычисления объема тела , полученного при вращении кривой вокруг оси . Для этого разобьем на части плоскостями, перпендикулярными оси и проходящими через точки . Часть содержит в себе цилиндр, в основании которого лежит круг радиуса , а высота равна . Аналогично, содержится в цилиндре с круговым основанием радиуса и той же высотой. Объемы полученных частей будут равны соответственно, и , то есть совпадают с нижней и верхней суммами Дарбу для интеграла . Окончательно получаем

.

Пример 6. Найти объем шара радиуса .

Решение: .