
леции-Деменко(2 семестр) / Lma2s-4
.doc
Свойства определенного интеграла
Пусть функция
![]() интегрируема на отрезке
интегрируема на отрезке
![]()
![]() .
Положим по определению
.
Положим по определению
![]() и
и
![]() .
.
![]() (Аддитивность). Пусть ограниченная
кусочно-непрерывная функция
(Аддитивность). Пусть ограниченная
кусочно-непрерывная функция
![]() определена в наибольшем из промежутков
определена в наибольшем из промежутков
![]() ,
,
![]() и
и
![]() .
Тогда справедливо равенство
.
Тогда справедливо равенство
![]() .
.
Доказательство.
![]() Предположим
сначала, что
Предположим
сначала, что
![]() .
Рассмотрим разбиение отрезка
.
Рассмотрим разбиение отрезка
![]() на части. Не нарушая общности, можно
считать точку
на части. Не нарушая общности, можно
считать точку
![]() одной из точек деления. Для соответствующей
интегральной суммы будем иметь
одной из точек деления. Для соответствующей
интегральной суммы будем иметь
![]() .
.
Переходя к пределу при
![]() ,
получим требуемое равенство.
,
получим требуемое равенство.
Другие случаи взаимного расположения
точек
![]() приводятся к разобранному. Пусть,
например,
приводятся к разобранному. Пусть,
например,
![]() .
Тогда, по доказанному,
.
Тогда, по доказанному,
![]() ,
,
![]() .
.
После перестановки пределов интегрирования в последнем интеграле, получим нужное нам равенство.
Аналогично поступаем с другими
расположениями.![]()
![]() (Линейность).
Пусть функции
(Линейность).
Пусть функции
![]() и
и
![]() интегрируемы на отрезке
интегрируемы на отрезке
![]() .
Тогда произвольная линейная комбинация
.
Тогда произвольная линейная комбинация
![]() этих функций также будет интегрируемой
на этом отрезке, причем
этих функций также будет интегрируемой
на этом отрезке, причем
![]() .
.
Доказательство.
![]() Возьмем
произвольное разбиение
Возьмем
произвольное разбиение
![]() отрезка
отрезка
![]() на части и составим интегральные суммы
для всех трех интегралов. При этом точки
на части и составим интегральные суммы
для всех трех интегралов. При этом точки
![]() в каждом частичном промежутке выбираем
для всех трех сумм одни и те же. Получим
в каждом частичном промежутке выбираем
для всех трех сумм одни и те же. Получим
![]() .
.
Переходя в последнем равенстве к пределу
при
![]() ,
убеждаемся в интегрируемости линейной
комбинации и справедливости требуемого
равенства.
,
убеждаемся в интегрируемости линейной
комбинации и справедливости требуемого
равенства.![]()
![]() Теорема
(об оценке модуля интеграла). Пусть
функция
Теорема
(об оценке модуля интеграла). Пусть
функция
![]() интегрируема на отрезке
интегрируема на отрезке
![]() ,
тогда функция
,
тогда функция
![]() также интегрируема на этом отрезке, и
имеет место неравенство
также интегрируема на этом отрезке, и
имеет место неравенство
 .
.
Доказательство.
![]() Рассмотрим
произвольное разбиение
Рассмотрим
произвольное разбиение
![]() отрезка
отрезка
![]() .
Так как для любой пары точек
.
Так как для любой пары точек
![]() будет
будет
![]() ,
то и колебание
,
то и колебание
![]() функции
функции
![]() в этом промежутке не превосходит
в этом промежутке не превосходит
![]() (колебания функции
(колебания функции
![]() ).
В таком случае имеем
).
В таком случае имеем
![]() ,
а переходя к пределу в последнем
неравенстве при
,
а переходя к пределу в последнем
неравенстве при
![]() ,
убеждаемся в интегрируемости функции
,
убеждаемся в интегрируемости функции
![]() .
Для доказательства нужного нам неравенства
для интегралов перейдем к пределу в
соответствующем неравенстве для
интегральных сумм.
.
Для доказательства нужного нам неравенства
для интегралов перейдем к пределу в
соответствующем неравенстве для
интегральных сумм.![]()
![]() Теорема (об интегрировании неравенств).
Если функции
Теорема (об интегрировании неравенств).
Если функции
![]() и
и![]() интегрируемы на отрезке
интегрируемы на отрезке
![]() и
и
![]() везде на
везде на
![]() ,
то
,
то
![]() .
.
Доказательство.
![]() Так
как функции
Так
как функции
![]() и
и
![]() интегрируемы, то мы можем выбрать любую
последовательность разбиений с
параметрами, стремящимися к нулю, для
того, чтобы в пределе получить интеграл.
Выберем разбиения
интегрируемы, то мы можем выбрать любую
последовательность разбиений с
параметрами, стремящимися к нулю, для
того, чтобы в пределе получить интеграл.
Выберем разбиения
![]() отрезка
отрезка
![]() на
на
![]() равных промежутков:
равных промежутков:
![]() и выделим точки
и выделим точки
![]() .
Тогда, с учетом заданного неравенства,
имеем:
.
Тогда, с учетом заданного неравенства,
имеем:
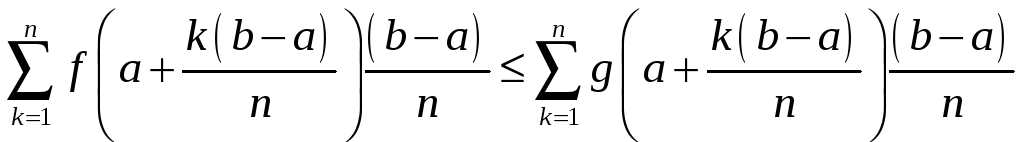 ,
,
и, переходя в последним неравенстве к
пределу при
![]() ,
получаем нужное нам неравенство.
,
получаем нужное нам неравенство.![]()
![]() Теорема (об оценке интеграла). Если
функция
Теорема (об оценке интеграла). Если
функция
![]() интегрируема на отрезке
интегрируема на отрезке
![]() ,
и если на всем этом отрезке справедливо
неравенство
,
и если на всем этом отрезке справедливо
неравенство
![]() ,
то
,
то
![]() .
.
Доказательство.
![]() Воспользуемся
предыдущим свойством с учетом того, что
Воспользуемся
предыдущим свойством с учетом того, что
![]() .
.![]()
Теорема о среднем значении
Определение. Средним интегральным
функции
![]() на отрезке
на отрезке
![]() называется число
называется число
![]() .
.
Теорема (о среднем интегральном).
Пусть функция
![]() интегрируема на отрезке
интегрируема на отрезке
![]() ,
и пусть на всем этом отрезке
,
и пусть на всем этом отрезке
![]() .
Тогда
.
Тогда
![]() ,
,
где
![]() .
.
Доказательство.
![]() По
теореме об оценке интеграла
По
теореме об оценке интеграла
![]() ,
,
откуда получаем
![]() .
.
Теперь полагаем
![]() .
.![]()
В случае непрерывной функции справедлива следующая теорема.
Теорема (о среднем интегральном
значении непрерывной функции). Пусть
функция
![]() непрерывна на отрезке
непрерывна на отрезке
![]() .
Тогда найдется точка
.
Тогда найдется точка
![]() такая, что
такая, что
![]() .
.
Доказательство.
![]() В
качестве
В
качестве
![]() и
и
![]() возьмем соответственно наименьшее и
наибольшее значение функции
возьмем соответственно наименьшее и
наибольшее значение функции
![]() на отрезке
на отрезке
![]() .
По второй теореме Вейерштрасса эти
значения принимаются в некоторых точках
.
По второй теореме Вейерштрасса эти
значения принимаются в некоторых точках
![]() :
:
![]() .
.
По теореме о среднем интегральном
![]() принадлежит отрезку с
принадлежит отрезку с
![]() .
По теореме же Коши о промежуточном
значении непрерывной функции на отрезке
с концами в точках
.
По теореме же Коши о промежуточном
значении непрерывной функции на отрезке
с концами в точках
![]() и
и
![]() найдется точка
найдется точка
![]() ,
в которой
,
в которой
![]() .
.![]()
Требование непрерывности функции
![]() на
на
![]() существенно. В самом деле, рассмотрим
существенно. В самом деле, рассмотрим
![]() Тогда
Тогда
![]() (множеству значений функции
(множеству значений функции
![]() ).
).
Интеграл с переменным верхним пределом
Пусть функция
![]() интегрируема на отрезке
интегрируема на отрезке
![]() .
Определим на этом же отрезке функцию
.
Определим на этом же отрезке функцию
![]() ,
,
которую
часто называют интегралом с переменным
верхним пределом. Из свойства аддитивности
определенного интеграла вытекает
корректность определения функции
![]() для
для
![]() .
.
Теорема
(о непрерывности интеграла с переменным
верхним пределом). Если функция
![]() интегрируема на отрезке
интегрируема на отрезке
![]() ,
то функция
,
то функция
![]() будет непрерывной на этом отрезке.
будет непрерывной на этом отрезке.
Доказательство.
![]() Интегрируемая
на отрезке функция ограничена на нем,
то есть существует такое число
Интегрируемая
на отрезке функция ограничена на нем,
то есть существует такое число
![]() ,
что
,
что
![]() на
на
![]() .
Пусть
.
Пусть
![]() ,
и пусть
,
и пусть
![]() - приращение независимой переменной,
при котором
- приращение независимой переменной,
при котором
![]() .
Воспользовавшись свойством аддитивности,
а также теоремами об оценках определенного
интеграла, получим
.
Воспользовавшись свойством аддитивности,
а также теоремами об оценках определенного
интеграла, получим
 .
.
То
есть
![]() ,
что означает непрерывность функции
,
что означает непрерывность функции
![]() в точке
в точке
![]() .
.![]()
Теорема
(о дифференцируемости интеграла с
переменным верхним пределом). Пусть
функция
![]() непрерывна на отрезке
непрерывна на отрезке
![]() .
Тогда функция
.
Тогда функция
![]() будет дифференцируемой на этом отрезке.
будет дифференцируемой на этом отрезке.
Доказательство.![]()
![]() ,
,
где
![]() лежит между
лежит между
![]() и
и
![]() .
Из непрерывности
.
Из непрерывности
![]() следует, что при
следует, что при
![]() будет справедливо
будет справедливо
![]() .
.![]()
Основная формула интегрального исчисления.
Доказанная
выше теорема означает, что для непрерывной
на
![]() функции
функции
![]() интеграл
интеграл
![]() будет первообразной функцией. Если
будет первообразной функцией. Если
![]() какая-либо другая первообразная
какая-либо другая первообразная
![]() ,
то
,
то
![]() .
Имеем
.
Имеем
![]() ,
,
поэтому
![]() .
При
.
При
![]() получим
получим
![]() .
.
Это - формула Ньютона-Лейбница, - основная формула интегрального исчисления.
Теперь мы можем вычислять определенный интеграл, не используя интегральные суммы.
Пример
1.
 .
.
Пример
2. Найдем среднее интегральное значение
функции
![]() на отрезке
на отрезке
![]()
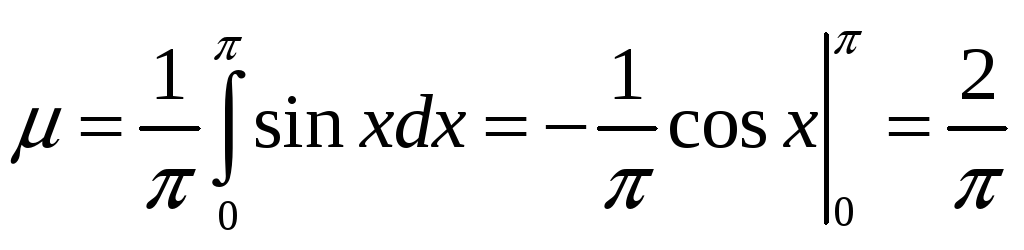 .
.
Формула интегрирования по частям.
Теорема.
Если функции
![]() и
и
![]() непрерывно дифференцируемы на отрезке
непрерывно дифференцируемы на отрезке
![]() ,
то справедливо соотношение
,
то справедливо соотношение
![]() .
.
Доказательство.
![]() По
правилу дифференцирования производной
произведения имеем
По
правилу дифференцирования производной
произведения имеем
![]() .
.
По
условию все функции в этом равенстве
непрерывны, а, значит, и интегрируемы
на отрезке
![]() .
Используя линейность интеграла и формулу
Ньютона-Лейбница, получаем
.
Используя линейность интеграла и формулу
Ньютона-Лейбница, получаем
![]() .
.![]()
Пример
3.
 .
.
Замена переменной в определенном интеграле.
Теорема.
Если
![]() - непрерывно дифференцируемое отображение
отрезка
- непрерывно дифференцируемое отображение
отрезка
![]() в отрезок
в отрезок
![]() такое, что
такое, что
![]() ,
то при любой непрерывной на
,
то при любой непрерывной на
![]() функции
функции
![]() справедливо равенство
справедливо равенство
 .
.
Доказательство.
![]() Пусть
Пусть
![]() - первообразная функции
- первообразная функции
![]() ,
тогда по теореме о дифференцировании
сложной функции, функция
,
тогда по теореме о дифференцировании
сложной функции, функция
![]() будет первообразной для функции
будет первообразной для функции
![]() .
По формуле Ньютона-Лейбница получаем
.
По формуле Ньютона-Лейбница получаем
 .
.![]()
Пример
4. ![]()

 .
.
