Вопрос №3. Электрический диполь. Дипольный момент. Поле диполя.

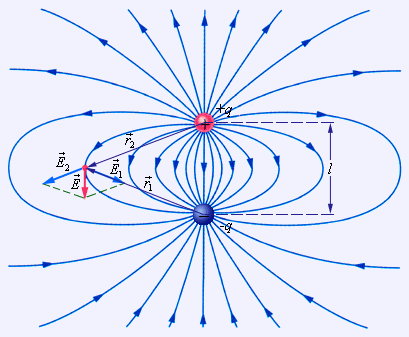
В качестве примера применения принципа суперпозиции полей на рис. 1.2.3. изображена картина силовых линий поля электрического диполя – системы из двух одинаковых по модулю зарядов разного знака q и –q, расположенных на некотором расстоянии l.

Рисунок 1.2.3. Силовые линии поля электрического диполя

Важной характеристикой электрического диполя является так называемый дипольный момент p:

где l – вектор, направленный от отрицательного заряда к положительному, модуль   Диполь может служить электрической моделью многих молекул.

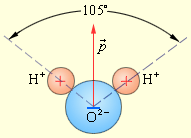
Электрическим дипольным моментом обладает, например, нейтральная молекула воды (H₂O), так как центры двух атомов водорода располагаются не на одной прямой с центром атома кислорода, а под углом 105° (рис. 1.2.4). Дипольный момент молекулы воды p = 6,2·10^–30 Кл · м.

Рисунок 1.2.4.

Используя принцип суперпозиции, напряженность Е поля диполя в любой точке поля    где Е₊ и Е_-– — напряженности полей, которые создаются соответственно положительным и отрицательным зарядами. Применяя эту формулу, найдем напряженность поля в произвольной точке на продолжении оси диполя и на перпендикуляре к середине его оси. 

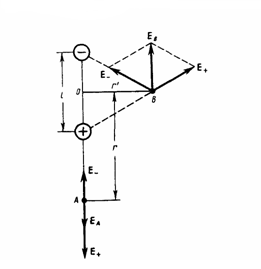1. Напряженность поля на продолжении оси диполя в точке А (рис. 2). Из рисунка видно, что напряженность поля диполя в точке А направлена по оси диполя и по модулю будет равна    Обозначив расстояние от точки А до середины оси диполя как r, используя формулу напряженности поля точечного заряда для вакуума, запишем    Согласно определению диполя, l/2<<r, поэтому    2. Напряженность поля на перпендикуляре, проведенном к оси из его середины, в точке В (рис. 2). Точка В находится на равном расстоянии от зарядов, поэтому   (4)  где r' — расстояние от точки В до середины плеча диполя. Из подобия равнобедренных треугольников, которые опираются на плечо диполя и вектор Е_B, получим    откуда   (5)  В выражение (5) подставим (4), получим 

Вопрос №4. Теорема Гаусса для электростатики (в интегральной и дифференциальной форме).

Поток вектора напряженности электрического поля. Пусть небольшую площадку ΔS  пересекают силовые линии электрического поля, направление которых составляет с нормалью n к этой площадке угол α.

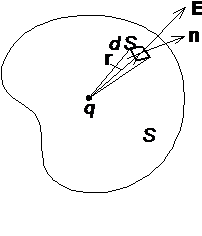
Полагая, что вектор напряженности Е не меняется в пределах площадки ΔS, определим поток вектора напряженности через площадку ΔS как

ΔФ_E = E ΔS cos α.       (1)

Поскольку густота силовых линий равна численному значению напряжённости E, то количество силовых линий, пересекающих площадку ΔS, будет численно равно значению потока ΔФ_E через поверхность ΔS. Для элементарной площадки dS выражение (1) принимает вид

dФ_E = E dS

Через всю площадку S поток вектора напряженности вычисляется как интеграл по поверхности

Теорема Гаусса. Рассмотрим точечный положительный электрический заряд q, находящийся внутри произвольной замкнутой поверхности S. Поток вектора индукции через элемент поверхности dS равен    (2)

Если электрическое поле создаётся системой точечных зарядов q₁, q₂,…, q_n, которая охватывается замкнутой поверхностью S, то, в соответствии с принципом суперпозиции, поток вектора индукции через эту поверхность определяется как сумма потоков, создаваемых каждым из зарядов. Поток вектора электрической индукции через замкнутую поверхность произвольной формы равен алгебраической сумме зарядов, охваченных этой поверхностью:

     (3)

Если в пространстве, ограниченном замкнутой поверхностью S, электрический заряд распределен непрерывно, то следует считать, что каждый элементарный объём dV имеет заряд  . В этом случае в правой части выражения (3) алгебраическое суммирование зарядов заменяется интегрированием по объёму, заключённому внутри замкнутой поверхности S:

    (4)

Выражение (4) является наиболее общей формулировкой теоремы Гаусса: поток вектора электрической индукции через замкнутую поверхность произвольной формы равен суммарному заряду в объеме, охваченном этой поверхностью, и не зависит от зарядов, расположенных вне рассматриваемой поверхности.

Из теоремы Гаусса следует важное свойство электрического поля: силовые линии начинаются или заканчиваются только на электрических зарядах или уходят в бесконечность.

Дифференциальная форма теоремы Гаусса. Отметим, что интегральная форма теоремы Гаусса характеризует соотношения между источниками электрического поля (зарядами) и характеристиками электрического поля (напряженностью или индукцией) в объеме V произвольной, но достаточной для формирования интегральных соотношений, величины. Производя деление объема V на малые объемы V_i , получим выражение

справедливое как в целом, так и для каждого слагаемого. Преобразуем полученное выражение следующим образом:

     (5)

и рассмотрим предел, к которому стремится выражение в правой части равенства, заключенное в фигурных скобках, при неограниченном делении объема V. В математике этот предел называют дивергенцией вектора (в данном случае вектора электрической индукции D):

Дивергенция вектора D в декартовых координатах:

Таким образом выражение (5) преобразуется к виду:

 _.

Учитывая, что при неограниченном делении сумма в левой части последнего выражения переходит в объемный интеграл, получим

Полученное соотношение должно выполняться для любого произвольно выбранного объема V. Это возможно лишь в том случае, если значения подынтегральных функций в каждой точке пространства одинаковы. Следовательно, дивергенция вектора D связана с плотностью заряда в той же точке равенством

или для вектора напряженности электростатического поля

.

Эти равенства выражают теорему Гаусса в дифференциальной форме.

Отметим, что в процессе перехода к дифференциальной форме теоремы Гаусса получается соотношение, которое имеет общий характер:

_.

Выражение называется формулой Гаусса - Остроградского и связывает интеграл по объему от дивергенции вектора с потоком этого вектора сквозь замкнутую поверхность, ограничивающую объем.

Вопрос №5.

Потенциальный характер электростатического поля. Интегральная и дифференциальная формулировки критерия потенциальности. Скалярный потенциал, разность потенциалов. Градиент потенциала. Уравнения Пуассона и Лапласа.

Поле сил называется потенциальным, если работа при перемещении заряда в этом поле зависит лишь от начальной и конечной точек пути и не зависит от траектории (а также А=0 при перемещении по замкнутому контуру).

Кулоновская сила убывает обратно пропорционально квадрату расстояний (как и сила тяжести точечной массы, которая является потенциальной), следовательно, она является потенциальной.

Из потенциальности поля точечного заряда => потенциальность произвольного электрического поля (по суперпозиции).

Вопрос №6.

Постоянное электрическое поле при наличии проводников. Электрическая емкость уединенного проводника.

Вопрос №7.

Силы в электростатическом поле, действующие на заряд, на диполь.

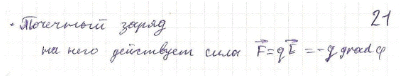
Вопрос №8.

Энергия электростатического поля. Энергия заряженного конденсатора. Энергия диполя во внешнем поле.

Вопрос №9.

Постоянное электрическое поле при наличии диэлектрика. Поляризованность диэлектрика. Диэлектрическая восприимчивость и диэлектрическая проницаемость.

Вопрос №10.

Объемные и поверхностные поляризационные заряды в диэлектрике. Вектор электрического смещения. Теорема Гаусса при наличии диэлектрика. Граничные условия для вектора напряженности и смещения.

Вопрос №11.

Молекулярная картина поляризации диэлектриков. Электронная, ионная и дипольная поляризация. Формула Клазиуса-Мосотти. Формула Дебая-Ланжевена.

Вопрос №12.

Сегнетоэлектрики и пьезоэлектрики. Прямой и обратный пьезоэлектрический эффект.

Вопрос №13.

Условия существования постоянного электрического тока. Сторонняя ЭДС.

Для существования постоянного электрического тока необходимо наличие свободных заряженных частиц и наличие источника тока. в котором осуществляется преобразование какого-либо вида энергии в энергию электрического поля.

Источник тока - устройство, в котором осуществляется преобразование какого-либо вида энергии в энергию электрического поля. В источнике тока на заряженные частицы в замкнутой цепи действуют сторонние силы. Причины возникновения сторонних сил в различных источниках тока различны. Например в аккумуляторах и гальванических элементах сторонние силы возникают благодаря протеканию химических реакций, в генераторах электростанций они возникают  при движении проводника в магнитном поле, в фотоэлементах - при действия света на электроны в металлах и полупроводниках.

Электродвижущей силой источника тока называют отношение работы сторонних сил к величине положительного заряда, переносимого от отрицательного полюса источника тока к положительному.

Таким образом, ЭДС определяется работой, совершаемой сторонними силами при перемещении единичного положительного заряда. Электродвижущая сила, как и разность потенциалов, измеряется в вольтах (В).

При перемещении единичного положительного заряда по замкнутой цепи постоянного тока работа сторонних сил равна сумме ЭДС, действующих в этой цепи, а работа электростатического поля равна нулю.

Причиной электродвижущей силы может стать изменение магнитного поля в окружающем пространстве. Это явление называется электромагнитной индукцией. Величина ЭДС индукции в контуре определяется выражением

где Φ — поток магнитного поля через замкнутую поверхность S, ограниченную контуром. Знак «−» перед выражением показывает, что индукционный ток, созданный ЭДС индукции, препятствует изменению магнитного потока в контуре.