МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
ДНІПРОДЗЕРЖИНСЬКИЙ ДЕРЖАВНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ
МЕТОДИЧНІ ВКАЗІВКИ
до самостійної роботи з дисципліни
«Математичний аналіз»
(змістовий модуль 3)
для студентів, що навчаються за напрямом
6.040301 “Прикладна математика”
ЗАТВЕРДЖЕНО:
Редакційно-видавничою секцією
науково-методичної ради ДДТУ
“ _____ ” _____ 2012 р. протокол №
Дніпродзержинськ
2012
Розповсюдження і тиражування без офіційного дозволу Дніпродзержинського державного технічного університету заборонено.
Методичні вказівки до самостійної роботи з дисципліни «Математичний аналіз» для студентів, що навчаються за напрямом 6.040301 “Прикладна математика” (змістовий модуль 3) / Укладач С.В.Тимченко – Дніпродзержинськ, ДДТУ, 2012. - 40 с.
Укладач: С.В.Тимченко, ст. викладач
Відповідальний за випуск: С.Є.Самохвалов,
проф., доктор техн. наук
Рецензент: Л.О.Черномурова, к.ф.-м.наук, доцент
Затверджено на засіданні кафедри ПМ
протокол № 16 від 29 травня 2012 р.
Коротка анотація до видання. У методичних вказівках до самостійної роботи студентів з дисципліни “Математичний аналіз” (змістовий модуль 3) надано варіанти індивідуальних завдань для модульного контролю. Наведено зразок виконання індивідуального завдання.
ЗМІСТ
Вступ . . . . . . . . . . . . . . . . . . . . . . . . . . 4 |
Варіант 1 . . . . . . . . . . . . . . . . . . . . . . . . . . 5 |
Варіант 2 . . . . . . . . . . . . . . . . . . . . . . . . . . 6 |
Варіант 3 . . . . . . . . . . . . . . . . . . . . . . . . . . 7 |
Варіант 4 . . . . . . . . . . . . . . . . . . . . . . . . . . 9 |
Варіант 5 . . . . . . . . . . . . . . . . . . . . . . . . . . 10 |
Варіант 6 . . . . . . . . . . . . . . . . . . . . . . . . . . 11 |
Варіант 7 . . . . . . . . . . . . . . . . . . . . . . . . . . 13 |
Варіант 8 . . . . . . . . . . . . . . . . . . . . . . . . . . 14 |
Варіант 9 . . . . . . . . . . . . . . . . . . . . . . . . . . 15 |
Варіант 10 . . . . . . . . . . . . . . . . . . . . . . . . . 17 |
Варіант 11 . . . . . . . . . . . . . . . . . . . . . . . . . 18 |
Варіант 12 . . . . . . . . . . . . . . . . . . . . . . . . . 19 |
Варіант 13 . . . . . . . . . . . . . . . . . . . . . . . . . 21 |
Варіант 14 . . . . . . . . . . . . . . . . . . . . . . . . . 22 |
Варіант 15 . . . . . . . . . . . . . . . . . . . . . . . . . 23 |
Варіант 16 . . . . . . . . . . . . . . . . . . . . . . . . . 25 |
Варіант 17 . . . . . . . . . . . . . . . . . . . . . . . . . 26 |
Варіант 18 . . . . . . . . . . . . . . . . . . . . . . . . . 27 |
Варіант 19 . . . . . . . . . . . . . . . . . . . . . . . . . 29 |
Варіант 20 . . . . . . . . . . . . . . . . . . . . . . . . . 30 |
Зразок виконання індивідуального завдання . . . . . . 31 |
Перелік літератури . . . . . . . . . . . . . . . . . . . . 40 |
ВСТУП
Важливим елементом засвоєння математики й оволодіння її методами є самостійна робота студентів. Ця робота є неперервною складовою виконання поточних домашніх завдань і циклічної роботи з виконання індивідуальних модульних завдань. Результативність самостійної роботи студентів забезпечується ефективною системою контролю, яка включає опитування студентів за змістом лекції, перевірку виконання поточних домашніх завдань, розв’язування задач біля дошки, захист індивідуальних модульних робіт.
Метою індивідуальних домашніх завдань є перевірка результативності самостійної роботи з даного модуля.
Студент повинен самостійно розв’язати індивідуальні домашні завдання свого варіанта, який відповідає номеру студента у списку навчальної групи.
Розв’язання завдань із поясненнями слід подати у зошиті, на обкладинці якого необхідно написати назву дисципліни та модуля; прізвище студента, його ім’я і по батькові; курс, номер групи; номер варіанта. Кожне завдання необхідно позначати його номером за методичними вказівками. Умову завдання треба переписати повністю.
Якщо після перевірки роботи викладачем зроблені зауваження, студент повинен розв’язати наново неправильно виконані завдання у тому самому зошиті і повторно подати його на перевірку. Після позитивної оцінки викладача робота підлягає захисту.
ВАРІАНТ 1
Завдання 1. Знайти невизначені інтеграли:
а)
б)
Завдання 2. Проінтегрувати раціональні дробі:
а)
б)
Завдання 3. Обчислити інтеграли від тригонометричних функцій
а)
;
б)
;
в)
.
Завдання 4. Обчислити інтеграл від ірраціональної функції:
а)
;
б)
;
в)
Завдання 5. Обчислити визначені інтеграли:
а)
б)
в)
Завдання 6. Обчислити площу плоскої фігури:
а)
б)
в)
Завдання 7. Обчислити довжину дуги кривої:
а)
б)
в)
ВАРІАНТ 2
Завдання 1. Знайти невизначені інтеграли:
а)
б)
Завдання 2. Проінтегрувати раціональні дробі:
а)
б)
Завдання 3. Обчислити інтеграли від тригонометричних функцій
а)
; б)
; в)
.
Завдання 4. Обчислити інтеграл від ірраціональної функції:
а)
; б)
; в)
Завдання 5. Обчислити визначені інтеграли:
а)
б)
в)
Завдання 6. Обчислити площу плоскої фігури:
а)
б)
в)
Завдання 7. Обчислити довжину дуги кривої:
а)
б)
в)
ВАРІАНТ 3
Завдання 1. Знайти невизначені інтеграли:
а)
б)
Завдання 2. Проінтегрувати раціональні дробі:
а)
б)
Завдання 3. Обчислити інтеграли від тригонометричних функцій
а)
; б)
; в)
.
Завдання 4. Обчислити інтеграл від ірраціональної функції:
а)
; б)
; в)
Завдання 5. Обчислити визначені інтеграли:
а)
б)
в)
Завдання 6. Обчислити площу плоскої фігури:
а)
б)
в)
Завдання 7. Обчислити довжину дуги кривої:
а)
б)
в)
ВАРІАНТ 4
Завдання 1. Знайти невизначені інтеграли:
а)
б)
Завдання 2. Проінтегрувати раціональні дробі:
а)
б)
Завдання 3. Обчислити інтеграли від тригонометричних функцій
а)
; б)
; в)
.
Завдання 4. Обчислити інтеграл від ірраціональної функції:
а)
; б)
; в)
Завдання 5. Обчислити визначені інтеграли:
а)
б)
в)
Завдання 6. Обчислити площу плоскої фігури:
а)
б)
в)
Завдання 7. Обчислити довжину дуги кривої:
а)
б)
в)
ВАРІАНТ 5
Завдання 1. Знайти невизначені інтеграли:
а)
б)
Завдання 2. Проінтегрувати раціональні дробі:
а)
б)
Завдання 3. Обчислити інтеграли від тригонометричних функцій
а)
; б)
; в)
.
Завдання 4. Обчислити інтеграл від ірраціональної функції:
а)
;
б)
;
в)
Завдання 5. Обчислити визначені інтеграли:
а)
б)
в)
Завдання 6. Обчислити площу плоскої фігури:
а)
б)
в)
Завдання 7. Обчислити довжину дуги кривої:
а)
б)
в)
ВАРІАНТ 6
Завдання 1. Знайти невизначені інтеграли:
а)
б)
Завдання 2. Проінтегрувати раціональні дробі:
а)
б)
Завдання 3. Обчислити інтеграли від тригонометричних функцій
а)
; б)
; в)
.
Завдання 4. Обчислити інтеграл від ірраціональної функції:
а)
;
б)
;
в)
Завдання 5. Обчислити визначені інтеграли:
а)
б)
в)
Завдання 6. Обчислити площу плоскої фігури:
а)
б)
в)
Завдання 7. Обчислити довжину дуги кривої:
а)
б)
в)
ВАРІАНТ 7
Завдання 1. Знайти невизначені інтеграли:
а)
б)
Завдання 2. Проінтегрувати раціональні дробі:
а)
б)
Завдання 3. Обчислити інтеграли від тригонометричних функцій
а)
;
б)
; в)
.
Завдання 4. Обчислити інтеграл від ірраціональної функції:
а)
; б)
;
в)
Завдання 5. Обчислити визначені інтеграли:
а)
б)
в)
Завдання 6. Обчислити площу плоскої фігури:
а)
б)
в)
Завдання 7. Обчислити довжину дуги кривої:
а)
б)
в)
ВАРІАНТ 8
Завдання 1. Знайти невизначені інтеграли:
а)
б)
Завдання 2. Проінтегрувати раціональні дробі:
а)
б)
Завдання 3. Обчислити інтеграли від тригонометричних функцій
а)
; б)
;
в)
.
Завдання 4. Обчислити інтеграл від ірраціональної функції:
а)
;
б)
;
в)
Завдання 5. Обчислити визначені інтеграли:
а)
б)
в)
.
Завдання 6. Обчислити площу плоскої фігури:
а)
б)
в)
.
Завдання 7. Обчислити довжину дуги кривої:
а)
б)
в)
ВАРІАНТ 9
Завдання 1. Знайти невизначені інтеграли:
а)
б)
Завдання 2. Проінтегрувати раціональні дробі:
а)
б)
Завдання 3. Обчислити інтеграли від тригонометричних функцій
а)
; б)
; в)
.
Завдання 4. Обчислити інтеграл від ірраціональної функції:
а)
;
б)
;
в)
Завдання 5. Обчислити визначені інтеграли:
а)
б)
в)
Завдання 6. Обчислити площу плоскої фігури:
а)
б)
в)
Завдання 7. Обчислити довжину дуги кривої:
а)
б)
в)
ВАРІАНТ 10
Завдання 1. Знайти невизначені інтеграли:
а)
б)
Завдання 2. Проінтегрувати раціональні дробі:
а)
б)
Завдання 3. Обчислити інтеграли від тригонометричних функцій
а)
;
б)
;
в)
.
Завдання 4. Обчислити інтеграл від ірраціональної функції:
а)
;
б)
;
в)
Завдання 5. Обчислити визначені інтеграли:
а)
б)
в)
Завдання 6. Обчислити площу плоскої фігури:
а)
б)
в)
Завдання 7. Обчислити довжину дуги кривої:
а)
б)
в)
ВАРІАНТ 11
Завдання 1. Знайти невизначені інтеграли:
а)
б)
Завдання 2. Проінтегрувати раціональні дробі:
а)
б)
Завдання 3. Обчислити інтеграли від тригонометричних функцій
а)
; б)
;
в)
.
Завдання 4. Обчислити інтеграл від ірраціональної функції:
а)
; б)
;
в)
Завдання 5. Обчислити визначені інтеграли:
а)
б)
в)
Завдання 6. Обчислити площу плоскої фігури:
а)
б)
в)
Завдання 7. Обчислити довжину дуги кривої:
а)
б)
в)
ВАРІАНТ 12
Завдання 1. Знайти невизначені інтеграли:
а)
б)
Завдання 2. Проінтегрувати раціональні дробі:
а)
б)
Завдання 3. Обчислити інтеграли від тригонометричних функцій
а)
; б)
; в)
.
Завдання 4. Обчислити інтеграл від ірраціональної функції:
а)
; б)
;
в)
Завдання 5. Обчислити визначені інтеграли:
а)
б)
в)
Завдання 6. Обчислити площу плоскої фігури:
а)
б)
в)
Завдання 7. Обчислити довжину дуги кривої:
а)
б)
в)
ВАРІАНТ 13
Завдання 1. Знайти невизначені інтеграли:
а)
б)
Завдання 2. Проінтегрувати раціональні дробі:
а)
б)
Завдання 3. Обчислити інтеграли від тригонометричних функцій
а)
; б)
; в)
.
Завдання 4. Обчислити інтеграл від ірраціональної функції:
а)
;
б)
;
в)
Завдання 5. Обчислити визначені інтеграли:
а)
б)
в)
Завдання 6. Обчислити площу плоскої фігури:
а)
б)
в)
Завдання 7. Обчислити довжину дуги кривої:
а)
б)
в)
ВАРІАНТ 14
Завдання 1. Знайти невизначені інтеграли:
а)
б)
Завдання 2. Проінтегрувати раціональні дробі:
а)
б)
Завдання 3. Обчислити інтеграли від тригонометричних функцій
а)
; б)
; в)
.
Завдання 4. Обчислити інтеграл від ірраціональної функції:
а)
; б)
; в)
Завдання 5. Обчислити визначені інтеграли:
а)
б)
в)
Завдання 6. Обчислити площу плоскої фігури:
а)
б)
в)
Завдання 7. Обчислити довжину дуги кривої:
а)
б)
в)
ВАРІАНТ 15
Завдання 1. Знайти невизначені інтеграли:
а)
б)
Завдання 2. Проінтегрувати раціональні дробі:
а)
б)
Завдання 3. Обчислити інтеграли від тригонометричних функцій
а)
;
б)
;
в)
.
Завдання 4. Обчислити інтеграл від ірраціональної функції:
а)
;
б)
;
в)
Завдання 5. Обчислити визначені інтеграли:
а)
б)
в)
Завдання 6. Обчислити площу плоскої фігури:
а)
б)
в)
Завдання 7. Обчислити довжину дуги кривої:
а)
б)
в)
ВАРІАНТ 16
Завдання 1. Знайти невизначені інтеграли:
а)
б)
Завдання 2. Проінтегрувати раціональні дробі:
а)
б)
Завдання 3. Обчислити інтеграли від тригонометричних функцій
а)
;
б)
;
в)
.
Завдання 4. Обчислити інтеграл від ірраціональної функції:
а)
; б)
;
в)
Завдання 5. Обчислити визначені інтеграли:
а)
б)
в)
Завдання 6. Обчислити площу плоскої фігури:
а)
б)
в)
Завдання 7. Обчислити довжину дуги кривої:
а)
б)
в)
ВАРІАНТ 17
Завдання 1. Знайти невизначені інтеграли:
а)
б)
Завдання 2. Проінтегрувати раціональні дробі:
а)
б)
Завдання 3. Обчислити інтеграли від тригонометричних функцій
а)
; б)
; в)
.
Завдання 4. Обчислити інтеграл від ірраціональної функції:
а)
;
б)
; в)
Завдання 5. Обчислити визначені інтеграли:
а)
б)
в)
Завдання 6. Обчислити площу плоскої фігури:
а)
б)
в)
Завдання 7. Обчислити довжину дуги кривої:
а)
б)
в)
ВАРІАНТ 18
Завдання 1. Знайти невизначені інтеграли:
а)
б)
Завдання 2. Проінтегрувати раціональні дробі:
а)
б)
Завдання 3. Обчислити інтеграли від тригонометричних функцій
а)
;
б)
; в)
.
Завдання 4. Обчислити інтеграл від ірраціональної функції:
а)
;
б)
;
в)
Завдання 5. Обчислити визначені інтеграли:
а)
;
б)
в)
.
Завдання 6. Обчислити площу плоскої фігури:
а)
б)
в)
Завдання 7. Обчислити довжину дуги кривої:
а)
б)
в)
ВАРІАНТ 19
Завдання 1. Знайти невизначені інтеграли:
а)
б)
Завдання 2. Проінтегрувати раціональні дробі:
а)
б)
Завдання 3. Обчислити інтеграли від тригонометричних функцій
а)
; б)
; в)
.
Завдання 4. Обчислити інтеграл від ірраціональної функції:
а)
; б)
; в)
Завдання 5. Обчислити визначені інтеграли:
а)
б)
в)
Завдання 6. Обчислити площу плоскої фігури:
а)
б)
в)
Завдання 7. Обчислити довжину дуги кривої:
а)
б)
в)
ВАРІАНТ 20
Завдання 1. Знайти невизначені інтеграли:
а)
б)
Завдання 2. Проінтегрувати раціональні дробі:
а)
б)
Завдання 3. Обчислити інтеграли від тригонометричних функцій:
а)
; б)
; в)
.
Завдання 4. Обчислити інтеграл від ірраціональної функції:
а)
; б)
; в)
Завдання 5. Обчислити визначені інтеграли:
а)
б)
в)
Завдання 6. Обчислити площу плоскої фігури:
а)
б)
в)
Завдання 7. Обчислити довжину дуги кривої:
а)
б)
в)
Зразок виконання індивідуального завдання
Завдання 1. Обчислити невизначені інтеграли:
а)
б)
Розв’язування.
а) Розпишемо заданий інтеграл у вигляді суми двох:
.
Розглянемо окремо кожен інтеграл.
=
,
=
.
Тоді
.
б) Застосовуємо формулу інтегрування частинами:
=
.
Завдання 2. Проінтегрувати раціональні дробі:
а)
б)
Розв'язання.
а) Під інтегралом розташована правильний раціональний дріб:
.
Застосуємо метод невизначених координат, отримаємо
.
Звідси
|
|
|
|
|
|
Тоді
.
б) Під інтегралом розташована правильний раціональний дріб:
.
Застосуємо метод невизначених коефіцієнтів, отримаємо
,
.
Звідси
|
|
|
|
|
|
|
|
,
,
,
.
Розв'язком
отриманої системи є
,
,
,
.
Тоді
.
Завдання 3. Обчислити інтеграли від тригонометричних функцій:
а)
;
б)
;
в)
.
Розв'язання.
а)
Для знаходження інтегралу перетворимо
підінтегральний вираз за формулою
.
Маємо
.
б)
У чисельнику відокремлюємо один
та вносимо його під знак диференціала:
.
в)
Для спрощення підінтегрального виразу
застосовуємо універсальну тригонометричну
підстановку, а саме
,
тоді
,
,
.
Маємо
.
Завдання 4. Обчислити інтеграл від ірраціональної функції:
а)
; б)
,
в)
Розв'язання.
а)
Покладемо
,
тоді
і
.
Тоді
.
б)
Маємо
,
,
тому
.
Застосовуємо підстановку
,
тоді
,
і, отже,
Повертаємося
до старої змінної. Оскільки
,
то
.
в) Перепишемо даний інтеграл наступним чином:
.
До
даного інтегралу застосуємо правило
інтегрування диференціальних біномів.
Маємо
,
,
,
вираз
є
цілим числом, тому введемо підстановку
.
Звідси
,
,
тоді
.
Завдання 5. Обчислити визначні інтеграли:
а)
б) 
в)
Розв'язання.
а) Для обчислення інтегралу застосуємо формулу інтегрування частинами:
.
б) У підкореневому виразі виділимо повний квадрат:
,
тоді
.
в)
Для
спрощення підінтегрального виразу
застосовуємо універсальну тригонометричну
підстановку, а саме
,
тоді
,
.
Змінимо границі інтегрування: якщо
,
то
,
якщо
,
то
.
Таким чином,
.
Завдання
6.
а) Обчислити площу плоскої фігури, що
обмежена лініями:
,
.
Розв'язання.
Знайдемо точки
перетину параболи та прямої, для чого
розв’яжемо систему рівнянь:
.
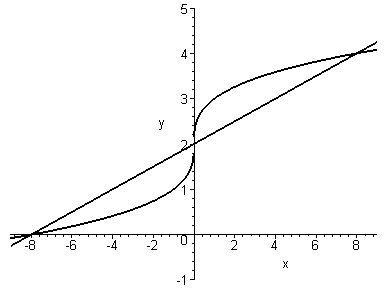
Рис. 1. |
Маємо
Отже, задані криві перетина-ються в точках А(-8; 0), В(0; 2) і С(8; 4) (рис.1). |
,
,
,
і
,
,
.
Враховуючи, що фігура симетрична, отримуємо
(кв.од.).
Завдання
6.
б) Обчислити площу плоскої фігури, що
обмежена лінією:
та прямою
.
Розв'язання.
Крива, що обмежує
область, задана у параметричному вигляді.
Отже, площа криволінійної трапеції, що
обмежена цією кривою, виражається
формулою
.
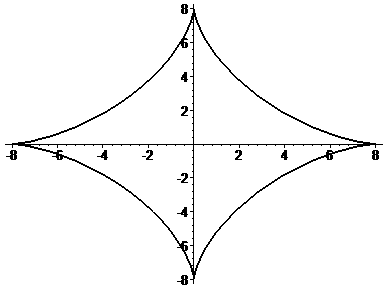
Рис. 2. |
Знайдемо
точки перетину прямої та лінії
Оскільки
область симетрична, то
|
:
(рис.2).
.
Знайдемо
похідну функції
.
Враховуючи, що при зміні параметру від
,
змінна
,
отримуємо:
(кв.од.).
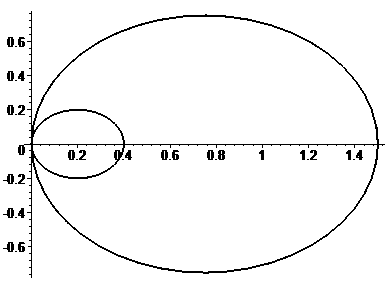
в)
Обчислити площу плоскої фігури, що
обмежена лініями
,
(рис. 3).
Розв'язання.
Рис. 3. |
Площа криволінійного сектора, обмеженого кривими, заданими в полярній системі координат, знаходимо за формулою
Половині
шуканої площі відповідає зміна кута
|
.
від 0 до
,
тому
(кв.од.).
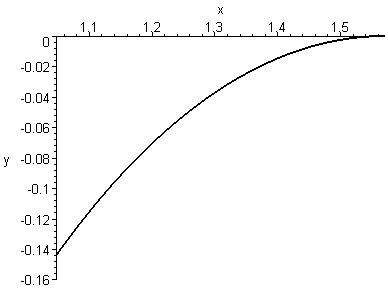
Завдання
7.
а) Обчислити довжину дуги кривої
,
(рис. 4) .
Розв'язання.
Рис. 4. |
Крива
на відрізку
Шляхом диференціювання рівняння кривої знаходимо |
є гладкою, отже довжина відповідної
дуги знаходиться за формулою
.
,
тому
.
Отже,
(лін.од.).
б)
Обчислити довжину дуги кривої
,
від
до
.