Средняя квадратическая

Используется в тех случаях, когда при замене индивидуальных значений признака на среднюю величину необходимо сохранить неизменной сумму квадратов исходных величин.

Главная сфера её использования – измерение степени колеблемости индивидуальных значений признака относительно средней арифметической (среднее квадратическое отклонение). Кроме этого, средняя квадратическая применяется в тех случаях, когда необходимо вычислить средний величину признака, выраженного в квадратных или кубических единицах измерения (при вычислении средней величины квадратных участков, средних диаметров труб, стволов и т. д.).

Средняя квадратическая рассчитывается в двух формах:

- как простая

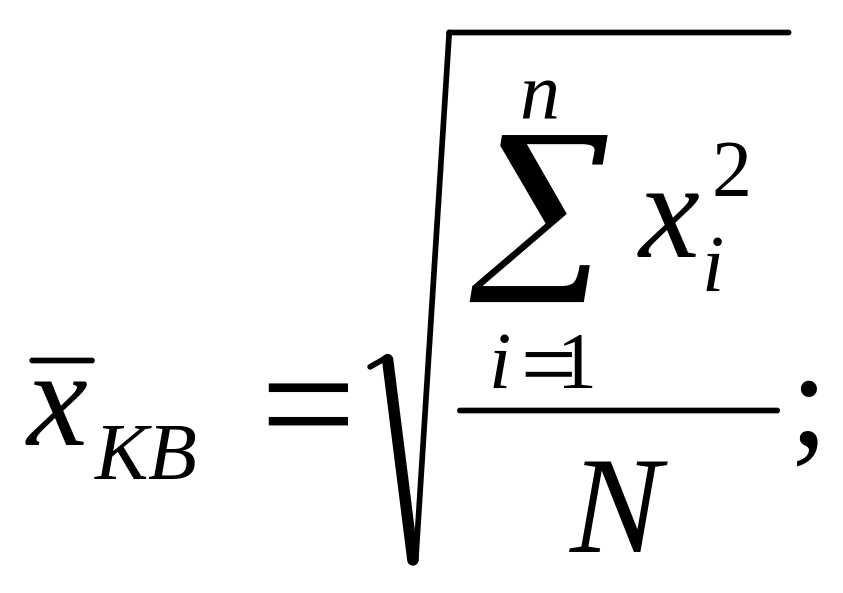
как взвешенная

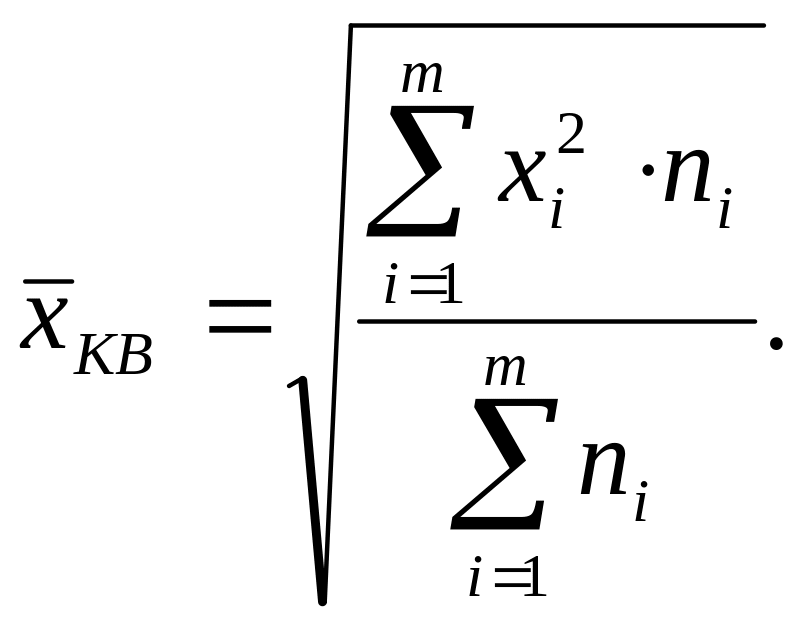
Особый вид средних показателей – структурные средние. Они используются при изучении внутреннего строения рядов распределения значений признака. К ним относятся мода и медиана.

Мода и медиана характеризуют значение признака у статистической единицы, занимающей определенное положение в вариационном ряду.

Мода (Mo) - наиболее часто встречаемое значение признак в совокупности. Мода широко используется в статистической практике при изучении покупательского спроса, регистрации цен и др.

Медиана (Me) - значение признака у статистической единицы, стоящей в середине ранжированного ряда и делящей совокупность на две равные по численности части.

Для дискретных вариационных рядов Mo и Me выбираются в соответствии с определениями: мода - как значение признака с наибольшей частотой\ n_i ; положение медианы при нечетном объеме совокупности определяется ее номером , где N – объем статистической совокупности. При четном объеме ряда медиана равна средней из двух вариантов, находящихся в середине ряда.

Мода определяется следующим образом:

• По максимальному значению частоты определяется интервал, в котором находится значение моды. Он называется модальным.

• Внутри модального интервала значение моды вычисляется по формуле:

где - нижняя граница модального интервала;

a_Мо - ширина модального интервала;

n_Мо , n_Мо-1, n_Мо+1 - соответственно частоты модального, предмодального (предшествующего модальному) и постмодального (следующего за модальным) интервалов.

Для расчета медианы в интервальных рядах используется следующий подход:

• По накопленным частотам находится медианный интервал.

Медианным называется интервал, содержащий центральную единицу.

• Внутри медианного интервала значение Me определяется по формуле:

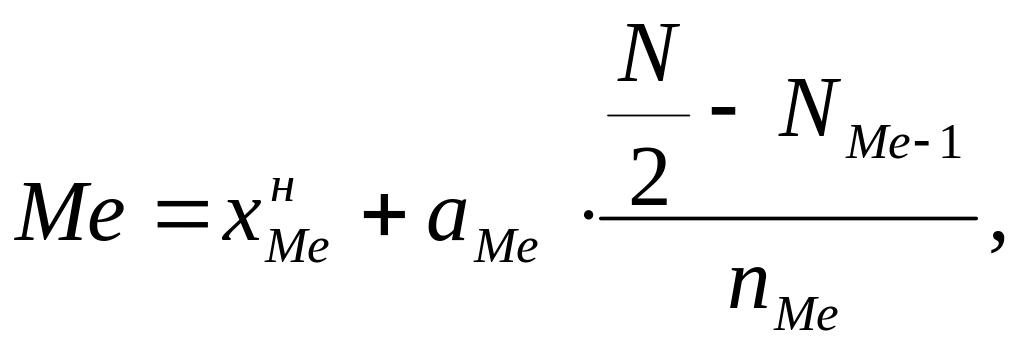
где - нижняя граница медианного интервала;

a_Ме -ширина медианного интервала;

N – объем статистической совокупности;

N _Ме-1- накопленная частота предмедианного интервала;

n _Ме - частота медианного интервала.

Упражнения и задачи

Задача 3.1

По плану завод должен выпустить в отчетном периоде товарной продукции на 14 млн. д.е. при средней численности работающих 380 чел. Фактически выпуск товарной продукции составил в этом периоде 13,4 млн. д.е. при средней численности работающих 420 чел. Определите: а) относительную величину выполнения плана по выпуску товарной продукции; б) относительную величину выполнения плана по численности работающих; в) показатель изменения фактического выпуска продукции на одного работающего в сравнении с планом.

Задача 3.2.

Имеются следующие данные (табл. 3.1) о производстве однородной продукции за 2003-2008 г.г. предприятиями региона (тыс. т.)

Таблица 3.1 – Объем производства продукции

2003	2004	2005	2006	2007	2008
420	440	466	498	512	540

Определите относительные величины динамики производства продукции цепным и базисным способами, приняв за базу сравнения 2003 год.

Задача 3.3

По данным о численности населения Брянской области (табл.3.2) рассчитать относительные величины (структуры, динамики, координат, интенсивности).

Таблица 3.2 - Численность населения Брянской области

на начало года

Годы	Численность населения, тыс.чел.	в том числе:
		моложе трудоспособного возраста	трудоспособного возраста	старше трудоспособного возраста
2006	1331,4	212,5	810,8	308,1
2007	1317,6	204,5	807,4	305,7

Задача 3.4

Объем реализации платных услуг для населения области за год составил 149,6 млн. д.е., в том числе предоставленных государственными предприятиями на сумму 100,9 млн. д.е., коллективными предприятиями на сумму 48,1 млн. д.е. и частными – 0,6 млн. д.е.

Определите относительные величины структуры и отобразите их в виде секторной диаграммы.

Задача 3.5

На основе следующих данных (табл. 3.3) рассчитать различные виды относительных показателей, характеризующих производство зерна в фермерских хозяйствах.

Таблица 3.3 – Производство зерна в фермерских хозяйствах

Периоды	Фермерское хозяйство 1				Фермерское хозяйство 2
	Посевная площадь, га		Валовой сбор зерна, т		Урожайность зерновых культур, ц/га
	Всего	В том числе зерновых	План	Факт
Базисный	470	240	310	390	26
Отчетный	585	234	400	430	28

Задача 3.6

Имеются данные (табл. 3.4) о распределении городского и сельского населения в регионе по полу (тыс. чел.).

Таблица 3.4 – Данные о численности населения

Группы населения на территории	Всего	В том числе
		Мужчины	Женщины
Общая численность населения	281,3	132,0	149,4
В том числе: Городское	184,8	86,9	97,9
Сельское	96,5	45,1	51,4

Вычислите различные виды относительных показателей.

Задача 3.7

В 2005 г. цех выпустил продукции на 2800 млн р. Плановое задание по выпуску продукции на 2006 г. составляло 2040 млн р., фактически же цех выпустил в этом году продукции на 2996 млн р.

Определите относительные величины планового задания, степени выполнения планового задания и динамики за 2006 г.

Задача 3.8

Среднегодовая численность работающих на промышленном предприятии за отчетный год увеличилась на 5,6%, а удельный вес рабочих в общей численности работающих увеличился на 3,4%.

Определите, как изменилась абсолютная численность рабочих за отчетный период.

Задача 3.9

В результате проверки двух партий сыра перед отправкой его потребителям установлено, что в первой партии сыра высшего сорта было 3942 кг, что составляет 70,4% общего веса сыра этой партии: во второй партии сыра высшего сорта было 6520 кг, что составляет 78,6% общего веса сыра этой партии.

Определите средний процент сыра высшего сорта по первой и второй партиям вместе.

Задача 3.10

По предприятию имеются следующие данные (таблица 3.5) о выпуске продукции за смену:

Таблица 3.5 – Выпуск продукции предприятием А

Количество изделий, выпущенных за смену, шт.	Количество рабочих, чел.
До 6	12
6-8	32
8-10	40
10-12	16
Более 12	6

Вычислите среднее количество изделий за смену.

Задача 3.11

Вычислите среднесуточную выработку угля на шахте по таким данным (табл. 3.6):

Таблица 3.6 – Объем выработки угля в сутки

Число месяца	1	2	3	4	5	6	7	8	9	10
Выработка угля за сутки, тыс.т	4,8	5,0	4,9	5,1	5,3	5,2	5,5	5,7	5,8	6,0

Задача 3.12

Определите среднее количество слов в зарегистрированных за сутки телеграммах и обоснуйте выбор вида средней по следующим данным (табл. 3.7):

Таблица 3.7 – Количество слов в телеграммах

Количество слов	До 4	4-8	8-12	12-16	16-20	20-24
Количество телеграмм	55	92	148	104	67	34

Задача 3.13

Для группы КСП есть данные (табл. 3.8) о среднем надое молока с коровы за год и валовом производстве молока:

Таблица 3.8 - Средний надой молока с коровы за год и валовое производство молока

№ КСП	Средний надой с коровы за год, кг	Валовой надой молока, ц
1	3800	30780
2	3520	33440
3	4500	34200
4	3260	27710
5	3850	25410
6	4100	38540
7	3270	26160
Всего	х	216240

Необходимо вычислить средний годовой надой с коровы для группы КСП.

Задача 3.14

На изготовление одной детали первый фрезеровщик потратил 12 мин., а второй – 15 мин. Определите среднее время изготовления одной детали в течение 8-часового рабочего дня и обоснуйте выбор средней.

Задача 3.15

Имеются данные (табл. 3.9) о посевной площади, урожайности и валовом сборе зерновых культур в двух районах области.

Таблица 3.9 – Исходные данные

Номер совхоза	Первый район		Второй район
	Валовой сбор (ц)	Урожайность (ц/га)	Урожайность (ц/га)	Посевная площадь (га)
1	5300	24	25	310
2	6500	27	28	340
3	6300	32	31	300

Определите среднюю урожайность зерновых в каждом из районов области. Сравните полученные данные по районам. Укажите виды рассчитанных средних величин.

Задача 3.16

Вычислите средние значения показателей по трем группам вузов (табл. 3.10), вместе взятым в отдельном регионе.

Таблица 3.10 – Исходные данные

Группы вузов	Общее число преподавателей	Число преподавателей в среднем в одном вузе	Кандидаты и доктора наук, %	Средний стаж работы преподавателей, лет
Технические	4200	350	74	12
Педагогические	1200	200	78	8
Медицинские	2100	300	89	15

Укажите, какие виды средних величин использовали для расчета всех перечисленных в таблице показателей.

Задача 3.17.

Имеются данные о численности населения в регионе (тыс. чел.), по сравнению на:

1 января – 224,8;	1 июля – 415,8;
1 февраля – 225,0;	1 августа – 452,7;
1 марта – 225,4;	1 сентября – 364,2;
1 апреля – 225,7;	1 октября – 297,1;
1 мая – 325,9;	1 ноября – 228,6;
1 июня – 412,0;	1 декабря – 229,0;
1 января следующего года – 228,0.

Вычислите среднегодовую численность населения в регионе.

Задача 3.18

Имеются данные (табл. 3.11) о динамике объема продукции в сопоставимых ценах в регионе.

Таблица 3.11 – Данные об объеме продукции в регионе (в сопоставимых ценах)

Год	2003	2004	2005	2006	2007	2008
Млн. руб.	600	650	630	700	750	800

Рассчитайте среднегодовой темп роста объема продукции в регионе.

Задача 3.19

Имеются условные данные об урожайности картофеля в хозяйствах (табл. 3.12). Определите среднюю урожайность картофеля в базисном и отчетном периоде различными способами.

Таблица 3.12 - Урожайность картофеля

Хозяйство	Базисный период			Отчетный период
	Урожайность картофеля (x). ц/га	Посевная площадь (f), га	Доля посевной площади (df), га	Урожайность картофеля (х), ц/га	Валовой сбор картофеля (М), ц	Посевная площадь картофеля , га
Первое	180	300	0,30	190	57000	300
Второе	200	200	0,20	210	42000	200
Третье	250	500	0,50	260	130000	500
Итого	-	1000	1,0	-	229000	1000

Задача 3.20

Имеются условные данные о штабелях бревен (табл. 3.13). Определите среднюю площадь сечения бревна.

Таблица 3.13 - Данные о штабелях бревен

Показатель	Штабель бревен
	№1	№2	№3	№4
Радиус бревен в штабеле (r), см	10	12	15	20
Количество бревен (f), шт	200	100	600	100

Задача 3.21

По данным ряда распределения прядильного оборудования хлопчатобумажного комбината по времени эксплуатации (табл. 3.14) определите структурные средние:

Таблица 3.14 – Данные о работе прядильного оборудования

Возрастная группа оборудования, лет	Количество единиц оборудования, n
До 4	10
4-8	25
8-12	45
12 и больше	20
Всего	100

Контрольные вопросы

1. Что называют статистическим показателем?

2. Виды статистических показателей.

3. Какие требования предъявляют к статистическим показателям?

4. Что характеризуют абсолютные величины; их виды.

5. Что характеризуют относительные статистические величины; способы их представления.

6. Как классифицируются относительные величины?

7. Дать характеристику видам относительных величин.

8. Какое значение имеет средняя величина в статистике?

9. Виды и формы средних величин.

10. В каких случаях используется средняя арифметическая, средняя гармоническая, средняя квадратичная, средняя геометрическая?

11. Расскажите об основных свойствах средней арифметической.

12. Как вычисляется средняя арифметическая по сгруппированным данным?

13. Какие задачи решают структурные средние?

14. В чем заключаются особенности расчета медианы на основе дискретных и интервальных рядов динамики?

15. Как определить моду на основе несгруппированных данных и вариационных рядов распределения?

Практическая работа №4

Вычисление показателей вариации по вариационному ряду распределения

Цель работы – изучить виды абсолютных и относительных показателей вариации, особенности их интерпретации.

Вариацией признака называют отличие в численных значениях признаков единиц совокупности и их колебания около средней величины, что и будет характеризовать совокупность. Чем меньше вариация, тем более однородна совокупность и более надежна (типична) средняя величина.

Для измерения вариации в статистике используются абсолютные и относительные показатели.

К абсолютным показателям вариации относятся:

- размах вариации R,

- среднее линейное отклонение d ,

- средний квадрат отклонений (дисперсия) ,

- среднее квадратическое отклонение .

Размах вариации R является наиболее простым показателем вариации, рассчитывается по формуле: R = x _max − x _min

Этот показатель представляет собой разность между максимальным и минимальным значениями признаков и характеризует разброс элементов совокупности.

Среднее линейное отклонение d является более строгой характеристикой вариации признака, учитывающей различия всех единиц изучаемой совокупности. Среднее линейное отклонение представляет собой среднюю арифметическую абсолютных значений отклонений отдельных вариантов от их средней арифметической. Этот показатель рассчитывается по формулам простой и взвешенной средней арифметической:

- для несгруппированных данных;

- для сгруппированных данных.

В практических расчетах среднее линейное отклонение используется для оценки ритмичности производства, равномерности поставок.

Дисперсия признака представляет собой средний квадрат отклонений вариантов от их средней величины, является общепринятой мерой вариации. В зависимости от исходных данных дисперсия вычисляется по формулам простой и взвешенной средней арифметической:

для несгруппированных данных ;

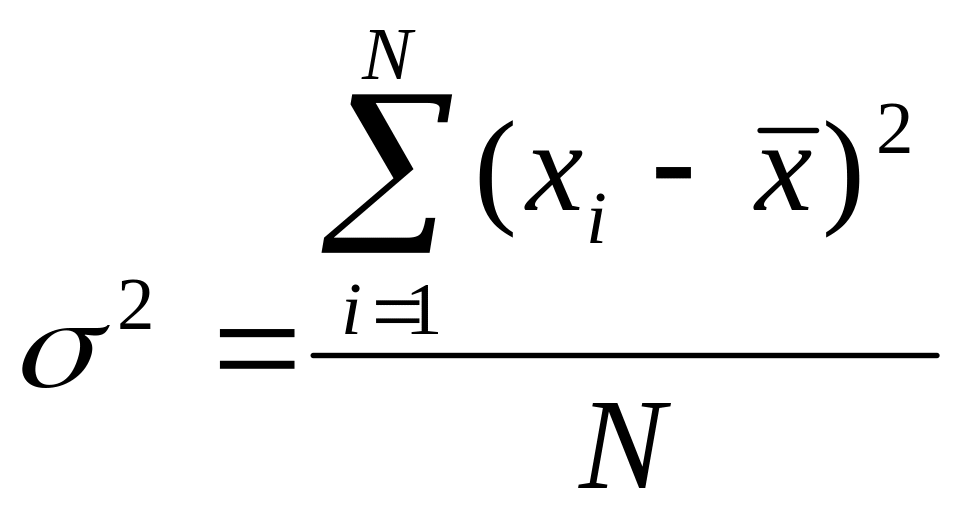для сгруппированных данных .

Среднее квадратическое отклонение представляет собой среднюю квадратическую из отклонений отдельных значений признака от их средней арифметической:

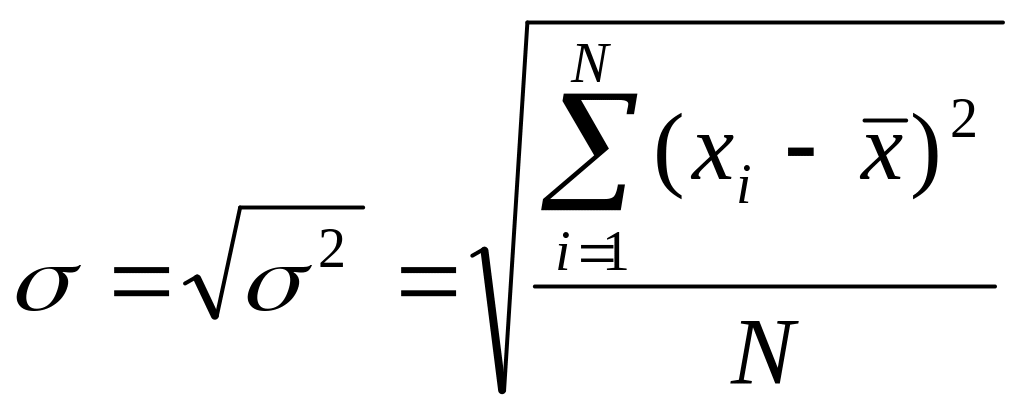для несгруппированных данных

для сгруппированных данных

Среднее квадратическое отклонение является именованной величиной, имеет размерность усредняемого признака, экономически хорошо интерпретируется. Она также используется для оценки надежности средней: чем меньше cреднее квадратическое отклонение , тем надежнее cреднее значение признака x, тем лучше средняя представляет исследуемую совокупность.

Относительные показатели вариации предназначены для оценки и сравнения вариации нескольких признаков по одной совокупности или же вариации одного и того же признака по нескольким совокупностям. Базой для их исчисления является средняя арифметическая.

Самым распространенным относительным показателем вариации является коэффициент вариации . Он представляет собой отношение среднего квадратического отклонения к средней арифметической, выраженное в процентах:

Коэффициент вариации используется для характеристики однородности исследуемой совокупности. Статистическая совокупность считается количественно однородной, если коэффициент вариации не превышает 33% .

Упражнения и задачи

Задача 4.1

По данным ряда распределения прядильного оборудования хлопчатобумажного комбината по времени эксплуатации (табл. 4.1) определите показатели вариации:

Таблица 4.1 – Исходные данные

Возрастная группа оборудования, лет	Количество единиц оборудования, n
До 4	10
4-8	25
8-12	45
12 и больше	20
Всего	100

Задача 4.2

По данным распределения работников предприятия по стажу (табл. 4.2) определите показатели вариации (размах вариации, линейное, квадратическое отклонение, дисперсию, коэффициент вариации):

Таблица 4.2 – Исходные данные

Стаж работы, лет	До 1	1-2	2-3	3-5	5-7	7-9	Более 9
Количество работников	4	6	5	17	18	15	11

Задача 4.3

Средняя величина трудоемкости изделия равна 20 чел./час., а коэффициент вариации 25%. Определите дисперсию.

Задача 4.4

Имеются данные (табл. 4.3) о времени обработки деталей рабочими двух бригад.

Таблица 4.3 – Исходные данные

Бригады	Время обработки деталей, мин
I-я бригада	74	86	112	116	132	134	155	183	-	-
II-я бригада	108	113	114	121	122	126	130	132	135	139

1. Определите показатели центральной тенденции (среднюю величину и медиану).

2. Определите показатели вариации.

Задача 4.5

Сравните вариацию урожайности зерновых культур и картофеля в хозяйствах региона на основе следующих данных (табл. 4.4).

Таблица 4.4 – Исходные данные

№ хозяйства	Урожайность, ц/га		Посевная площадь, га
	Зерновых Y	Картофеля X	Зерновых Y	Картофеля Х
1	15	170	20	10
2	20	90	30	20
3	13	130	10	50
4	17	150	90	40
5	25	120	50	30
6	14	80	20	25
7	16	60	32	20
8	27	160	48	45
9	33	140	25	70
10	30	100	30	35
Итого			355	345

Задача 4.6

В трех партиях продукции, представленных на контроль качества, было обнаружено:

а) первая партия – 1000 изделий, из них 800годных, 200 бракованных;

б) вторая партия – 800 изделий, из них 720 годных, 80 бракованных;

в) третья партия – 900 изделия, из них годных 855, бракованны 45 единиц продукции.

Определить в целом для всех партий следующие показатели:

а) средний процент годной продукции и средний процент брака;

б) дисперсию, среднее квадратичное отклонение и коэффициент вариации годной продукции.

Контрольные вопросы

1. В чем суть вариации и необходимости ее определения при статистическом изучении?

2. Виды основных показателей вариации.

3. Абсолютные показатели вариации и их экономическое толкование.

4. Относительные показатели вариации и их экономическое толкование.

5. Что такое размах вариации и в чем его особенности как показателя вариации?

6. В чем состоят особенности расчета показателей вариации по сгруппированным данным?

7. Какое аналитическое значение имеет коэффициент вариации?

8. Что представляет собой дисперсия альтернативного признака?

9. В чем заключается правило сложения дисперсий и суть составляющих общей дисперсии?

10. Как определяется внутригрупповая дисперсия?

11. Что характеризует межгрупповая дисперсия, формула ее расчета?

Практическая работа №5

Определение ошибки выборки, объема выборки, пределов характеристики

генеральной совокупности

Цель работы – изучить сущность выборочного наблюдения и основные его характеристики; принципы, способы и методы формирования выборочной совокупности; виды ошибок выборочного наблюдения; способы оценки результатов наблюдения и приёмы распространения их на генеральную совокупность. Научиться формировать выборочную совокупность; определять параметры генеральной и выборочной совокупности; рассчитывать ошибки выборки и необходимый объём повторного и бесповторного отбора; оценивать точность проведённого наблюдения.

Выборочным называется такое статистическое исследование, при котором обобщающие показатели изучаемой совокупности устанавливаются по некоторой ее части, сформированной на основе положений случайного отбора.

Случайный отбор может быть повторным или бесповторным.

- При повторном отборе статистические единицы, отобранные ранее, возвращаются в генеральную совокупность и могут вновь попасть в выборку.

При этом численность генеральной совокупности при проведении отбора остается постоянной, тем самым обеспечивается каждой статистической единице равная возможность попасть в выборку

- При бесповторном отборе единицы не возвращаются обратно в генеральную совокупность, ее численность с каждой единицей сокращается, абсолютно равная возможность каждой статистической единице попасть в выборку полностью не обеспечивается. Но при этом при одном и том же объеме выборки наблюдение охватывает больше единиц генеральной совокупности, что обеспечивает более точные результаты по сравнению с повторным отбором (меньшую ошибку выборки).

Бесповторный отбор находит более широкое применение на практике. Повторный отбор используется в тех случаях, когда нельзя применить бесповторную выборку; например, при обследовании потребительского спроса, изучении общественного мнения по какому-либо вопросу и т. п.

В общем случае под ошибкой выборки понимают объективно возникающее расхождение между характеристиками выборки и генеральной совокупности.

, где ,

х_i – вариант (значение варьирующего признака)

f_i – частота, вес

N – объем генеральной совокупности ( = сумме f_i)

х_i – вариант (значение варьирующего признака)

t_i – частота, вес

n – объем выборочной совокупности

В математической статистике доказывается, что средняя ошибка выборки определяется по формуле: ,

где - дисперсия генеральной совокупности;

n – объем выборочной совокупности.

На практике показатель дисперсии по генеральной совокупности заменяют на аналогичный показатель по выборочной совокупности на базе закона больших чисел. По этому закону выборочная совокупность при достаточно большом ее объеме точно воспроизводит характеристики генеральной совокупности.

Следовательно, , где

- выборочная дисперсия количественного признака, .

n – объем выборочной совокупности.

Средняя ошибка выборки для доли определяется по формуле: , где

- выборочная дисперсия доли альтернативного признака,

Формулы средней ошибки выборки при бесповторном отборе принимают вид:

• для средней количественного признака

• для доли альтернативного признака

Ошибка выборки, исчисленная с заданной степенью вероятности, называется предельной ошибкой выборки.

Предельная ошибка выборки является максимально возможной при данной вероятности ошибкой. Это означает, что с заданной вероятностью гарантируется, что ошибка любой выборки не превысит предельную ошибку. Такая вероятность называется доверительной.

Предельная ошибка выборки рассчитывается по формуле: ,

где t – коэффициент доверия, значения которого определяются доверительной вероятностью F(t) .

Значения коэффициента доверия t задаются в таблицах нормального распределения вероятностей. Чаще всего используются следующие сочетания:

t	F(t)
1	0,683
1,5	0,866
2	0,954
2,5	0,988
3	0,997
3,5	0,999

Так, если t = 1, то с вероятностью 0,683 можно утверждать, что расхождение между выборочными характеристиками и параметрами генеральной совокупности не превысит одной средней ошибки.

Предельные ошибки выборки для разных параметров при разных методах отбора статистических единиц рассчитываются по формулам, приведенным в таблице 5.1.

Таблица 5.1 – Формулы расчета предельных ошибок выборки при собственно-случайном отборе единиц выборочной совокупности

Метод отбора	Предельные ошибки выборки
	Для средней характеристики	Для доли
Повторный
Бесповторный

Зная величину предельной ошибки выборки, можно рассчитать интервалы, в которых будут находиться характеристики генеральной совокупности:

Пределы, в которых с данной степенью вероятности будет заключена неизвестная величина изучаемого показателя в генеральной совокупности, называют доверительными интервалами, а вероятность F(t) – доверительной вероятностью. Чем выше значение ошибки выборки , тем больше величина доверительного интервала и, следовательно, ниже точность оценки.

При определении средней ошибки механической выборки используются формулы средней ошибки при собственно-случайном бесповторном отборе.

Среднюю ошибку типической выборки при повторном отборе определяют по формулам:

- для средней количественного признака

, где - средняя из внутригрупповых выборочных дисперсий;

- для доли альтернативного признака

- средняя из внутригрупповых дисперсий доли альтернативного признака по выборке.

При бесповторном отборе среднюю ошибку типической выборки рассчитывают по следующим формулам:

-для средней количественного признака

- для доли альтернативного признака

Средняя ошибка серийной выборки при повторном отборе определяется следующим образом:

- для средней количественного признака:

,

где ,

- среднее i-той серии;

- средняя по всей выборке;

r – число отобранных серий.

- для доли альтернативного признака:

, где - межгрупповая дисперсия доли серийной выборки;

- доля признака в i-той группе;

- общая доля признака во всей выборке.

При бесповторном отборе средняя ошибка серийной выборки может быть определена:

- для средней количественного признака:

, где R – общее число серий в генеральной совокупности.

- для доли альтернативного признака:

Численность выборки – один из факторов, влияющих на величину ее ошибки: чем она больше, тем меньше ошибка. С другой стороны, с объемом выборки связаны затраты на проведение исследования: чем она больше, тем больше затраты.

Таблица 5.2 – Формулы определения численности выборки при разных методах отбора

Вид выборочного наблюдения	Повторный отбор	Бесповторный отбор
Собственно - случайная выборка:
а) при определении среднего размера признака
б) при определении доли признака
Механическая выборка	То же	То же
Типичная выборка:
а) при определении среднего размера признака
б) при определении доли признака
Серийная выборка:
а) при определении среднего размера признака
б) при определении доли признака

Малой выборкой называется такое выборочное наблюдение, численность единиц которого не превышает 30.

При оценке результатов малой выборки величина генеральной совокупности не используется. Для определения возможных пределов ошибки пользуются критерием Стьюдента, определяемым по формуле:

, где

- средняя ошибка малой выборки.

Величина вычисляется на основе данных выборочного наблюдения: .

Данная величина используется лишь для исследуемой совокупности, а не в качестве приближенной оценки в генеральной совокупности.

Предельная ошибка малой выборки ( ) в зависимости от средней ошибки( ) представляется как

Однако для малой выборки величина коэффициента доверия t по другому связана с вероятностной оценкой, чем при большой выборке (так как, закон распределения отличается от нормального). Согласно установленному Стьюдентом закону распределения, вероятная ошибка распределения зависит как от величины коэффициента доверия t , так и от объема выборки. В таблице 5.3 приведен фрагмент таблицы распределения Стьюдента.

Таблица 5.3 - Распределение вероятностей в малых выборках в зависимости от

коэффициента доверия t и объема выборки

n	t
	4	5	6	7	8	9	10	15	20
0,5	348	356	362	366	368	370	372	376	378	383
1,0	608	626	636	644	650	654	656	666	670	683
1,5	770	792	806	816	832	828	832	846	850	865
2,0	860	884	908	908	914	920	924	932	940	954
2,5	933	946	955	959	963	966	968	975	978	988
3,0	942	960	970	976	980	938	984	992	992	977

Упражнения и задачи

Задача 5.1

Для определения среднего возраста 1200 студентов факультета необходимо провести выборочное обследование методом случайного бесповтороного отбора. Предварительно установлено, что среднее квадратическое отклонение возраста студентов равно 10 годам . Сколько студентов нужно обследовать, чтобы с вероятностью 0,954 средняя ошибка выборки не превышала 3 года?

Задача 5.2

В цехе предприятия 10 бригад рабочих. С целью изучения их производительности труда была осуществлена 20%-ная серийная выборка, в которую попали 2 бригады. В результате обследования установлено, что средняя выработка рабочих в бригадах составила 4,6 и 3 тонн. С вероятностью 0,997 определить пределы, в которых будет находиться средняя выработка рабочих цеха.

Задача 5.3

Методом собственно случайной 10 %-ной выборки обследована жирность молока у 100 коров. По данным выборки средняя жирность молока оказалась равной 3,64%, а дисперсия составила 2,56. Определить: 1) среднюю ошибку выборки; 2) с вероятностью, равной 0,954, предельные значения генеральной средней

Задача 5.4

Как изменится величина ошибки бесповторной выборки, если объем увеличится с 5 до 25%.

Задача 5.5

Для определения среднего возраста мужчин, вступающих в брак, в районе была проведена 5%-ная типическая выборка с отбором единиц пропорционально численности типических групп. Внутри групп применялся механический отбор.

Данные по выборке представлены в таблице 5.4:

Таблица 5.4 – Исходные данные

Соц. группа	Число мужчин, ni	Ср. возраст, xi	Среднее квадратическое отклонение,	Доля мужчин, вступивших во второй брак , %, wi
Рабочие	60	24	5	10
Служащие	40	27	8	20

С вероятностью 0,954 определить пределы, в которых будет находиться средний возраст мужчин, вступающих в брак, и долю мужчин, вступающих в брак во второй раз.

Задача 5.6

На основе выборочного обследования методом простой случайной выборки 600 рабочих одной из отраслей промышленности установлено (повторный отбор), что удельный вес численности женщин составил 0,4. С какой вероятностью можно утверждать, что при определении доли женщин, занятых в этой отрасли, допущена предельная ошибка выборки, не превышающая 5%?

Задача 5.7

Среди выборочно обследованных 1000 семей региона по уровню дохода ( выборка 2%-ная, механическая) малообеспеченных оказалось 300 семей. Требуется с вероятностью 0,997 определить долю малообеспеченных семей в регионе.

Задача 5.8

Сколько рабочих завода нужно обследовать в порядке случайной повторной выборки для определения средней заработной платы, чтобы с вероятностью, равной 0,954, можно было бы гарантировать ошибку в размере не более 5 рублей? Предполагаемое среднее квадратическое отклонение

Задача 5.9

Для определения урожайности зерновых культур проведено выборочное обследование 100 хозяйств региона различных форм собственности, в результате которого получены сводные данные (табл. 5.5):

Таблица 5.5 – Исходные данные

Хозяйства	Кол-во обследованных хозяйств (f)	Средняя урожайность, ц/га (xi)	Дисперсия урожайности в каждой группе, ( )
Коллективные	30	18	15
ОАО	50	20	25
Фермерские	20	28	40
Итого	100

Необходимо с вероятностью 0,954 определить предельную ошибку выборочной средней и доверительные пределы средней урожайности зерновых культур по всем хозяйственным регионам.

Задача 5.10

Для определения среднего срока пользования краткосрочным кредитом в банке было произведена 5%-ая механическая выборка, в которую попало 100 счетов. В результате обследования установлено, что средний срок пользования краткосрочным кредитом – 30 дней при среднем квадратическом отклонении 9 дней. В пяти счетах срок пользования кредитом превышал 60 дней. С вероятностью 0,954 определить пределы, в которых будут находиться срок пользования краткосрочным кредитом в генеральной совокупности и доля счетов со сроком пользования краткосрочным кредитом более 60 дней.

Задача 5.11

По городской телефонной сети в порядке случайной выборки (механической) отбор произвели 100 наблюдений и установили среднюю продолжительность одного телефонного разговора 5 мин., при среднем квадратическом отклонении 2 мин.

Какова вероятность того, что ошибка репрезентативности при определении средней продолжительности телефонного разговора не превысит 18 сек.?

Задача 5.12

Для определения зольности угля в порядке случайной выборки было обследовано 100 проб угля. В результате обследования установлено, что средняя зольность угля в выборке 16%, среднее квадратическое отклонение 5%. В десяти пробах зольность угля составила более 20%. С вероятностью 0,954 определить пределы, в которых будут находиться средняя зольность угля в месторождении и доля угля с зольностью более 20%.

Задача 5.13

На предприятии в порядке случайной бесповторной выборки было опрошено 100 рабочих из 1000 и получены следующие данные об их доходе за октябрь:

Месячный доход, руб. Число рабочих

600-1000 12

1000-1400 60

1400-1800 20

1800-2200 8

Определить: 1) среднемесячный размер дохода у работников данного предприятия, гарантируя результат с вероятностью 0,997; 2) долю рабочих предприятия, имеющих месячный доход 1400 руб. и выше, гарантируя результат с вероятностью 0,954; 3) необходимую численность выборки при определении среднего месячного дохода работников предприятия, чтобы с вероятностью 0,954 предельная ошибка выборки не превышала 50 руб.; 4) необходимую численность выборки при определении доли рабочих с размером месячного дохода 1400 руб. и выше, чтобы с вероятностью 0,954 предельная ошибка не превышала 4%.

Задача 5.14

В каком соотношении находится (при прочих равных условиях) ошибки случайной повторной и случайной бесповторной выборок при 10% отборе?

Задача 5.15

Из партии изготовленных изделий общим объемом 2000 единиц проверено посредством механической выборки 30% изделий, из которых бракованными оказались 12 изделий.

Определить: 1) долю бракованных изделий по данным выборки; 2) пределы, в которых находится процент бракованных изделий, для всей партии (с вероятностью 0,954)

Задача 5.16

По данным выборочного обследования 10 000 пассажиров пригородного сообщения средняя дальность поездки пассажира составила 35,5 км, а среднее квадратическое отклонение – 16,0 км.

Определить: 1) пределы средней дальности поездки пассажиров с вероятностью 0,954; 2) как изменится предельная ошибка выборки, если вероятность будет принята равной 0,997?

Задача 5.17

Объем выборки увеличился в 2 раза. Определить, как изменится ошибка простой случайной повторной выборки.

Задача 5.18

Какова должна быть численность механической выборки для определения доли служащих, прошедших повышение квалификации по использованию вычислительной техники, чтобы с вероятностью 0,954 ошибка репрезентативности не превышала 10%? Общая численность служащих предприятия составляет 324 человека.

Задача 5.19

Сколько фирм необходимо проверить налоговой инспекции района, чтобы ошибка доли фирм, несвоевременно уплативших налоги, не превысила 5%? По данным предыдущей проверки, доля таких фирм составила 32%. Доверительную вероятность принять равной 0,954.

Контрольные вопросы

1. Сущность и значение выборочного метода как разновидности несплошного статистического наблюдения.

2. Случаи использования выборочного метода.

3. Проявление закона больших чисел и теории вероятности в выборочном обследовании.

4. Различие повторного и бесповторного отбора.

5. Преимущества выборочного метода как разновидности несплошного статистического наблюдения.

6. Недостатки выборочного метода как разновидности несплошного статистического наблюдения.

7. Виды ошибок в данных выборочного наблюдения.

8. Средняя и предельная ошибки выборки.

9. Показатель доли, расчет средней и предельной ошибок для доли, определение доверительных интервалов.

10. Теоретическое и практическое обоснование объема выборки.

11. Характеристика простой случайной выборки, формулы расчета предельных ошибок и объема выборки.

12. Расслоенная (типическая) выборка, формулы расчета предельных ошибок и объема выборки.

13. Механическая выборка, формулы расчета предельных ошибок и объема выборки.

14. Серийная (гнездовая) выборка, формулы расчета предельных ошибок и объема выборки.

15. Характеристика малой и комбинированной выборок.

Практическая работа №6

Исчисление основных показателей динамики. Сглаживание рядов динамики методами скользящей средней и аналитического выравнивания.

Определение показателей сезонности

Цель работы – изучить классификацию рядов динамики, правила их построения; возможные причины несопоставимости уровней и приёмы их устранения; абсолютные, относительные и средние показатели динамики и методику их расчёта; методы укрупнения интервалов, скользящей средней, аналитического выравнивания; индексы сезонности; методы прогнозирования на основе динамических рядов. Научиться строить временные ряды и приводить их к сопоставимому виду; используя соответствующие показатели и методы анализировать скорость и интенсивность изменения уровней временных рядов; правильно определять средние показатели динамики; выявлять основную тенденцию динамики и влияние сезонного фактора; строить краткосрочные прогнозы на основе динамики изучаемого явления.

Ряды динамики представляют собой ряды изменяющихся во времени значений статистического показателя, расположенного в хронологическом порядке.

Составными элементами ряда динамики являются показатели уровней ряда и периоды времени (годы, кварталы, месяцы, сутки ) или моменты (даты ) времени.

Уровни ряда обычно обозначаются через "У", периоды времени или моменты через " t".

Ряд динамики, хронологический ряд, динамический ряд, временной ряд – это последовательность упорядоченных во времени числовых показателей, характеризующих уровень развития изучаемого явления. Всякий ряд динамики включает, следовательно, два обязательных элемента: во-первых, время и, во-вторых, конкретное значение показателя, или уровень ряда. Ряды динамики различаются по следующим признакам.

1. По времени – интервальные и моментные ряды. Интервальный ряд динамики – последовательность, в которой уровень явления относится к результату, накопленному или вновь произведенному за определенный интервал времени (например за сутки, месяц, год и. т. п.). Таковы, например, ряды показателей объема продукции по месяцам года, количества отработанных человеко-дней по отдельным периодам и т.д. Если же уровень ряда показывает фактическое наличие изучаемого явления в конкретный момент времени (на начало месяца, квартала, года и т. п.), то совокупность уровней образует моментный ряд динамики. Примерами моментных рядов могут быть последовательности показателей численности населения на начало года, величины запаса какого-либо материала на начало периода и т.д.

Особенность интервального ряда состоит в том, что его уровни характеризуют собой суммарный итог какого либо явления за определенный отрезок времени. Они зависят от продолжительности этого периода времени, их можно суммировать, как не содержащие повторного счета.

Особенность моментного ряда состоит в том, что его уровни, как правило, содержат элементы повторного счета, например число вкладов населения, учитываемых за январь, существует и в настоящее время, являясь единицами совокупности в июне. В результате чего суммировать уровни ряда не целесообразно.

2. По форме представления уровней – ряды абсолютных, относительных и средних величин.

3. По расстоянию между датами или интервалам времени выделяют полные и неполные хронологические ряды.

Полные ряды динамики имеют место, когда даты регистрации или окончания периодов следуют друг за другом с равными интервалами, это равноотстоящие ряды динамики. Неполные – когда принцип равных интервалов не соблюдается.

Статистические данные должны быть сопоставимы по территории, кругу охватываемых объектов, единицам измерения, времени регистрации, ценам, методологии расчета.

Числовые уровни рядов динамики должны быть упорядоченными во времени. Не допускается анализ рядов с пропусками отдельных уровней, если же такие пропуски неизбежны, то их восполняют условными расчетными значениями.

При изучении явления во времени перед исследователем встает проблема описания интенсивности изменения и расчета средних показателей динамики. Решается она путем построения соответствующих показателей. Для характеристики интенсивности изменения во времени такими показателями будут: абсолютный прирост, темпы роста, темпы прироста, абсолютное значение одного процента прироста.

Расчет показателей динамики представлен в таблице 6.1.

Таблица 6.1 – Алгоритм расчета показателей динамики

Показатель	Базисный	Цепной
Абсолютный прирост	Yi-Y0	Yi-Yi-1
Коэффициент роста (Кр)	Yi : Y0	Yi : Yi-1
Темп роста (Тр)	(Yi : Y0)×100	(Yi : Yi-1)×100
Коэффициент прироста (Кпр )
Темп прироста (Тпр)
Абсолютное значение одного процента прироста (А)

Система средних показателей динамики включает:

Средний уровень ряда – это показатель, обобщающий итоги развития явления за единичный интервал или момент из имеющейся временной последовательности. Расчет среднего уровня ряда динамики определяется видом этого ряда и величиной интервала, соответствующего каждому уровню.

Для интервальных рядов с равными периодами времени средний уровень рассчитывается следующим образом:

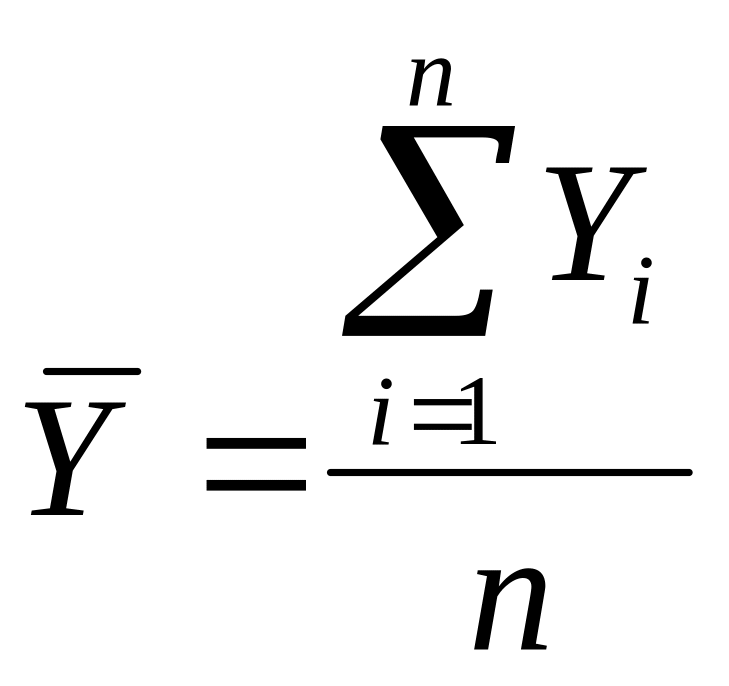
где n– общая длина временного ряда или общее число равных временных отрезков, каждому из которых соответствует свой уровень Y_i (1 = 1, 2, ..., n).

Для моментных рядов с равностоящими уровнями средний уровень рассчитывается в предположении, что в пределах каждого периода, разделяющего моментные наблюдения, развитие явления происходило по линейному закону. Тогда общий средний уровень вычисляется по формуле средней хронологической:

.

Средний абсолютный прирост показывает, на сколько единиц в среднем увеличивался или уменьшался каждый уровень ряда по сравнению с предыдущим за ту или иную единицу времени (в среднем ежемесячно, ежегодно и т.п.).

Средний абсолютный прирост характеризует среднюю абсолютную скорость роста (или снижения) уровня ряда. Его рассчитывают в зависимости от исходных данных следующими способами:

1. как простую среднюю арифметическую из абсолютных приростов (цепных) за последовательные промежутки времени: ;

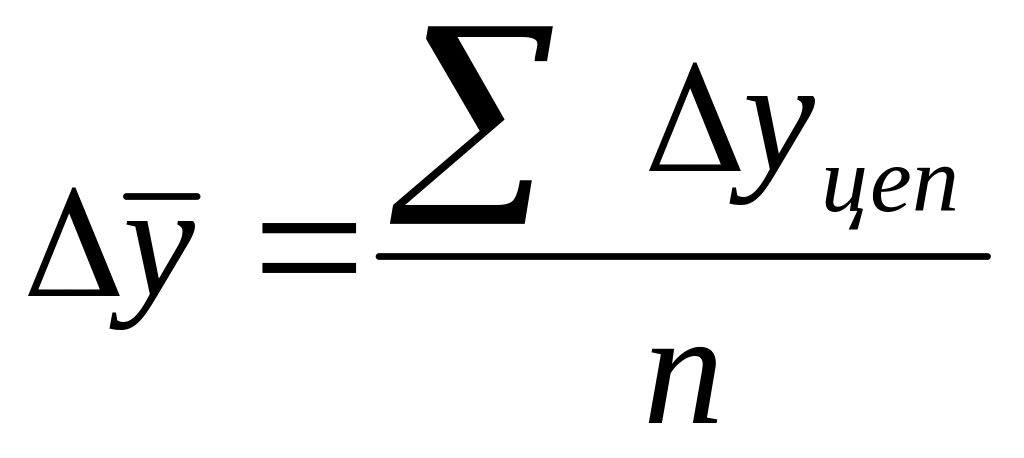2. как частное от деления базисного абсолютного прироста конечного уровня ряда на продолжительность периода: ;

3. через накопленный (базисный) абсолютный прирост: .

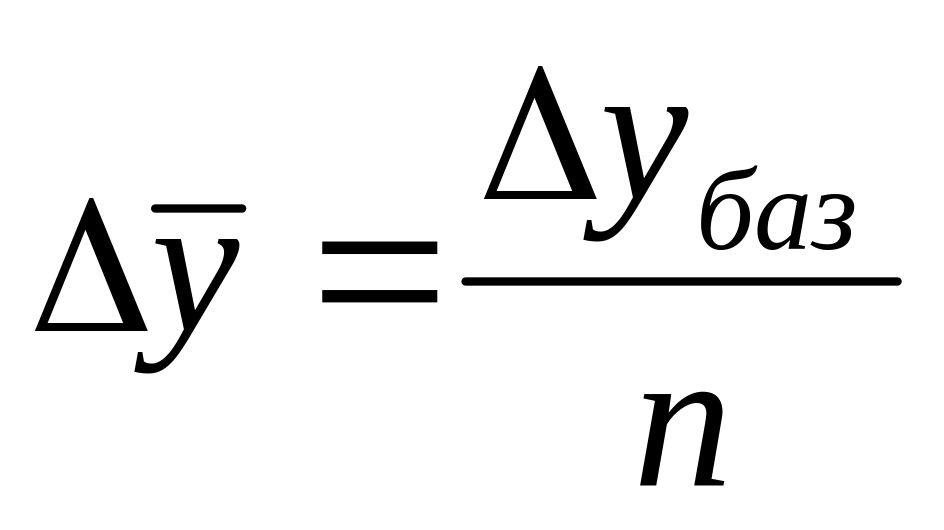Средний коэффициент роста (снижения) показывает, во сколько раз в среднем за единицу времени изменяется уровень ряда динамики. Для его вычисления используется формула средней геометрической в предположении, что соблюдается равенство фактического отношения конечного уровня к начальному при замене фактических темпов на средние. В зависимости от наличия исходных данных расчет проводят следующим образом:

1. если исходной информацией служат цепные коэффициенты роста, то формула имеет вид: 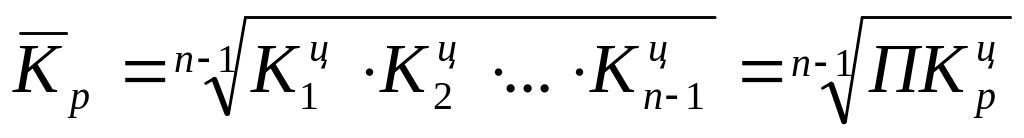, где П – произведение цепных показателей динамики.

2. Через базисный коэффициент роста конечного периода: ;

3. Если известны уровни динамического ряда:

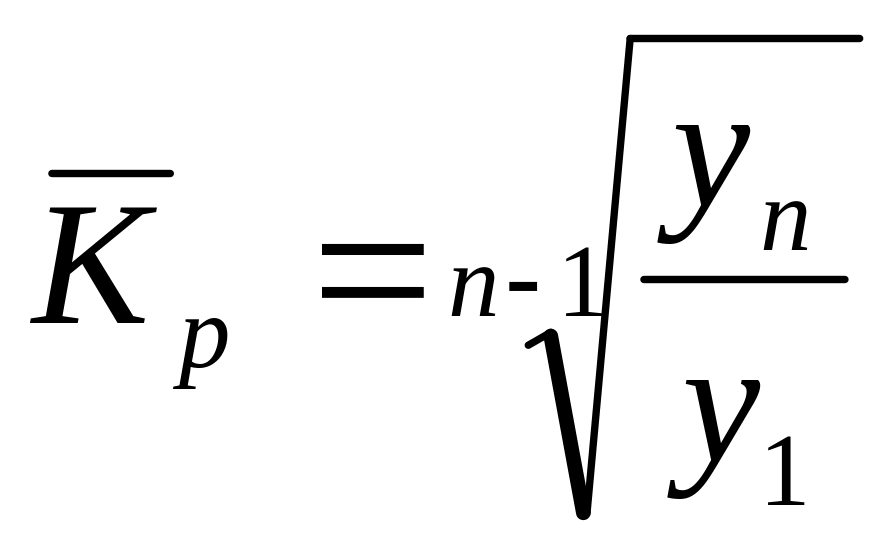
Средний темп роста представляет собой средний коэффициент роста, выраженный в процентах . Отсюда средний темп прироста .

Всякий ряд динамики теоретически может быть представлен в виде:

- тренда – основной тенденции развития динамического ряда (к увеличению либо снижению его уровней);

- циклических (периодических) колебаний, в том числе сезонных;

- случайных колебаний.

Изучение тренда включает два основных этапа:

1) ряд динамики проверяется на наличие тренда;

2) производится выравнивание временного ряда и непосредственное выделение тренда с экстраполяцией полученных результатов.

Непосредственное выделение тренда может быть произведено тремя методами.

1. Укрупнение интервалов. Ряд динамики разделяют на некоторое достаточно большое число равных интервалов. Если средние уровни по интервалам не позволяют увидеть тенденцию развития явления, переходят к расчету уровней за большие промежутки времени, увеличивая длину каждого интервала (одновременно уменьшается количество интервалов).

2. Скользящая средняя. В этом методе исходные уровни ряда заменяются средними величинами, которые получают из данного уровня и нескольких симметрично его окружающих. Целое число уровней, по которым рассчитывается среднее значение, называют интервалом сглаживания. Интервал может быть нечетным (3, 5, 7 и т.д. точек) или четным (2, 4, 6 и т.д. точек).

При нечетном сглаживании полученное среднее арифметическое значение закрепляют за серединой расчетного интервала, при четном этого делать нельзя. Поэтому при обработке ряда с четными интервалами их искусственно делают нечетными, для чего образуют ближайший больший нечетный интервал, но из крайних его уровней берут только 50%.

Недостаток методики сглаживания скользящими средними состоит в условности определения сглаженных уровней для точек в начале и конце ряда. Получают их специальными приемами – расчетом средней арифметической взвешенной.

3. Аналитическое выравнивание. Под этим понимают определение основной проявляющейся во времени тенденции развития изучаемого явления. Развитие предстает перед исследователем как бы в зависимости только от течения времени. В итоге выравнивания временного ряда получают наиболее общий, суммарный, проявляющийся во времени результат действия всех причинных факторов. Отклонение конкретных уровней ряда от уровней, соответствующих общей тенденции, объясняют действием факторов, проявляющихся случайно или циклически. В результате приходят к трендовой модели

,

где f(t) – уровень, определяемый тенденцией развития;

– случайное и циклическое отклонение от тенденции.

Целью аналитического выравнивания динамического ряда является определение аналитической или графической зависимости f(t). На практике по имеющемуся временному ряду задают вид и находят параметры функции f(t), а затем анализируют поведение отклонений от тенденции. Функцию f(t) выбирают таким образом, чтобы она давала содержательное объяснение изучаемого процесса.

Чаще всего при выравнивании используются следующие зависимости:

линейная ;

параболическая ;

экспоненциальные

Линейная зависимость выбирается в тех случаях, когда в исходном временном ряду наблюдаются более или менее постоянные абсолютные цепные приросты, не проявляющие тенденции ни к увеличению, ни к снижению.

Параболическая зависимость используется, если абсолютные цепные приросты сами по себе обнаруживают некоторую тенденцию развития, но абсолютные цепные приросты абсолютных цепных приростов (разности второго порядка) никакой тенденции развития не проявляют.

Экспоненциальные зависимости применяются, если в исходном временном ряду наблюдается либо более или менее постоянный относительный рост (устойчивость цепных темпов роста, темпов прироста, коэффициентов роста), либо, при отсутствии такого постоянства, – устойчивость в изменении показателей относительного роста (цепных темпов роста цепных же темпов роста, цепных коэффициентов роста цепных же коэффициентов или темпов роста и т.п.).

Оценка параметров (а₀,а₁,а₂) осуществляется преимущественно методом наименьших квадратов, который обеспечивает наименьшую сумму квадратов отклонений фактических уровней от выровненных:

Математический аппарат метода наименьших квадратов описан в математической статистике. Так, решение системы нормальных уравнений в результате минимизации квадратов отклонений фактических уровней динамического ряда от их выровненного значения, позволяет отыскать параметры а₀,а₁,а_2.

Например, система нормальных уравнений для нахождения параметров прямой:

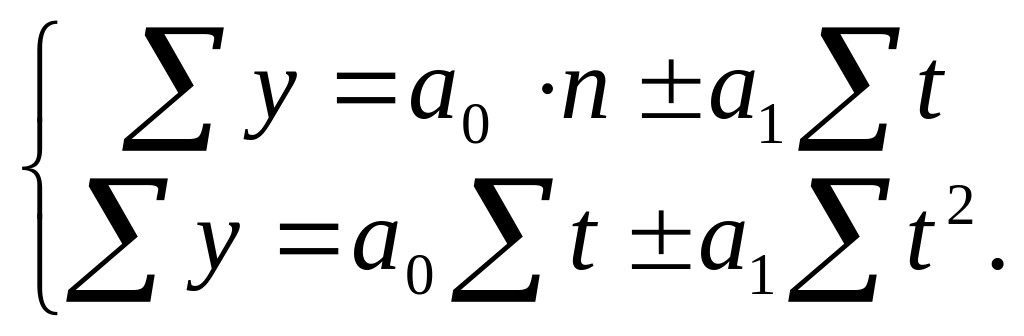
для параболы 2-го порядка:

Для упрощения расчетов допускается перенос начала координат в середину ряда динамики. Это позволяет упростить сами нормальные уравнения, а также уменьшить абсолютные значения величин, участвующих в расчете. Если до переноса начала координат t было равно 1,2,3,…, то после переноса:

- для четного числа членов ряда t =…,-5; -3; -1; 1; 3; 5;…

- для нечетного числа членов ряда t = …, -3; -2; -1; 0; 1; 2; 3; …

В этом случае оценка параметров функции имеет вид:

Для прямой: .

Сезонными называют периодические колебания, возникающие под влиянием смены времени года и других причин природного или социально-культурного порядка. Они имеют устойчивый характер, повторяются регулярно с интервалом в один год.

В статистике существует ряд методов изучения и измерения сезонных колебаний:

а) метод абсолютных разностей;

б) метод относительных разностей;

в) построение индексов сезонности;

г) построение аналитических моделей.

По методу абсолютных разностей сезонные колебания характеризуются величинами:

,

где - абсолютное отклонение фактических уровней или средних месячных (квартальных) уровней от общей средней или трендового i-го уровня .

По методу относительных разностей сезонные колебания описываются зависимостью и могут быть выражены в относительных величинах или процентах.

Метод построения «сезонной волны» заключается в расчете специальных показателей, которые называются индексами сезонности .

Индексами сезонности называется процентные отношения фактических (эмпирических) внутригрупповых уровней к теоретическим уровням, рассчитанным по трендовому уравнению, либо к средним уровням.

Совокупность индексов сезонности отражают сезонную волну.

Расчет индексов сезонности выполняют двумя методами в зависимости от характера динамики:

- если тренд выражен неявно, то есть годовой уровень явления из года в год остается относительно неизменным, то индексы сезонности рассчитываются методом постоянной средней. Они рассчитываются по формуле:

Индексы сезонности рассчитываются в такой последовательности:

- Рассчитываются средние уровни для каждого одноименного периода ( )по данным за все годы наблюдения.

- Определяется общая средняя за весь период наблюдения.

- Вычисляется индекс сезонности по приведенной выше формуле.

- если тренд выражен явно, то для исчисления индексов сезонности используется метод переменной средней, в соответствии с которым их расчет проводится по формуле:

расчетные (выравненные) уровни динамического ряда.

n – число лет наблюдения.

Совокупность средних индексов сезонности одноименных периодов составляет модель сезонной волны.

Если при построении модели сезонной волны случайные колебания гасятся полностью, то сумма средних индексов сезонности одноименных периодов = 1200%, если уровни брались за месяц, и 400%, если уровни были квартальными. Если это условие не выполняется, то проводится корректировка модели.

Статистическое прогнозирование основано на предположении, что закономерность развития, основная тенденция, действующая в прошлом (внутри ряда динамики), сохранится и в будущем. Такое предположение называется экстраполяцией. Теоретической основой распространения тенденции на будущее является инерционность социально-экономических явлений.

Точечный прогноз представляет собой конкретное численное значение уровня в прогнозируемый период (момент) времени.

Интервальный прогноз – диапазон численных значений, предположительно содержащий прогнозируемое значение уровня.

В зависимости от того, какие принципы и исходные данные положены в основу прогноза, выделяют следующие методы экстраполяции (прогнозирования):

• на основе среднего абсолютного прироста ,

• на основе среднего коэффициента роста ,

• на основе аналитического выравнивания ряда.

Метод прогнозирования на основе среднего абсолютного прироста применяется в том случае, если уровни изменяются равномерно (линейно). Прогнозируемое значение уровня определяется по формуле:

, где

- экстраполируемый уровень;

- конечный уровень ряда динамики;

l – период упреждения прогноза (срок экстраполяции).

Прогнозирование по среднему коэффициенту роста применяется, если общая тенденция характеризуется экспотенциальной кривой. В этом случае экстраполируемый уровень определяется по формуле:

Прогнозирование на основе аналитического выравнивания является наиболее распространенным методом прогнозирования. Для получения прогноза используется аналитическое выражение тренда. Чтобы получить прогноз, достаточно в модели продолжить значение условного показателя времени t_i до t_n+i.

Интервальные прогнозы имеют значительные преимущества перед точечными – они учитывают вероятность свершения прогноза. Величина доверительного интервала определяется в общем виде так:

, где (27)

- коэффициент доверия по распределению Стьюдента;

- средняя квадратическая ошибка тренда, рассчитываемая по формуле:

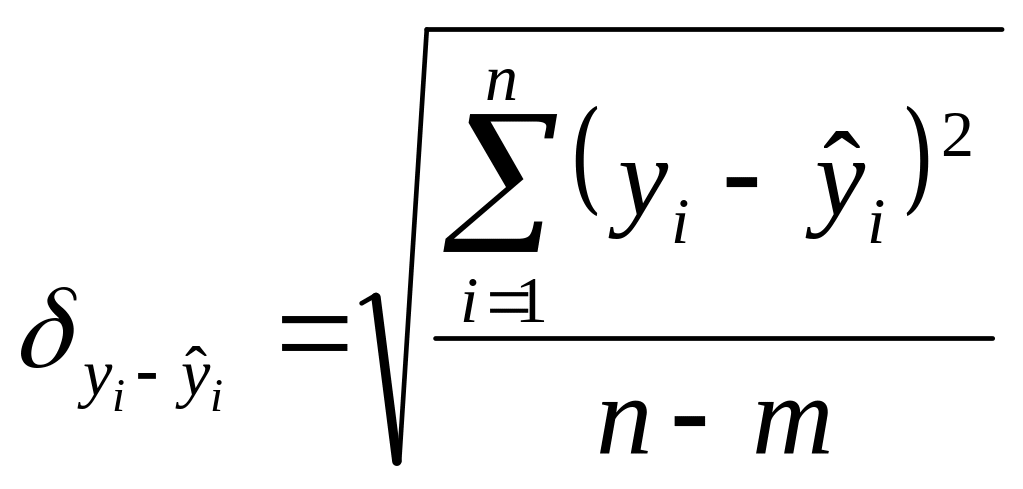
n – число уровней исходного ряда,

m – число параметров трендового уравнения.

Коэффициент доверия выбирается по таблице распределения Стьюдента.

Таким образом, при использовании интервального прогноза:

Упражнения и задачи

Задача 6.1.

Имеются условные данные (табл.6.22) о производстве картофеля в регионе.

Таблица 6.2 - Производство картофеля в регионе (в старых и новых границах), тыс. т.

Показатель	Год
	2004	2005	2006	2007	2008
В границах региона: старых новых	1850,0	1930,5	2020,0 2444,2	2680,9	2800,4

Получить сопоставимый ряд динамики производства картофеля в регионе в новых границах.

Задача 6.2.

Имеются фактические данные (табл. 6.3) о продаже молока и молочных продуктов в регионе за 2008 г.

Таблица 6.3- Продажа молока и молочных продуктов в регионе по кварталам 2008 г., тыс.т

Показатель	Квартал года
	I	II	III	IV
Продано молока и молочных продуктов	336,2	340,7	342,1	359,0

Получить ряд динамики сопоставимых уровней продажи молока и молочных продуктов в регионе.

Задача 6.3.

Имеются данные (табл. 6.4) о производстве яиц в регионе:

Таблица 6.4 - Производство яиц в регионе, млн. шт.

Годы	1	2	3	4	5	6	7	8	9
Млн. шт. Yi	22,6	23,5	23,7	22,1	24,8	26,0	26,7	29,7	30,8

Определите показатели динамики производства яиц в регионе (цепным и базисным способом).

Задача 6.4.

По данным задачи 6.3.:

1. Выявите основную тенденцию производства яиц в регионе.

2. Рассчитайте прогноз производства яиц в регионе на ближайшие 3 года.

Задача 6.5.

Динамика производства пиломатериалов в Брянской области за 2002-2007 гг. характеризуется следующими данными (табл. 6.5):

Таблица 6.5 - Производство пиломатериалов в Брянской области, тыс. м³

	2002	2003	2004	2005	2006	2007
пиломатериалы	137,0	166,7	168,5	176,8	209,3	204,5

Проанализируйте динамику производства пиломатериалов в Брянской области за 2004-2007 гг. с помощью аналитических показателей динамического ряда (цепным и базисным способом).

Постройте график производства пиломатериалов в Брянской области за 2004-2007 гг.

Задача 6.6.

Используя данные задачи 6.5., рассчитайте среднегодовое производство пиломатериалов в Брянской области за 2004-2007 гг.

Задача 6.7.

Используя данные задачи 6.5., определите значение среднего абсолютного прироста производство пиломатериалов в Брянской области.

Задача 6.8.

Используя данные задачи 6.5., определите средний темп роста производства пиломатериалов в Брянской области за 2004-2007 гг.

Задача 6.9.

Остатки вкладов населения в банках в I квартале приведены в табл.6.6.

Таблица 6.6 – Остатки вкладов населения, млрд. руб.

Показатель	на 1.01	на 1.02	на 1.03	на 1.04	на 1.05	на 1.06	на 1.07
Остатки вкладов	1416,3	1511,9	1611,6	1661,0	1740,5	1830,5	1928,0

Определите среднемесячный размер остатков вкладов населения в банках за первое полугодие.

Задача 6.10.

Имеются следующие данные о перевозке грузов железнодорожным транспортом в регионе по месяцам 2008 г., млн т:

Январь – 7,8	Июль – 9,3
Февраль – 8,2	Август – 9,9
Март -9,5	Сентябрь – 9,5
Апрель – 9,1	Октябрь – 9,9
Май – 9,5	Ноябрь – 9,7
Июнь – 9,0	Декабрь – 9,8

Преобразуйте исходные данные путем укрупнения периода времени (квартал). Нанесите полученные квартальные уровни на график. Сделайте выводы о характере общей тенденции изучаемого явления.

Задача 6.11.

Рассмотрите применение метода скользящей средней на основании данных задачи 8.10. Нанесите полученные при сглаживании данные на график. Сделайте выводы о характере общей тенденции изучаемого явления.

Задача 6.12.

Рассмотрите применение метода аналитического выравнивания по прямой для выражения общей тенденции на примере данных о перевозке грузов железнодорожным транспортом в регионе по месяцам 2008 г. (см. задачу 6.10.). Изобразите графически фактические уровни динамики и уровни, полученные при аналитическом выравнивании.

Сделайте выводы.

Задача 6.13.

Имеются следующие данные (табл. 6.7) о распределении браков.

Таблица 6.7 - Распределение браков, заключенных населением региона по месяцам 2006-2008 гг.

Месяц	Год			Месяц	Год
	2006	2007	2008		2006	2007	2008
Январь	3571	3450	3192	Июль	6346	6640	7620
Февраль	5325	5794	4598	Август	10691	10714	8232
Март	5504	4354	1779	Сентябрь	7013	7132	6668
Апрель	2474	2478	5747	Октябрь	5917	6498	6480
Май	1879	2755	1979	Ноябрь	7816	9495	6261
Июнь	7503	6712	5380	декабрь	2583	3883	2379

Для анализа внутригодовой динамики заключения населением браков определите индексы сезонности методом постоянной средней. Изобразите графически сезонную волну заключения населения браков по месяцам года. Сделайте выводы.

Контрольные вопросы

1. Какое значение имеют ряды динамики в статистической работе?

2. Какие существуют виды рядов динамики и в чем состоят их особенности?

3. Какова методика расчета средних уровней для периодических и моментных рядов динамики?

4. Какие существуют показатели анализа рядов динамики и порядок их вычисления?

5. Каковы приемы проявления тенденции развития динамических рядов и их значение в анализе?

6. Что является составными элементами ряда динамики?

7. Допускается ли суммирование уровней моментного ряда?

8. Что является важнейшим условием правильности построения ряда динамики?

9. Какие причины вызывают несопоставимость уровней ряда динамики ?

10. Как называется разность между последующим и предыдущим уровнями ряда?

11. Как называется отношение последующего уровня ряда к предыдущему?

12. Что является в общем случае компонентами ряда динамики?

13. Как называется модель, в которой компоненты ряда суммируются?

14. Как называется модель, в которой компоненты ряда умножаются?

15. Какая тенденция может наблюдаться в социально - экономических рядах?

16. Как называется тенденция изменения связи между отдельными уровнями ряда ?

17. Для чего предназначен метод Фостера – Стюарта?

18. Для чего предназначен метод простой скользящей средней?

19. Какие уравнения используются для отображения основной тенденции ряда динамики?

20. С помощью чего могут быть описаны сезонные колебания в ряду динамики?

Практическая работа №7

Исчисление индексов количественных и качественных показателей

Цель работы: изучить основные виды индексов; задачи, решаемые с помощью индексного метода; методологические принципы построения экономических индексов, индексных систем и мультипликативных индексных моделей; взаимосвязи между экономическими индексами.Напучиться подбирать форму и вид индекса, соответствующий исходным данным и задачам исследования; определять индивидуальные и сводные индексы в различных формах; строить индексные модели и интерпретировать результаты проводимого анализа.

Индекс – это относительная величина, показывающая, во сколько раз уровень изучаемого явления в данных условиях отличается от уровня того же явления в других условиях.

В статистике для обозначения индексируемой величины применяется соответствующая символика:

- объем выпуска – q;

- цена – р;

- затраты времени на единицу продукции (трудоемкость) – t;

- выработка продукции в единицу рабочего времени – w;

- заработная плата – f;

- себестоимость – z;

- фондоотдача – Н;

- объем основных производственных фондов – Ф;

- численность работающих –T;

- товарооборот – Q;

- общие затраты (расходы) на производство – С;

- общий фонд оплаты труда – F.

Чтобы различать к какому периоду относится индексируемая величина, принято возле соответствующего символа ставить знаки: 1 – для отчетного периода; 0 – для периодов, с которыми сравниваются отчетные показатели.

Относительная величина, получаемая при сравнении уровней, называется индивидуальным индексом, если исследователь не интересуется структурой изучаемого явления и количественную оценку уровня в данных условиях сравнивает с такой же конкретной величиной уровня этого явления в других условиях.

Если известно, что изучаемое явление неоднородно и сравнение уровней можно провести только после приведения их к общей мере, экономический анализ выполняют посредством так называемых общих (сводных) индексов.

Основные элементы общих индексов:

- индексируемая величина (признак, значение которого является объектом изучения);

- коэффициент соизмерения (весы). С его помощью переводятся в сопоставимый вид разнообразные элементы.

Наиболее типичным общим индексом количественных показателей является индекс физического объема.

Влияние на прирост товарооборота изменения количества проданных товаров отражается агрегатным индексом физического объема I_q , который строится также в предположении первичности изменения количественных показателей (q) и вторичности влияния качественных (р):

Рассчитанный по данной формуле индекс физического объема продукции показывает, во сколько раз изменился физический объем продукции или сколько процентов составляет его уменьшение (рост) в текущем периоде по сравнению с базисным.

Разность между числителем и знаменателем индекса свидетельствует об абсолютном росте или абсолютном уменьшение стоимости выпущенных товаров в текущем периоде по сравнению с базисным периодом в сопоставимых ценах на уровне базисного периода.

Индексы качественных показателей представлены следующими индексами:

Индексы цен

В международной статистической практике в настоящее время наиболее широко применяются формулы индексов цен Ласпейреса (с базисными весами), Пааше (с текущими весами) и Фишера.

В 1871 г. немецким экономистом Е. Ласпейресом предложен индекс цен Ласпейреса, где в качестве соизмерителя используется объем продукции по разновидности в базисном периоде q₀. Индекс Ласпейреса рассчитывается по формуле:

Индекс цен Пааше предложен в 1874 г. немецким экономистом Г. Пааше. В индексе в качестве соизмерителя используется объем продукции соответствующего вида в текущем периоде q₁. Индекс Пааше рассчитывается по формуле:

Учитывая имеющееся несоответствие между индексами Паше и Ласпейреса, И.Фишером в международном сопоставлении предложен «идеальный индекс» (индекс Фишера), как среднегеометрическая величина из двух вышеупомянутых индексов: .

Индекс себестоимости продукции рассчитывается по формуле:

Рассчитанный по данной формуле индекс себестоимости продукции показывает, во сколько раз уменьшился (увеличился) в среднем уровень себестоимости продукции, произведенную в текущем периоде, или сколько процентов составляет его уменьшение (рост) в текущем периоде по сравнению с базисным.

Разность между числителем и знаменателем индекса характеризует экономию (-) или перерасход (+) от изменения себестоимости единицы продукции.

Индекс производительности труда по расходам на единицу продукции рассчитывается по формуле:

В отличие от приведенных выше формул других агрегатных индексов, в этом индексе базисная величина индексируемого показателя (t₀) находится в числителе, а текущая величина (t₁) – в знаменателе. Это происходит потому, что затраты труда на единицу продукции и производительность труда связаны обратной зависимостью (w = 1/t).

Рассчитанный по данной формуле индекс производительности труда показывает, во сколько раз возрос (уменьшился) в среднем общий уровень трудоемкости текущего (отчетного) периода по сравнению с базисным.

Разность между числителем и знаменателем индекса показывает возрастание (+) или уменьшение (-) трудоемкости базисного периода на всю продукцию по сравнению с текущим.

Приведем формулы расчета некоторых наиболее употребительных агрегатных индексов.

1) В форме мультипликативной индексной модели динамика товарооборота будет выражаться соотношениями

где

Если принимается предположение об очередности влияния факторов – сначала q, а затем р, то общий прирост товарооборота будет распределяться по факторам следующим образом:

Если же принимается предположение об обратной последовательности влияния факторов – сначала р, затем q, то меняются и формулы разложения прироста и формулы расчета индексов I_q и I_p . Тогда

где

2) Индекс изменения общей суммы затрат на производство продукции в зависимости от объема производства (q) и затрат на единицу (z):

3) Индекс изменения общего фонда оплаты труда в связи с изменением общей численности работающих (Т) и заработной платы (f):

4) Индекс изменения объема продукции в связи с изменением численности работающих (Т) и уровня их выработки (w):

5) Индекс изменения объема продукции в связи с изменением объема основных производственных фондов (Ф) и показателя эффективности их использования – фондоотдачи (Н):

Существует две формы средневзвешенных индексов: среднеарифметическая и среднегармоническая. Как правило, средний арифметический индекс применяется при индексации количественных показателей (например, физического объема продукции), а средний гармонический – при индексации качественных показателей (например, цен).

Например, необходимо вычислить общий индекс физического объема продукции I_q , когда по исходным данным известны индивидуальные индексы физического объема ( ) и стоимость продукции каждого вида за базисный период ( ). Тогда общий индекс физического объема продукции можно определить как среднюю арифметическую взвешенную из индивидуальных индексов. Для этого заменяем неизвестное количество продукции отчетного периода ( ) произведением . Тогда общий индекс физического объема продукции приобретет вид:

Если индексируемая величина выражается через индивидуальный индекс в знаменателе, то индекс имеет название среднего гармонического индекса.

Например, известны индивидуальные индексы цен ( ) и стоимость каждого вида продукции за текущий (отчетный) период ( ), но неизвестны данные о цене единицы продукции за базисный период ( ). Чтобы найти средний гармонический индекс цен, цену базисного периода ( ) заменяем тождественным ей соотношением . Вследствие этого индекс цен будет иметь вид:

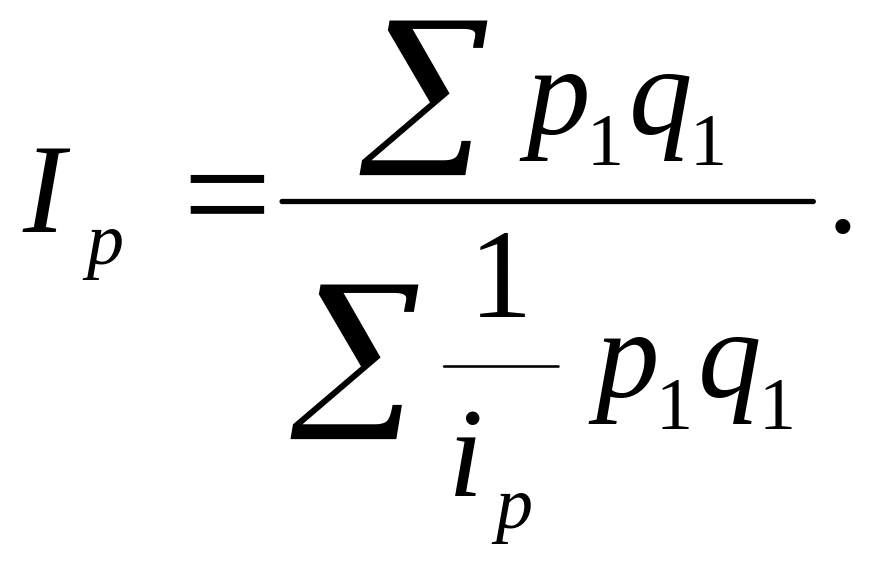
Так как на динамику средней влияют не только изменения осредняемого признака, но и изменения состава рассматриваемой совокупности, влияние каждого из этих факторов оценивается посредством общих индексов средних величин. Такие индексы образуют индексную систему, которая для качественных показателей состоит из трех элементов: индексов переменного состава ; индексов фиксированного (постоянного) состава ; индексов структурных сдвигов , где х – вид рассматриваемого признака (цена, себестоимость, производительность труда и т.п.).

Индекс переменного состава показывает относительное изменение рассматриваемого среднего уровня признака в целом за счет двух факторов – изменения индексируемого признака и изменения в структуре совокупности:

,

где - средние признаки соответственно в текущем и базисном периодах; - веса признака в сопоставимых периодах.

Для разных качественных показателей индекс переменного состава можно записать в виде следующих отношений:

1. Индекс себестоимости переменного состава: .

2. Индекс цен переменного состава: .

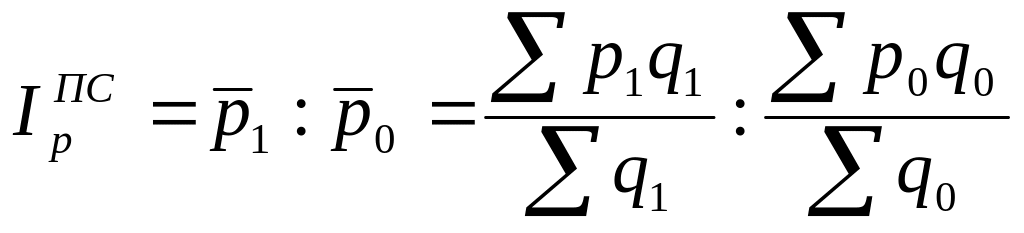3. Индекс производительности труда переменного состава:

Индекс фиксированного (постоянного) состава характеризует изменение среднего уровня за счет изменения только индексируемой величины при той же структуре совокупности (соизмерители неизменны):

.

Индекс структурных сдвигов показывает изменение среднего уровня показателя за счет изменений в структуре совокупности при неизменном значении признака:

Формулы для средних индексов подчиняются принципу взаимозависимости, который обеспечивает их сведение в индексную систему: . С использованием этой формулы по двум известным индексам можно рассчитать третий.

На основе вышеприведенных формул можно рассчитать абсолютное изменение среднего уровня вторичного признака за счет отдельных факторов – самого усредняемого признака и структуры : где

Влияние структурных сдвигов на изменение среднего уровня изучаемого явления особенно заметно при сравнениях за длительные периоды времени и в условиях существенных изменений в структуре социально-экономических процессов. В связи с этим исключение воздействия структурного фактора при анализе изменений средних значений признаков как показателей основной тенденции – это необходимое условие для получения реалистичной оценки и правильных выводов на основе индексного анализа различных сложных явлений.

В зависимости от выбора базы сравнения коэффициенты роста в рядах динамики могут рассчитываться либо с одной и той же базой сравнения, либо с переменной базой сравнения. Ряд коэффициентов роста (ряд индексов) с постоянной базой сравнения называется базисными индексами. Ряд же индексов, каждый из которых рассчитан по отношению к предыдущему периоду, называется цепными индексами. Между этими индексами существует определенная зависимость, позволяющая переходить от одних индексов к другим, например: Имеются данные за ряд периодов о каком-либо единичном показателе.

период	I	II	III	IV	V
уровень	у1	у2	у3	у4	у5

Принимаем за базу сравнения у₁, тогда базисные индексы для соответствующих периодов равны:

Цепные индексы записываются так:

Следовательно:

Произведение цепных индексов дает базисный индекс.

Отношение двух базисных индексов равно цепному индексу:

Упражнения и задачи

Задача 7.1

Имеются следующие данные (табл. 7.1) о производстве хлеба и хлебобулочных изделий предприятиями Брянской области, тыс. тонн:

Таблица 7.1 - Производство хлеба и хлебобулочных изделий предприятиями Брянской области

	1995	1999	2000	2001	2002	2003	2004	2005	2006	2007
Хлеб и хлебобулочные изделия	140,6	131,6	121,4	117,8	118,3	108,8	101,4	98,4	95,1	90,9

Определите индивидуальные индексы объема продукции: 1) цепным способом; 2) базисным способом, приняв за базу сравнения 1995 год; 3) выполните проверку расчета базисных индексов.

Задача 7.2

Имеются следующие данные (табл. 7.2):

Таблица 7.2 – Исходные данные

Виды изделия	Себестоимость 1 шт., руб.		Произведено, тыс. шт.		Индивидуальные индексы
	базисный период	отчетный период	базисный период	отчетный период	базисный период	отчетный период
А	132	?	1.2	1.31	0.92	?
Б	240	246	?	3.0	?	0.71
В	?	310	0.72	?	0.99	2.92

Определите: а) недостающие показатели в таблице; б) сводные индексы цен физического объема продукции (взвешенные по себестоимости) и затрат на производство.

Задача 7.3

Определите, как изменились в среднем отпускные цены на продукцию, если количество произведенной продукции в отчетном периоде по сравнению с базисным увеличилось на 8,0%, а общая стоимость продукции уменьшилась на 5,0%.

Задача 7.4

Имеются данные (табл. 7.3) о реализации помидоров магазином:

Таблица 7.3 – Исходные данные

Месяц	Цена за 1 кг, руб.	Продано, кг.
Июнь	45,0	700
Сентябрь	18,0	4500
Октябрь	35,0	2800

Определите цепные и базисные индексы цен, физического объема продажи и товарооборота, покажите взаимосвязь между ними.

Задача 7.5

Имеются данные (табл. 7.4) о продаже сельскохозяйственной продукции на рынке города:

Таблица 7.4 – Исходные данные

Товары	Продано за период, т		Средняя цена за 1 кг в течение периода, д.е.
	базисный период	отчетный период	базисный период	отчетный период
Картофель	800	950	1,00	4,20
Морковь	90	100	1,30	5,50
Свёкла	95	120	1,20	5,30
Капуста	20	15	0,80	4,60
Лук	30	35	1,50	8,00

Определите: 1) агрегатные индексы физического объема продукции, цен, стоимости (товарооборота); 2) абсолютный прирост (уменьшение) стоимости проданных товаров в результате изменения цен в текущем периоде.

Задача 7.6

Имеются данные (табл. 7.5) об объеме произведенной продукции и ее себестоимости на предприятии.

Таблица 7.5 – Исходные данные

Продукция	Объем произведенной продукции, тыс. шт.		Себестоимость продукции, д.е.
	базисный период	отчетный период	базисный период	отчетный период
А	3,1	3,3	1,1	1,2
Б	5,2	5,8	0,9	0,8

Определите: 1) индивидуальные индексы и агрегатные индексы физического объема продукции, себестоимости, расходов на производство продукции; 2) экономический эффект от снижения себестоимости продукции.

Задача 7.7

Имеются данные (табл.7.6) по сельскохозяйственным предприятиям о реализованной продукции в базисном периоде и изменениям в объеме продукции в текущем периоде:

Таблица 7.6 – Исходные данные

Продукция	Стоимость продукции в базисном периоде, тыс. д.е.	Изменение объема продукции в текущем периоде по сравнению с базисным
Зерно	310	+11%
Картофель	450	-3%
Овощи	102	Без изменений
Всего	862	х

Необходимо определить общий индекс физического объема продукции.

Задача 7.8

Имеются данные (табл. 7.7) о реализации продукции торговым предприятием:

Таблица 7.7 – Исходные данные

Товары	Объем потребления отчетного периода, тыс.д.е.	Индексы цен ip
Мясопродукты	315,0	1,05
Молочные продукты	26,5	0,95
Хлебопродукты	32,8	0,98
Всего	374,3	х

Определите общий индекс цен.

Задача 7.9

Имеются исходные данные (табл. 7.8) о количестве, ценах и стоимости реализованной продукции:

Таблица 7.8 – Исходные данные

Виды продукции	Количество реализованной продукции, тыс.ед.		Цена единицы продукции, руб.		Стоимость реализованной продукции, тыс.руб.
	q0	q1	p0	p1	q0 p0	q1 p0	q1 p1
А	100	130	20	15	2000	2600	1950
Б	150	160	12	13	1800	1920	2080
В	200	250	8	8	1600	2000	2000
Итого	х	х	х	х	5400	6520	6030

Определите: 1) в относительном и абсолютном выражении изменение стоимости реализованной продукции в отчетном периоде по сравнению с базисным периодом; 2) в какой мере это изменение вызвано изменением: а) количества реализованной продукции; б) цен разнородной продукции.

Задача 7.10

На основании данных задачи 7.9 определите:

1. индивидуальные индексы количества продукции;

2. индивидуальные индексы изменения цен;

3. средний взвешенный индекс количества продукции;

4. средневзвешенный индекс цен.

Задача 7.11

Имеются данные (табл. 7.9) о количестве, ценах, себестоимости и массе прибыли.

Таблица 7.9 – Исходные данные

Вид продукции	Количество, тыс.шт.		Цена ед. продукции, руб.		Себестоимость ед. продукции, руб.
	q0	q1	p0	p1	z0	z1
А	100	180	40	42	38	41
Б	50	100	10	9	9	7
В	10	40	8	6	10	5

Определите:

1. изменение прибыли в отчетном периоде по сравнению с базисным в относительном и абсолютном выражении;

2. изменение прибыли за счет изменения: а) количества продукции (физического объема); б) структуры реализованной продукции; в) цен реализованной продукции; г) себестоимости продукции.

3. Установление взаимосвязи в относительном и абсолютном выражении.

Задача 7.12

Имеются данные (табл. 7.10) о численности работников и фонде заработной платы предприятия:

Таблица 7.10 – Исходные данные

№ цеха	Численность работников		Фонд заработной платы, тыс.руб.
	базисный период Т0	отчетный период Т1	базисный период Т0f0	отчетный период Т1f1
1	200	230	2200	2250
2	350	340	2290	2519
3	250	260	1809	2900
Итого	800	830	7129	7669

Определите:

1. среднюю заработную плату в целом по предприятию в базисном и отчетном периодах;

2. изменение средней заработной платы в отчетном периоде по сравнению с базисным в относительном и абсолютном выражении;

3. в какой мере оказало влияние на изменение средней заработной платы: а) изменение структуры работников; б) изменение заработной платы в отдельных цехах.

Задача 7.13

Как в среднем изменились цены на молочную продукцию, если известно, что объем реализации за период увеличился на 15%, а товарооборот по этой группе товаров увеличился на 21%.

Задача 7.14

Трудоемкость одного изделия в отчетном периоде снизилась на 2,5%, а объем произведенной за этот период продукции увеличился на 3,2%. Как изменились при этом затраты времени на производство этой продукции.

Контрольные вопросы

1. Назовите задачи, которые решают с помощью индексов.

2. Перечислите основные элементы индексов.

3. Какие индексы бывают по форме построения?

4. Какие индексы бывают по базе сравнения?

5. Что означает в теории индексов параметр q?

6. Что означает в теории индексов параметр р?

7. Как исчисляют агрегатные и средние из индивидуальных индексы цен?

8. Какие формы средних используются при расчете средних индексов?

9. Где нашли наибольшее применение средние индексы?

10. Как определить агрегатный индекс цен по формуле Пааше?

11. Как определить агрегатный индекс цен по формуле Ласпейреса?

12. Как определить индекс товарооборота?

13. Что выражает индекс переменного состава?

14. Что выражает индекс постоянного состава?

15. Что характеризует индекс физического объема продукции?

16. Расскажите о взаимосвязи между индексами переменного, постоянного состава и структуры.

Практическая работа №8

Исследование связи между явлениями на основе корреляционного анализа. Расчет коэффициента корреляции и корреляционного отношения.

Построение уравнений регрессии

Цель работы: изучить классификацию взаимосвязей социально-экономических явлений по различным признакам; теоретические основы и последовательность моделирования взаимосвязей; коэффициенты, оценивающие силу и направление взаимосвязи, величину влияния одних факторов на другие; методику оценки точности результатов моделирования взаимосвязи; методы определения взаимосвязи между качественными признаками. Научиться обоснованно выбирать и строить модели для анализа взаимосвязей с использованием компьютерных программ; определять параметры линейных и нелинейных уравнений регрессии, рассчитывать показатели силы взаимосвязи, абсолютного и относительного влияния одних факторов на другие; интерпретировать результаты расчётов и определять значимость показателей взаимосвязи; рассчитывать ранговые и другие непараметрические коэффициенты взаимосвязи.

Формы проявления взаимосвязей весьма разнообразны. В качестве двух самых общих их видов выделяют функциональную (полную) и стохастическую (неполную, статистическую) связи. Стохастическая связь, когда каждому отдельному значению факторного признака х отвечает определенное множество значений результативного признака у.

Разновидностью стохастической связи является корреляционная зависимость, которая предопределяет корреляционную зависимость между признаками. При такой зависимости с изменением факторного признака х изменяются групповые средние результативного признака у и вместо условных распределений множеств значений признака у выступают средние значений этих распределений

Задачи собственно корреляционного анализа сводятся к измерению тесноты связи между варьирующими признаками, определению неизвестных причинных связей и оценке факторов, оказывающих наибольшее влияние на результативный признак. Задачи регрессионного анализа лежат в сфере установления формы зависимости, определения функции регрессии, использования уравнения для оценки неизвестных значений зависимой переменной.

Изучение корреляционной связи между признаками начинается с регрессионного анализа, который решает проблему установления формы связи, вида уравнения регрессии, определения параметров уравнения регрессии.

В регрессионном анализе различают уравнения парной (простой) и множественной (многофакторной) регрессии. Когда связь с результативным признаком у осуществляется с одним видом факторного признака х, то уравнение регрессии называется уравнением парной регрессии. Если результативный признак у связан с несколькими видами факторных признаков , то такая зависимость называется уравнением множественной регрессии.

Наиболее часто для характеристики корреляционной связи между признаками применяют такие виды уравнений парной регрессии, или корреляционных уравнений:

а) линейный

б) параболический

в) гиперболический

г) степенной и др.,

где а₀, а₁ – параметры уравнений регрессии, который подлежат определению.

Параметры в уравнениях регрессии определяются методом наименьших квадратов. Этот метод наилучшим образом отвечает корреляционной таблице и допускает нахождение таких значений параметра уравнения регрессии, при которых сумма квадратов отклонений табличных (фактических) значений результативного признака у от теоретических значений Y по линии регрессии была бы минимальной:

Функция S параметров уравнения регрессии будет минимальной тогда, когда выполняются необходимые условия нахождения экстремума этой функции – равенство нулю первых производных функции по разыскиваемым параметрам:

Из этих условий формируется система нормальных уравнений для нахождения параметров а₀ и а₁.

В случае линейного вида уравнения регрессии ( ), которое отвечает линейной зависимости между признаками, система нормальных уравнений записывается в виде:

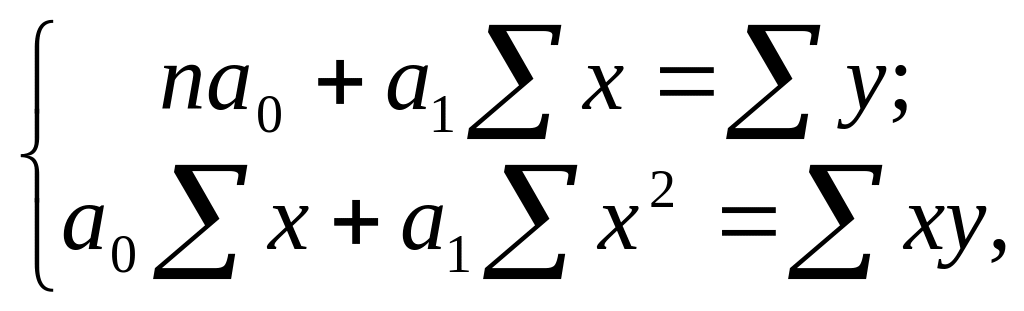
где n – количество единиц совокупности (то есть заданных пар значений х и у).

Решив эту систему, находим такие значения параметров:

или

; ,

где - средняя из произведения факторного признака на результативный; - средняя из суммы квадратов факторного признака; - квадрат средней из факторного признака.

Использовав уравнение регрессии, можно найти теоретическое значение Y для любого значения факторного признака х.

В уравнении регрессии параметр а₀ экономического смысла не имеет, а геометрически он отвечает значению ординаты линии регрессии Y при х = 0. Параметр а₁ называется коэффициентом регрессии и показывает изменение результативного признака Y при изменении факторного признака х на единицу; геометрически параметр а₁ отвечает углу наклона ( в радианах) прямой линии регрессии к горизонтали оси.

После выбора вида уравнения регрессии и нахождения его параметров выполняют второй этап КРА – корреляционный анализ, в рамках которого дают оценку тесноты и значимости связи.

В понятие «теснота связи» вкладывается оценка влияния факторного признака на результативный и установление адекватности теоретической зависимости между признаками по фактическим данным. Тесноту связи между признаками оценивают по средствам таких характеристик: коэффициент детерминации; коэффициент корреляции (корреляционное отношение) и др.

Коэффициент детерминации показывает, какая доля общей вариации результата, принятой за 1, формируется под влиянием данного фактора, а какая - за счет воздействия прочих причин. Он используется как при линейной, так и при нелинейной связи между признаками, и в случае парной регрессии рассчитывается по формуле:

Коэффициент детерминации принимает значения от 0 до 1. Понятно, что чем ближе коэффициент к 1, тем теснее выявленная зависимость и тем большую роль играет данный фактор в формировании изменений результата. При R²=0 отсутствует линейная связь между признаками.

Коэффициент корреляции (корреляционное отношение) показывает, насколько значимым является влияние признака х на Y. Коэффициент корреляции рассчитывается по формуле: .

Он находится в диапазоне ; чем более близок R к единице, тем теснее корреляционная связь между признаками.

В случае линейной связи между Y и х величина линейного коэффициента корреляции определяется по формулам:

;

.

Коэффициент корреляции принимает значения в интервале от -1 до + 1. Принято считать, что если  |r| < 0,30, то связь слабая; при  |r| = (0,3÷0,7) – средняя; при  |r| > 0,70 – сильная, или тесная. Когда  |r| = 1 – связь функциональная. Если же r принимает значение около 0, то это дает основание говорить об отсутствии линейной связи между Y и х.

Когда r>0 , то связь между признаками прямая, при r<0 – обратная.

После установления тесноты связи дают оценку значимости связи между признаками. Под термином «значимость связи» понимают оценку отклонения выборочных переменных от своих значений в генеральной совокупности посредством статистических критериев. Оценку значимости связи осуществляют с использованием F-критерия Фишера и t-критерия Стьюдента.

Для парной регрессии (линейной и нелинейной) F-критерий Фишера рассчитывается по формуле:

,

где - число степеней свободы числителя и знаменателя зависимости.

Теоретическое значение F сравнивают с табличным (критическим) значением F_табл.. Если F> F_табл, то выборочная совокупность и связь между признаками является значимой.

Для парной линейной регрессии при r=R расчетные критерии t-критерия Стьюдента вычисляются по формуле:

, где (n-2) – число степеней свободы.

Критерий Стьюдента, рассчитанный по данной формуле, дает оценку значимости коэффициента корреляции R и существенности связи между признаками. Рассчитанное теоретическое значение t-критерия Стьюдента сравнивают с табличным t_табл, если t>t_табл , то линейный коэффициент корреляции является значимым при характеристики генеральной совокупности.

Использование регрессионного и корреляционного анализа требует, чтобы все признаки были количественно измеренными. Методы КРА, основанные на использовании количественных параметров распределения (средние величины, дисперсия), называют параметрическими методами.

Вместе с тем в статистике, особенно при проведении социологических исследований, возникает потребность оценки тесноты связи между качественными (атрибутивными) признаками. Проблему оценки тесноты связи между атрибутивными признаками решают непараметрические методы. Сфера их использования значительно шире в сравнении с параметрическими методами, потому что не требует использования условия нормального распределения результативной переменной, не ставится задача представления зависимости между атрибутивными признаками соответствующим уравнением. Здесь речь идет только о наличии установления связи и измерения его тесноты.

Относительной мерой тесноты стохастической связи между признаками служат также:

- коэффициент взаимной сопряженности Чупрова

;

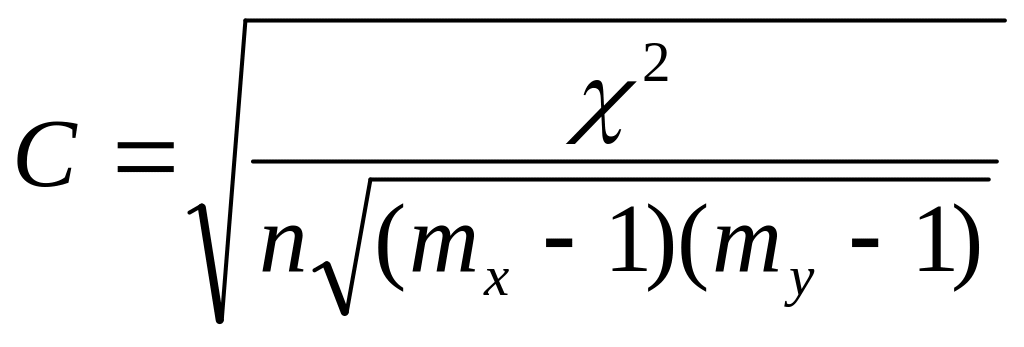- коэффициент взаимной сопряженности Крамера (при m_x m_y).

,

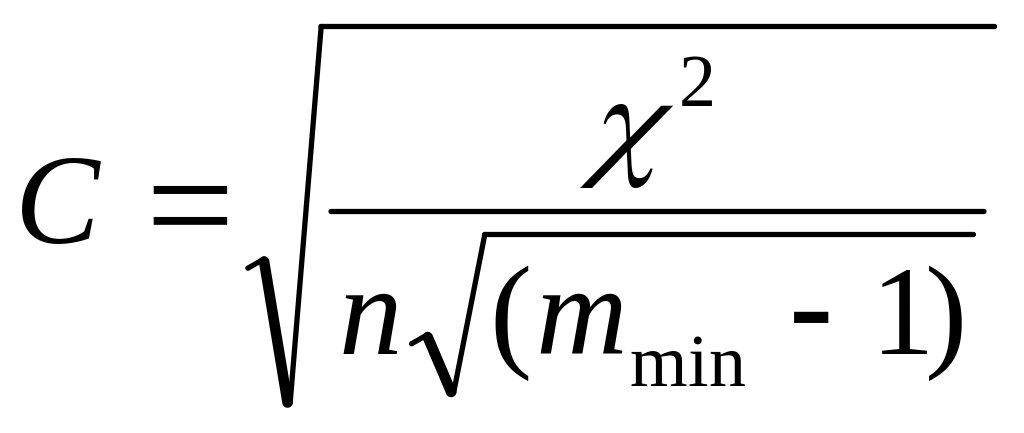где m_min – минимальное число групп (m_x или m_y).

Значение коэффициент С колеблется от 0 до 1 и теснота связи тем сильнее, чем более близко С к 1.

Достаточно часто в практике статистических исследований анализируются связи между альтернативными признаками, которые представлены группами с противоположными (взаимоисключающими) характеристиками. Тесноту связи в этом случае можно оценивать посредством коэффициента ассоциации Д.Юла и коэффициента контингенции К.Пирсона.

Для расчета указанных коэффициентов измерения тесноты связи между альтернативными признаками используется таблица взаимной сопряженности в виде корреляционной таблицы, которая носит название «четырехклеточной таблицы».

Таблица 8.1 - Таблица взаимной сопряженности

a	b	a+d
c	d	c+d
a+c	b+d	a+b+c+d

При использовании таблицы 10.1 с частотами a,b,c,d коэффициент ассоциации (К_а) вычисляется по формуле:

При К_а>0,3 между изучаемыми качественными признаками существует корреляционная связь.

В случаях, когда один из показателей четерехклеточной таблицы отсутствует, величина коэффициента ассоциации будет равняться единице, что дает завышенную оценку тесноты связи между признаками. В этом случае необходимо рассчитывать коэффициент контингенции (К_k):

Коэффициент контингенции находится в диапазоне от -1 к +1. Чем более близок K_k к (+1) или (-1), тем теснее связь между изучаемыми признаками. Коэффициент контингенции всегда меньше коэффициента ассоциации.

Для определения связи как между количественными, так и между качественными признаками при условии, что значения этих признаков упорядочены по степени уменьшения или увеличения (ранжированные), может быть использован коэффициент корреляции рангов Спирмена. Рангами называют числа натурального ряда, которые представляются в баллах по определенным критериям элементов совокупности. При этом ранжирование проводится по каждому признаку отдельно: первый ранг предоставляется наименьшему значению признака, последний – наибольшему. Количество рангов равняется объему совокупности. Преимуществом этого подхода является то, что при отсутствии требования нормального распределения ранговые оценки тесноты связи целесообразно использовать для совокупности небольшого объема.

Показатель ранговой корреляции – коэффициент корреляции рангов Спирмена – рассчитывается по формуле:

где - разность между рангами по одному и другому признаку ( );

n – количество единиц в ряду.

Если =0, то - существует тесная прямая связь. Если первому рангу по размеру одного признака соответствует последний ранг по размеру второго признака, второму рангу – предпоследний ранг второго признака и т.п., то и существует тесная обратная связь. Если значение близко к нулю, то связь слабая или ее вообще нет.

Упражнения и задачи

Задача 8.1

Рассчитайте параметры линейного уравнения парной регрессии, которое будет характеризовать зависимость между недельным розничным товарооборотом (д.е.) на душу населения и доходами населения (д.е.), и проведите анализ параметров регрессии по данным таблицы 8.2.

Таблица 8.2 – Исходные данные

Доходы населения	18	20	21	22	24	25	27	28	29	31
Розничный товарооборот	17	18	19	20	21	23	24	25	26	27

Задача 8.2

По данным задачи 8.1 оцените тесноту и значимость связи между признаками.

Задача 8.3

Оцените тесноту связи между атрибутивными признаками рабочих предприятия по данным таблицы 8.3.

Таблица 8.3 – Распределение мнений по оценке содержания работы

Работа	Мужчины	Женщины	Итого
Интересная	300 (а)	200 (b)	500 (a + b)
Неинтересная	129 (с)	251 (d)	380 (c + d)
Всего	429 (а + с)	451 (b + d)	880 ( a + b + c + d)

Задача 8.4

Требуется доказать, влияет ли увеличение дозы внесения минеральных удобрений на урожайность зерновых культур.

Результаты опыта приведены в таблице 8.4.

Таблица 8.4 – Результаты опыта

Варианты опыта по внесению удобрений, ц/га	Урожайность по повторностям, Y1
	I	II	III	IV	V	VI	гр
Контроль	18	18	14	17	19	16	17
1,5	15	21	18	19	19	16	18
2,0	22	20	19	19	23	17	20
2,5	20	25	19	21	23	18	21

Задача 8.5

20 явлений сгруппированы в четыре группы по 5 явлений в каждой группе. Общая сумма квадратов отклонений от общей средней равны 160. Средние значения изучаемого признака по группам равны: 17, 20, 21, 18. С помощью дисперсионного метода доказать, что различия между средними по группам не случайные, а вызваны влиянием изучаемого фактора. Табличное значение F-критерия с вероятностью p=0,95 равно F_табл=3,5.

Задача 8.6

По следующим данным (табл. 8.5) с помощью критерия при 5% уровне значимости проверьте гипотезу о том, что «наследственность» является фактором возникновения гипертонической болезни.

Оцените тесноту связи между заболеваемостью и наследственностью с помощью:

С – коэффициента взаимной сопряжённости Пирсона;

С’– нормированного коэффициента Пирсона;

Т – коэффициента взаимной сопряжённости Чупрова.

Таблица 8.5 – Исходные данные

Родители больны гипертонией	Обследовано на заводе «Электосигнал», чел.
	Всего	Больные гипертонией	Здоровые
Да	17	15	2
Нет	73	30	43
Итого	90	45	45

Задача 8.7

По ряду районов Закарпатья определены: среднесуточное количество йода в воде и пище и пораженность населения заболеванием щитовидной железы.

Номер района	Количество йода в воде и пище (усл.ед.)	Пораженность населения заболеванием щитовидной железы, %
1	201	0,2
2	178	0,6
3	155	1,1
4	154	0,8
5	126	2,5
6	81	4,4
7	71	16,9

Для оценки тесноты связи пораженности заболеванием щитовидной железы с количеством йода в воде и пище определите коэффициенты корреляции рангов Спирмена.

Контрольные вопросы

1. Почему возникает необходимость в установлении связи между признаками явлений?

2. Какие признаки называются факторными, результативными?

3. Какую связь между признаками называют функциональной? Приведите примеры?

4. Какую связь между признаками называют стохастической? Приведите примеры.

5. Какую связь между признаками называют корреляционной? Приведите примеры.

6. Что представляет собой уравнение регрессии?

7. Что представляет собой корреляционно-регрессионный анализ?

8. Суть регрессионного анализа.

9. Какие уравнения регрессии называют парными, а какие множественными?

10. Суть корреляционного анализа.

11. Какие виды уравнений парной регрессии наиболее распространены при характеристике социально-экономических явлений? Какие линии регрессии они описывают?

12. Приведите примеры использования линейной, параболической, гиперболической, степенной зависимости парной регрессии. Объясните структуру и вид зависимости.

13. Объясните понятие тесноты и значимости связи между признаками.

14. Характеристики тесноты связи: коэффициент детерминации; коэффициент корреляции.

15. Статистические критерии значимости связи между признаками: F-критерий Фишера; t-критерий Стьюдента.

16. Как оценивается теснота связи между атрибутивными признаками?

Список рекомендуемой литературы