Порядок выполнения работы №1

Для выполнения работы необходимо запустить программную среду MATHCAD и загрузить лабораторную работу 1 (\Laba1\4_1.mcd).

1. Просмотреть Лабораторную работу №1 от начала и до конца, для различных видов видеосигналов с базовыми данными амплитуды, периода, длительности, временного сдвига. По ходу просмотра необходимо обратить внимание на исходные данные, аналитические выражения, временные и частотные зависимости. Убедиться в том, что разным видам последовательностей соответствуют различные спектры амплитуд и фаз.

2. Получить от преподавателя вид последовательности для проведения исследования.

3. Для временной зависимости последовательности видеоимпульсов установить максимальное значение ординаты равной удвоенной амплитуде импульса. Интервалы времени необходимо установить равным предельным значениям, указанным на оси времени.

4. Для АЧС по оси ординат установить удвоенное значение ординаты, а по оси абсцисс предельные значения круговой частоты указанные на оси частот.

5. Для ФЧС на оси ординат установить значения фазы от (-4) до (+4), а по оси абсцисс предельное значение круговой частоты, указанное на оси частот.

6. Исследуем влияние амплитуды сигнала:

6.1. Увеличим амплитуду в два раза. При этом амплитуды гармоник в спектре амплитуд удвоились. Все остальные параметры АЧС и ФЧС остались неизменными.

6.2. Уменьшим исходную амплитуду сигнала в два раза. При этом амплитуды гармоник в спектре амплитуд уменьшились в два раза. Все остальные параметры АЧС и ФЧС остались неизменными.

6.3. Восстановим исходную амплитуду.

7. Исследуем влияние периода следования видеоимпульсов:

7.1 Увеличим период в два раза. При этом уменьшаются амплитуды гармоник и расстояния между гармониками, следовательно и основная частота .

7.2 Уменьшим исходный период в два раза. При этом увеличились амплитуды гармоник в два раза и в два раза увеличилась основная частота . Ширина спектра остается неизменной.

7.3 Восстановим исходный период.

8. Исследуем влияние длительности импульса периодической последовательности. Одновременно с изменением длительности необходимо изменять временной сдвиг .

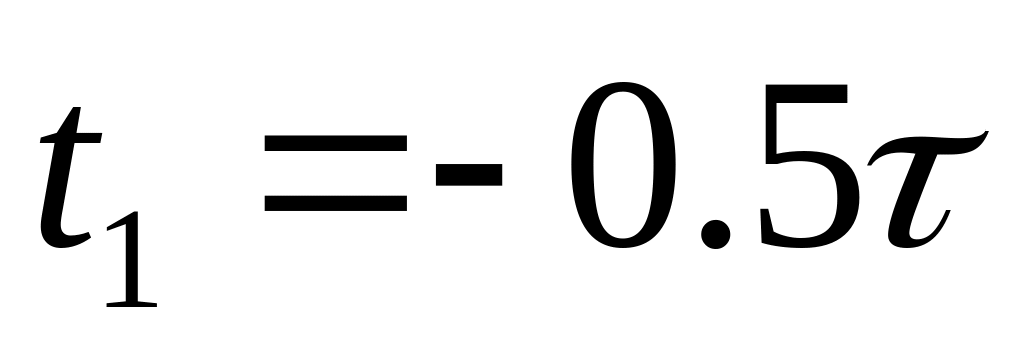8.1. Увеличим длительность импульса в два раза. При этом основная частота осталась неизменной, амплитуды гармоник увеличились в два раза и в два раза уменьшилась ширина спектра.

8.2. Уменьшим исходную длительность в два раза. При этом основная частота

осталась неизменной, амплитуды гармоник уменьшились в два раза и в два раза увеличилась ширина спектра.

8.3 Восстановим исходную длительность.

9. Исследуем влияние времени запаздывания середины длительности импульса 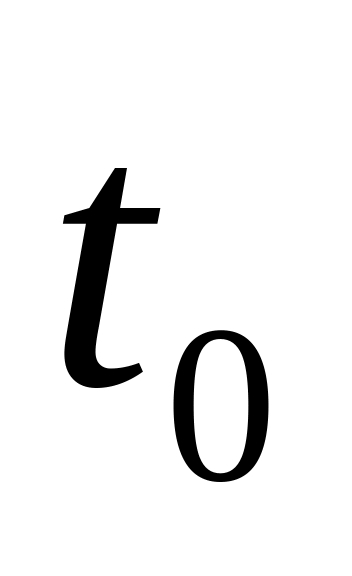относительно нуля:

9.1 Установить временной сдвиг ( ). Импульсы сдвинуться вправо (запаздывание). При этом АЧС останется неизменным, изменится ФЧС.

9.2 Установить временной сдвиг ( ). Импульсы сдвинутся влево (опережение). Изменится ФЧС, а АЧС остается неизменной.

9.3 Восстановим исходные данные ( ).

10. При исследовании спектра периодической последовательности ограниченного гармонического сигнала следует исследовать изменение амплитуды сигнала 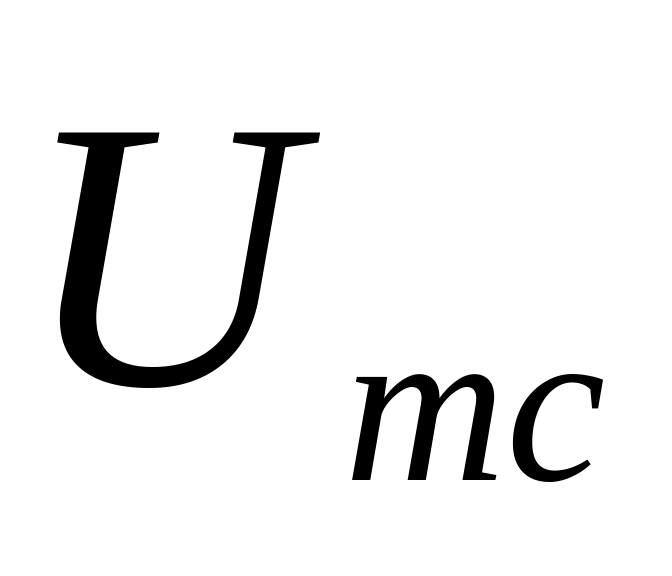, периода следования импульсов 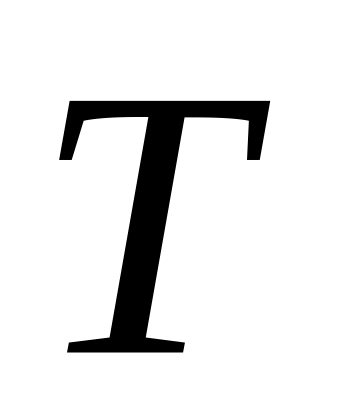и угла отсечки . При исследовании спектров от изменения угла отсечки, синхронно с изменением угла отсечки следует изменять амплитуду 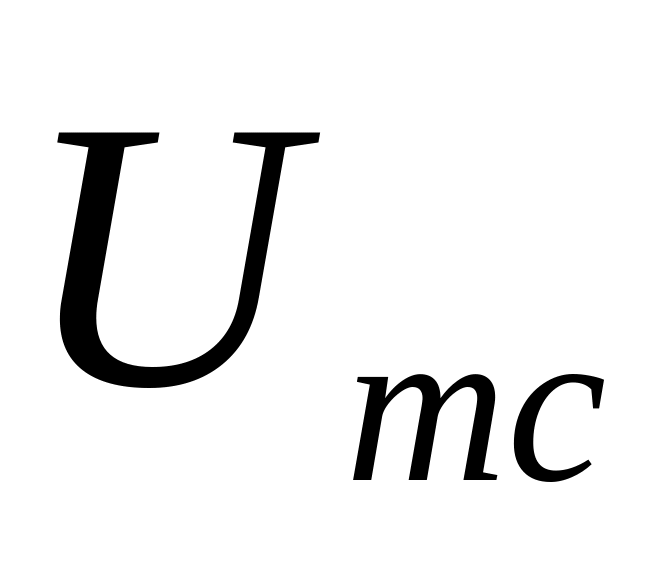для поддержания постоянной амплитуды импульсов периодической последовательности в соответствии с таблицей 1.1.

Таблица 1.1

, град	10	20	30	60	90	120	150	170	180
, В	650	165	75	20	10	6,5	5,3	5,05	5

11. По результатам проведенных исследований необходимо составить отчет, который должен содержать по каждому пункту исследований:

1. исходные данные;

2. временные зависимости;

3. частотные зависимости (АЧС и ФЧС). Если зависимость неизменна при изменении параметров, то ее необходимо приводить только для исходных данных;

4. выводы по работе.

Указание: масштабы по осям времени и частоты в процессе исследований должны оставаться неизменными. По осям ординат предельные значения должны быть постоянными.