26. Нормальный закон распределения непрерывной случайной величины. Нормальная кривая.

Нормальный закон распределения (закон Гаусса). Непрерывная случайная величина Х имеет нормальный закон распределения с параметрами   и  (обозначают  ), если ее плотность вероятности имеет вид:

, где   ,   .
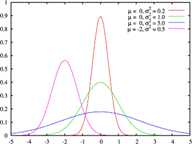
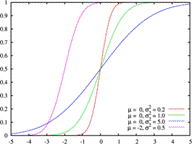
	Функция плотности  вероятности f(x)	Функция распределения F(x)
Рис.2. Нормальный закон распределения

Математическое ожидание характеризует центр рассеивания значений случайной величины и при изменении   кривая будет смещаться вдоль оси абсцисс (см. рис. 2 при   и при  ). Если же при неизменном математическом ожидании у случайной величины изменяется дисперсия, то кривая будет изменять свою форму, сжимаясь или растягиваясь (см. рис. 2 при  :  ;  ;  ). Таким образом, параметр   характеризует положение, а параметр  - форму кривой плотности вероятности.

Нормальный закон распределения случайной величины Х с параметрами   и   (обозначается N(0;1)) называется стандартным илинормированным, а соответствующая нормальная кривая – стандартной или нормированной.

Согласно определению функция плотности вероятности и функция распределения связаны между собой:

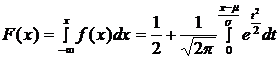 ,   где   .

27. Показательное распределение непрерывной случайной величины

Непрерывная случайная величина  имеет показательное распределение с параметром  > 0, если она принимает только неотрицательные значения, а ее плотность распределения p_ (x )и функция распределения F_ (x) имеют соответственно вид:

    ,  .

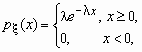
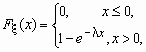
28. Статистическое распределение выборки

1. Статистическое дискретное распределение. Полигон.  Пусть из генеральной совокупности извлечена выборка, причем х₁ наблюдалось n₁ раз, х₂ – n₂ раз, х_k– n_k раз и ∑n_i=n - объем выборки. Наблюдаемые значения х₁ называют вариантами, а последовательность вариант, записанных в возрастающем порядке – вариационным рядом. Число наблюдений варианты называют частотой, а ее отношение к объему выборки - относительной частотой n_i/n=w_i

ОПРЕДЕЛЕНИЕ. Статистическим (эмпирическим) законом распределения выборки, или просто статистическим распределением выборки называют последовательность вариант х_i и соответствующих им частот n_i или относительных частот w_i.

Статистическое распределение выборки удобно представлять в форме таблицы распределения частот, называемой статистическим дискретным рядом распределения:

29. Гистограмма и полигон, как характеристики статистического распределения

ля наглядного представления вариационного ряда большое значение имеют его графические изображения. Графически вариационный ряд может быть изображен в виде полигона, гистограммы и кумуляты.

Полигон распределения (дословно — многоугольник распределения) строится в прямоугольной системе координат. Величина признака откладывается на оси абсцисс, частоты или относительные частоты — по оси ординат. Чаще всего полигоны применяются для изображения дискретных вариационных рядов, но их можно применять также для интервальных рядов. В этом случае на оси абсцисс откладываются точки, соответствующие серединам данных интервалов.

Гистограмма распределения строится аналогично полигону в прямоугольной системе координат. В отличие от полигона при построении гистограммы на оси абсцисс выбирают не точки, а отрезки, изображающие интервал, а вместо ординат, соответствующих частотам или относительным частотам отдельных вариант, строят прямоугольники с высотой, пропорциональной частотам или относительным частотам интервала. В случае интервалов различной длины гистограмма распределения строится, не по частотам или относительным частотам, а по плотности интервалов (абсолютной или относительной). При этом общая площадь гистограммы равна численности совокупности, если построение проводится по абсолютной плотности, или единице, если гистограмма построена по относительной плотности.

Если соединить прямыми линиями середины верхних сторон прямоугольников, то получим полигоны распределения.

Разбивая интервалы на несколько частей и исходя из того, что вся — площадь гистограммы должна остаться при этом неизменной, можно получить мелкоступенчатую гистограмму, которая при уменьшении величины интервала будет приближаться к плавной кривой, называемой кривой распределения.
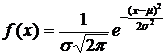