9. Следствия теоремы о базисном миноре.

Следствие 1. Строки матрицы образуют линейно-зависимую систему тогда и только тогда, когда ранг матрицы меньше количества строк.

Доказательство:

Пусть строки матрицы линейно-зависимы среди них есть хотя бы одна не базисная

.

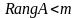Утверждение 2. Пусть среди столбцов есть линейно-зависимая подсистема. Тогда и вся система столбцов линейно-зависимая.

Доказательство:

Пусть для определенности - линейно-зависимая подсистема и , не все равные нулю.

.

(не все = 0).

являются линейно-зависимыми по определению.

(в доказательстве используем Следствие 1).

Следствие 2. Пусть . строка (столбец) образуют линейно-зависимую систему).

. Пусть строки (столбцы) образуют линейно-зависимую систему, тогда в силу свойств определителей .

. Пусть 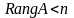хотя бы одна строка (столбец) может быть выражена через базисные столбцы линейным образом они вместе с базисными строками образуют линейно-зависимую систему и в силу утверждения все строки матрицы образуют линейно-зависимую систему.

С ледствие 3. Пусть система столбцов содержит столбцов: , - высота столбцов.

Т огда система столбцов линейно зависима. Рассмотрим матрицу:

хотя бы один из столбцов является небазисным

система линейно-зависимая.

Следствие 4. (теорема о ранге матрицы).

Максимальное число линейно-независимых строк равно максимальному числу линейно-независимых столбцов и равно .

10. Следствия теоремы о базисном миноре.

Следствие 1. Строки матрицы образуют линейно-зависимую систему тогда и только тогда, когда ранг матрицы меньше количества строк.

Доказательство:

Пусть строки матрицы линейно-зависимы среди них есть хотя бы одна не базисная

.

Утверждение 2. Пусть среди столбцов есть линейно-зависимая подсистема. Тогда и вся система столбцов линейно-зависимая.

Доказательство:

Пусть для определенности - линейно-зависимая подсистема и , не все равные нулю.

.

(не все = 0).

являются линейно-зависимыми по определению.

(в доказательстве используем Следствие 1).

Следствие 2. Пусть . строка (столбец) образуют линейно-зависимую систему).

. Пусть строки (столбцы) образуют линейно-зависимую систему, тогда в силу свойств определителей .

. Пусть хотя бы одна строка (столбец) может быть выражена через базисные столбцы линейным образом они вместе с базисными строками образуют линейно-зависимую систему и в силу утверждения все строки матрицы образуют линейно-зависимую систему.

С ледствие 3. Пусть система столбцов содержит столбцов: , - высота столбцов.

Т огда система столбцов линейно зависима. Рассмотрим матрицу:

хотя бы один из столбцов является небазисным

система линейно-зависимая.

Следствие 4. (теорема о ранге матрицы).

Максимальное число линейно-независимых строк равно максимальному числу линейно-независимых столбцов и равно .

Доказательство:

Пусть . Докажем для столбцов существование линейно-независимых базисных столбцов. Необходимо доказать, что любая система из столбцов является линейно-зависимой. Пусть для определенности базисными будут являться первые столбцов. Выделим произвольную систему из столбцов: . Составим из этих столбцов матрицу:

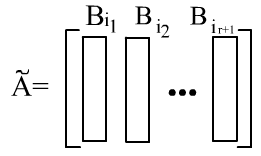
Очевидно, что миноры матрицы являются одновременно минорами исходной матрицы. все миноры матрицы -го порядка равны нулю среди столбцов матрицы есть хотя бы один небазисный система является линейно-зависимой.

Определение: Элементарными преобразованиями строк называется:

1). Сложение строк

2). Умножение строки на число

3). Перестановка строк.