38. Матрица линейного оператора.

Пусть - базис в

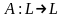- Л.О.

Определение. - называется матрицей оператора в базисе .

Замечание.

Вообще говоря матрица оператора зависит от базиса.

- в любом базисе ( - тождественный оператор)

Примеры.

1). Выписать матрицу поворота вокруг на против часовой стрелки. .

2).

3). - многочлены степени не выше 3. Матрица оператора в базисе .

П.3. Вычисление координат образа вектора.

,

- базис в .

Пусть - матрица Л.О. в базисе . Пусть также .

- столбцы координат элементов в базисе .

Связь

Теорема.

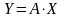
Доказательство.

,

, где

39. Сумма операторов. Произведение л.О. На число. Произведение л. Операторов.

Определение 2. Пусть - линейные операторы.

Пусть

Тогда говорят, что оператор является суммой Л.О. и

Определение 3.

Пусть …. , где - действительное число. Тогда говорят, что оператор является произведением оператора на число .

Определение 4.

Пусть . Тогда говорят, что оператор является произведением Л.О. и

Теорема 1.

- матрица операторов.

Доказательство.

=

Замечание.

- матрица оператора заполняется по столбцам.

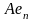
Теорема 2.

Пусть , тогда С , где С - в одном и том же базисе.

Доказать самостоятельно

Теорема 3.

Пусть , тогда С

Доказательство

С

40. Преобразование матрицы оператора при переходе к новому базису.

,

- базис в

Пусть С - матрица перехода

Доказательство.

Теорема 2.

Доказательство.

Замечание.

Говорят, что определитель матрицы оператора является инвариантом по отношению к изменению базиса.

41. Собственные числа и собственные векторы л.О.

,

Определение. Действительное число называется собственным числом Л.О. , а вектор - соответствующим вектором, если

Примеры.

1.

Всё линейное пространство состоит из собственных векторов.

2 . - проектор на плоскость

Множество собственных векторов

,

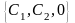Утверждение. Собственный вектор не может соответствовать двум различным собственным числам.

Доказательство.

Пусть

Определение.

Матрица называется характеристической матрицей Л.О.

- характеристическим многочленом Л.О.

= 0 характеристическими числами Л.О.

Утверждение. Характеристические числа не зависят от базиса.

Доказательство

Докажем, что характеристические числа не зависят от базиса.

Пусть есть базисы и , а также известна матрица перехода С . Тогда

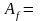С С

Выпишем характеристический многочлен в новом базисе.

( С С ) = ( С С ) =

С С = .

Характеристический многочлен не изменяется характеристические числа не изменяются.

Как вычислить собственные вектора и собственные числа ?

Теорема. , (матрица оператора в базисе)

является собственным вектором оператора соответствующего собственного числа

1). - действительный корень характеристического уравнения

2). - нетривиальное решение системы

- столбец координат в характеристическом базисе .

Доказательство: - собственный вектор оператора , соответствующего собственному числу

, , - вещественное число.

, , - вещественное число.

, , - вещественное число.

1). (чтобы существовало нетривиальное решение )

2). , - вещественное число.