1. Матрицы и действия над ними. Типы матриц.

Определение 1. Матрицей порядка назовем прямоугольную таблицу из чисел, состоящую из строк и столбцов.

Числа называются элементами матрицы . Элемент стоит на пересечении -той троки и -того столбца.

{ , }

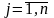Типы матриц.

1). Если , то матрица называется квадратной.

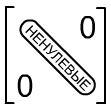
2). - «нуль-матрица».

3). Главная диагональ:

Если все элементы, лежащие ниже главной диагонали равны нулю, то матрица называется верхне-треугольной.

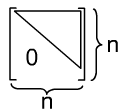
- нижне-треугольная матрица.

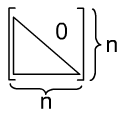
4).

- диагональная матрица.

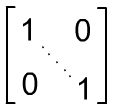
5).

- «единичная» матрица.

Определение 2: Матрицы и одинакового порядка называются равными (запись: = ), если , .

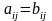Определение 3: Транспонировать матрицу- значит записать строки столбцами с теми же номерами ( столбцы строками с теми же номерами).

Пример: .

Определение 4: Квадратная матрица называется симметричной, если .

Пример: .

Утверждение: , если - симметричная.

Определение 5: Пусть , 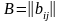, обе матрицы одинакового порядка. Тогда суммой матриц и называется матрица . . .

Определение 6: Пусть и - действительное число. Тогда матрица

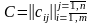
называется произведением матрицы на число , если , { , }

Операции , называются линейными.

Свойства линейных операций над матрицами.

1.

2.

3.

4.

5.

Определение 7: Пусть , . Тогда матрица называется произведением матриц и и обозначается , если { , }.

1. Вообще говоря, .

2.

2. Перестановки, подстановки.

Пусть 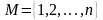- первые натуральных чисел.

Определение 1: Перестановкой - го порядка называется упорядоченная последовательность элементов множества , взятая без пропусков и повторений.

Пример: . Выпишем все возможные перестановки -го порядка:

.

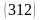
Всего существует возможных перестановок -го порядка.

Замечание: всех возможных перестановок - го порядка.

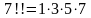
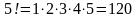
Определение 2: Элементы перестановки образуют инверсию (беспорядок), если , но .

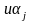Определение 3: Транспозиция элементов и - перемена местами . Все остальные элементы оставляем без изменений.

Определение 4: Обозначим через - общее число инверсий . Если число четное (нечетное), то перестановка называется четной (нечетной).

Утверждение 1. Любая транспозиция меняет четность перестановки.

Доказательство: Пусть меняются местами соседние элементы, тогда справедливость утверждения очевидна. Пусть теперь меняются местами , между которыми элементов:

.

S чисел

Этого можно достичь, меняя местами соседние элементы раз.

Четность перестановки: так как меняем элементы раз, - число нечетное окончательная четность перестановки меняется.

Запишем две перестановки друг под другом, например: и интерпретируем эту запись, как отображение . .

Определение 5: Подстановкой -го порядка называется взаимнооднозначное отображение множества самого в себя по закону, который выражается записью:

. Здесь , … , .

Определение 6: , где - число инверсий в перестановке ,

- число инверсий в перестановке . Если 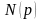- четное число (нечетное), то подстановка называется четной (нечетной).

Очевидно, что одна и та же подстановка -го порядка может быть записана способами (переставляем пары ).

Все записи одной и той же подстановки имеют одинаковую четность.