Нормальная форма и нормализованная форма

Нормальной формой числа с плавающей запятой называется такая форма, в которой мантисса (без учёта знака) находится на полуинтервале [0; 1) ( ). Число с плавающей запятой, находящееся не в нормальной форме, теряет точность по сравнению с нормальной формой.^{[источник не указан 1090 дней]} Такая форма записи имеет недостаток: некоторые числа записываются неоднозначно (например, 0,0001 можно записать в 4 формах — 0,0001·10⁰, 0,001·10⁻¹, 0,01·10⁻², 0,1·10⁻³), поэтому распространена (особенно в информатике) также другая форма записи — нормализованная, в которой мантисса десятичного числа принимает значения от 1 (включительно) до 10 (не включительно), а мантисса двоичного числа принимает значения от 1 (включительно) до 2 (не включительно) ( ). В такой форме любое число (кроме 0) записывается единственным образом. Недостаток заключается в том, что в таком виде невозможно представить 0, поэтому представление чисел в информатике предусматривает специальный признак (бит) для числа 0. Так как старший разряд (целая часть числа) мантиссы двоичного числа (кроме 0) в нормализованном виде равен «1», то при записи мантиссы числа в эвм старший разряд можно не записывать, что и используется в стандарте IEEE 754. В позиционных системах счисления с основанием большим, чем 2 (в троичной, четверичной и др.), этого свойства нет.

5.6 Сложение, вычитание и умножение двоичных чисел

Таблица сложения

+	0	1
0	0	1
1	1	10

Пример сложения «столбиком» (14 + 5 = 19):

		1	↖
+		1	1	1	0
			1	0	1
	1	0	0	1	1

Таблица вычитания

-	0	1
0	0	1
1	1	0

Таблица умножения

×	0	1
0	0	0
1	0	1

7 Если умножение выполняется путем многократных сдвигов и сложений, то деление, будучи операцией обратной умножению,— путем многократных сдвигов и вычитаний.

При представлении чисел с фиксированной запятой деление возможно, если делимое по модулю меньше делителя, в противном случае произойдет переполнение разрядной сетки. Так же, как и при «ручном» делении, разряды частного при делении чисел на машине определяются (начиная со старшего) путем последовательного вычитания делителя из остатка, полученного от предыдущего вычитания. Однако здесь операция вычитания заменяется операцией сложения остатка с отрицательным делителем, представленным в обратном или дополнительном коде. Знак частного определяется сложением по модулю два кодов знаков делимого и делителя.

8. Сложение чисел с плавающей точкой

Так как числа с разными порядками суммировать нельзя, то для сложения двух чисел в нормальной форме представления необходимо выполнить операцию выравнивания порядков.

А = m₁*q^р₁

В = m₂*q^р₂

где m₁, m₂ - мантиссы, р₁ и р₂ - порядки.

Необходимо предварительно привести их к общему порядку, то есть преобразовать одно из слагаемых следующим образом:

Р_общ = max ( p₁*p₂ )

В = (m₂`)*q^р_общ

C = A+B = m*q^p = m₁*q^р_общ+ m₂`*q<sup>р</sup><sub>общ</sub>= (m<sub>1</sub>+(m<sub>2</sub>`))*q^р_общ

Преобразованная мантисса должна быть правильной дробью, поэтому преобразованию всегда подвергается меньшее слагаемое, так как в противном случае может произойти переполнение разрядной сетки мантиссы преобразованного числа.

Пример:

0.4726*10² + 0.9132*10⁰ = 10²(0.4726 + 0.0091) = 0.4817*10² 0.1011₂*2^-1 + 0.1011₂*2¹ = 2¹*(00.0010₂ + 00.1101₂) = 01.0000₂*2¹ = 0.1000₂*2²

Мантисса может переполнить разрядную сетку, при этом использование модифицированных кодов позволяет не только отметить факт переполнения, но и восстановить правильный результат. Это обеспечивается сдвигом мантиссы на одну позицию в сторону младших разрядов и увеличением порядка на 1.

При сложении чисел в нормальной форме можно выделить 4 этапа:

1. Уравниваются порядки слагаемых. Меньший порядок увеличивается до большего, а мантисса преобразуемого числа сдвигается вправо на соответствующее число разрядов. С этой целью производится вычитание порядков чисел. Знак и модуль разности будут определять, соответственно, какое из слагаемых нужно преобразовать и на сколько нужно сдвинуть мантиссу.

2. Производится преобразование мантисс слагаемых в один из модифицированных кодов, дополнительный или обратный, затем производится сложение мантисс по правилу сложения чисел с плавающей точкой.

3. В случае необходимости производится нормализация результатов.

4. Результат переводится в прямой код, ему приписывается общий порядок и округляется.

Умножение чисел

В двоичной системе счисления таблицы умножения описывают функцию коньюкции:

A	B	C
0	0	0
0	1	0
1	0	0
1	1	1

При умножении коньюкция составляет матрицу размером N*N.

Пусть N = 4:

				A	4	3	2	1
				B	4	3	2	1
					14
				24		13
			34		23		12
		44		33		22		11
			43		32		21
				42		31
					41
C	27	26	25	24	23	22	21	20

Разряды сомножителей коньюкции (с 1-го по 4-ый) обозначены двузначными числами, состоящими из номеров разряда сомножителей, а для произведения С указаны веса его разрядов от 2⁰ до 2⁷. Матрица имеет симметричный вид.

Наклонные линии, содержащие коньюкции, являются произведением одного сомножителя на разряд другого. Умножение может выполняться, к примеру, по схеме:

Здесь А и В - множители, N - их разрядность. Начальное значение суммы S устанавливается в блоке 3. В блоке 4 организуется цикл из N итераций (повторений), выполняемых за N тактов . Блок 5 разрешает работу блока 6 лишь при значении В₁= 1 и реализует функцию коньюкторов, умножающих разряды множимого А на первый младший разряд В_i множителя В. Блок 7 сдвигает на 1 позицию вправо числа В и S, при этом место младшего разряда В₁ множителя занимает следующий по старшинству разряд. По окончанию всех итераций блок 8 выводит S - результат умножения.

В данном способе вычисления выполняются начиная с младшего разряда множителя В с изменением взаимного положения чисел S и А путём сдвига суммы S.

Деление чисел

Операция деления выполняется над числами А - делимым и В - делителем. Её результатом является частное С и остаток D.

А = ВС + D,  |D| < В

Операция деления реализуется через многократное вычитание делителя В из делимого А. Это достигается сложением чисел в обратном и дополнительном кодах. Наиболее простой способ деления описывает алгоритм последовательного вычитания:

Если условие А < В не выполняется, то число А умножается на величину В, при этом значение частного увеличивается на 1 и происходит возврат к блоку 4. Если выполняется условие А < В, мы выводим частное С и остаток D.

Описанный алгоритм относится к целочисленному делению и применяется для выполнения операций над числами в естественной форме представления (то есть с фиксированной точкой). Числа с плавающей точкой обрабатываются с использованием точностного деления, которое выполняется над нормализованными мантиссами чисел.

Точностное деление определяет частное с заданным количеством разрядов, а остаток игнорируется. Такое деление характеризуется алгоритмом с восстановлением остатка.

9. Система остаточных классов (СОК) – это непозиционная система счисления, числа в которой представляются остатками от деления на выбранную систему оснований Р1, Р2,...,Рn и являются взаимнопростыми числами. Операции сложения, вычитания и умножения над числами в СОК производятся независимо по каждому основанию без переносов между разрядами (основаниями). Диапазон представимых чисел P=P1ЧP2Ч...ЧPn [4]. Если задан ряд положительных взаимнопростых чисел Р1, Р2,...,Рn, то целое положительное число А, представленное в виде набора наименьших положительных остатков (вычетов) от деления числа А на выбранные основания Р1, Р2,...,Рn, можно записать в виде А=(a1, a2,...,an). Рассмотрим примеры выполнения операций сложения и умножения чисел в СОК. Пусть основаниями системы являются Р1=2, Р2=3, Р3=5, Р4=7. Диапазон представимых чисел в данной системе Р=2Ч3Ч5Ч7=210. Требуется сложить числа А=34 и В=87. По выбранным основаниям числа А и В в СОК будут иметь вид А=(0, 1, 4, 6), В=(1, 0, 2, 3). Сложим числа А и В Легко проверить, что число А+В, представленное по выбранным основаниям как (1, 1, 1, 2), равно 121. Пусть требуется умножить числа А=17 и В=8. А=(1, 2, 2, 3), В=(0, 2, 3, 1). В самом деле, число АхВ, представленное по выбранным основаниям как (0, 1, 1, 3), равно 136. Такие операции, как деление, сравнение и др., требующие информации о величине всего числа, в СОК выполняются по более сложным алгоритмам. И в этом заключается существенный недостаток данной системы счисления, сдерживающий ее широкое применение в качестве компьютерной арифметики. Однако сегодня даже в самых современных компьютерах при работе с большими и супербольшими числами используют СОК, ибо только эта арифметика позволяет получать результаты вычислений в реальном времени. В таких случаях в качестве оснований СОК применяют величины, близкие к 2m (m – двоичная разрядность компьютера), например 2m-1-1, 2m-1, 2m-1+1 и т.д. Компьютер вычисляет результат по одному из модулей за один проход. Другие области применения СОК – помехоустойчивое кодирование, криптография и т.п.

10. Бу́лева фу́нкция (или логи́ческая функция, или функция а́лгебры ло́гики) от n переменных — в дискретной математике — отображение Bⁿ → B, где B = {0,1} — булево множество. Элементы булева множества 1 и 0 обычно интерпретируют как логические значения «истинно» и «ложно», хотя в общем случае они рассматриваются как формальные символы, не несущие определённого смысла. Неотрицательное целое число n называют арностью или местностью функции, в случае n = 0 булева функция превращается в булеву константу. Элементы декартова произведения Bⁿ называют булевыми векторами. Множество всех булевых функций от любого числа переменных часто обозначается P₂, а от n переменных — P₂(n). Булевы функции названы так по фамилии математика Джорджа Буля.

Каждая булева функция арности n полностью определяется заданием своих значений на своей области определения, то есть на всех булевых векторах длины n. Число таких векторов равно 2ⁿ. Поскольку на каждом векторе булева функция может принимать значение либо 0, либо 1, то количество всех n-арных булевых функций равно 2²ⁿ. Поэтому в этом разделе рассматриваются только простейшие и важнейшие булевы функции. То, что каждая булева функция задаётся конечным массивом данных, позволяет представлять их в виде таблицПрактически все булевы функции малых арностей (0, 1, 2 и 3) сложились исторически и имеют конкретные имена. Если значение функции не зависит от одной из переменных (то есть строго говоря для любых двух булевых векторов, отличающихся лишь в значении этой переменной, значение функции на них совпадает), то эта переменная называется фиктивной.

12. Самой первой и наиболее простой, хотя и довольно грубой моделью нейрона является модель "устройства с пороговой логикой" - the Threshold Logic Unit, TLU, более известная по именам американских ученых, разработавших ее в 1943-44 годах. Суть ее состоит в следующем (рис.3).

Рис.3. TLU

Все воздействия и сигналы, передаваемые по сети, кодируются в двоичной форме, по аналогии с цифровыми ЭВМ. Синапсы интерпретируются как модули, выполняющие операцию умножения воздействий на весовые коэффициенты. Эндоплазма нейрона интерпретируется как аддитивный сумматор всех воздействий, помноженных на соответствующие весовые коэффициенты. Полученное результирующее воздействие сравнивается с некоторой пороговой величиной , и в случае ее превышения выдается сигнал, уходящий по (афферентному) аксону ("1"); в противном случае считается, что таковой отсутствует ("0"). Недостатки этой модели:

• Двоичная интерпретация выходного сигнала не учитывает частоты сигналов, которая играет далеко не последнюю роль в реальных нейросистемах;

• В реальных биосистемах практически невозможно встретить скачкообразное изменение величин; кроме того, эта (ступенчатая) модель затрудняет решение множества задач на проектируемых по подобию с живыми нейронами нейроподобных элементах в искусственных нейросетях, реализуемых аппаратно либо эмулируемых программно.

В данном случае работу сети можно описать уравнениями :

• f = 1, если a > ;

• f = 0, если a <= .

Мажорита́рный элеме́нт (мажоритарный клапан, переключатель по большинству, ППБ) — логический элемент из класса пороговых^[1], с чётным или нечётным числом входов и одним выходным сигналом, значение которого совпадает со значением, на большинстве входов.^[2] При чётном числе входов большинством считается n/2+1, соответственно n/2 к большинству не относится^[3]. Таким образом, элемент работает по «принципу большинства»: если на большинстве входов будет сигнал «1», то и на выходе схемы установится сигнал «1»; и наоборот, если на большинстве входов будет сигнал «0», то и на выходе установится «0».^[1]

В бинарных двоичных функциях с унарным выходом, в которых только два входа, мажоритарный клапан «вырождается» в логическую функцию 2И, так как большинством из двух является n/2+1=2/2+1=1+1=1.

Под мажоритарным элементом также понимают устройство, реализующее метод мажоритарного резервирования^[4]. Существующие методы вводят весовые коэффициенты для каждого входного сигнала (пороговые элементы), предысторию и прочие адаптивные алгоритмы.^[4]

Мажоритарные элементы используются в цифровых высоконадёжных системах и устройствах, например, в системах резервирования^[5][4], в помехоустойчивых телекоммуникационных системах^[6][7].

Поскольку нечеткие множества описываются функциями принадлежности, а t-нормы и k-нормы обычными математическими операциями, можно представить нечеткие логические рассуждения в виде нейронной сети. Для этого функции принадлежности надо интерпретировать как функции активации нейронов, передачу сигналов как связи, а логические t-нормы и k-нормы, как специальные виды нейронов, выполняющие математические соответствующие операции. Существует большое разнообразие подобных нейро-нечетких сетей neuro-fuzzy network (англ.) . Например, ANFIS ( Adaptive Neuro fuzzy Inference System) - адаптивная нейро-нечеткая система вывода.^[2] (англ.)

Она может быть описана в универсальной форме аппроксиматоров как

,

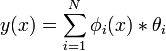кроме того, этой формулой могут быть описаны также некоторые виды нейронных сетей, такие как радиально базисные сети (RBF), многослойные персептроны (MLP), а также вейвлеты и сплайны.

13. Булевы функции одной переменной.

При n = 1 число булевых функций равно 2²¹ = 2² = 4. Определение этих функций содержится в следующей таблице.

Таблица значений булевых функций от одной переменной:

x	0	x̅	x	1
0	0	1	0	1
1	0	0	1	1

Названия булевых функций от одной переменной:

Обозначение	Название
0	тождественный ноль, тождественная ложь, тождественное "НЕТ"
x̅, ¬x, x'	отрицание, логическое "НЕТ", "НЕ", "НИ"
x	тождественная функция, логическое "ДА"
1	тождественная единица, тождественная истина, тождественное "ДА", тавтология

Дизъю́нкция — (лат. disjunctio - разобщение) логическая операция, по своему применению максимально приближённая к союзу «или» в смысле «или то, или это, или оба сразу». Синонимы: логи́ческое «ИЛИ», включа́ющее «ИЛИ», логи́ческое сложе́ние, иногда просто «ИЛИ».

В булевой алгебре дизъюнкция — это функция двух, трёх или более переменных (они же — операнды операции, они же — аргументы функции). Правило: результат равен , если все операнды равны ; во всех остальных случаях результат равен .

Таблица истинности

Конъю́нкция (от лат. conjunctio союз, связь) — логическая операция, по своему применению максимально приближённая к союзу "и". Синонимы: логи́ческое "И", логи́ческое умноже́ние, иногда просто "И".

Конъюнкция может быть бинарной операцией, то есть, иметь два операнда, тернарной операцией, т.е. иметь три операнда или n-арной операцией, т.е. иметь n операндов. Чаще всего встречаются следующие варианты инфиксной записи:

.

В булевой алгебре конъюнкция — это функция двух, трёх или более переменных (они же — операнды операции, они же — аргументы функции). Переменные могут принимать значения из множества . Результат также принадлежит множеству . Вычисление результата производится по простому правилу, либо по таблице истинности. Вместо значений может использоваться любая другая пара подходящих символов, например или или "ложь", "истина". Правило: результат равен , если все операнды равны ; во всех остальных случаях результат равен .

Таблицы истинности: для бинарной конъюнкции

Штрих Ше́ффера — бинарная логическая операция, булева функция над двумя переменными.

Таблица значений

X	Y	X|Y
0	0	1
0	1	1
1	0	1
1	1	0

Как и любую булеву операцию, штрих Шеффера можно выразить через отрицание и дизъюнкцию:

либо через отрицание и конъюнкцию

Импликация (лат. implicatio - связь) — бинарная логическая связка, по своему применению приближенная к союзам «если… то…».

Импликация записывается как посылка следствие; применяются также стрелки другой формы и направленные в другую сторону (остриё всегда указывает на следствие).

Суждение, выражаемое импликацией, выражается также следующими способами:

• Посылка является условием, достаточным для выполнения следствия;

• Следствие является условием, необходимым для истинности посылки.

• В булевой логике импликация — это функция двух переменных (они же — операнды операции, они же — аргументы функции). Переменные могут принимать значения из множества . Результат также принадлежит множеству . Вычисление результата производится по простому правилу, либо по таблице истинности. Вместо значений может использоваться любая другая пара подходящих символов, например или или «ложь», «истина».

Импликация как булева функция ложна лишь тогда, когда посылка истинна, а следствие ложно. Иными словами, импликация  — это сокращённая запись для выражения .

прямая импликация (от a к b) (материальная импликация, материальный кондиционал)

• если , то истинно (1),

обратная импликация (от b к a, )

• если , то истинно (1), обратная импликация — отрицание (негация, инверсия) обнаружения увеличения (перехода от 0 к 1, инкремента).

Стре́лка Пи́рса (символ Лукасевича^{[источник не указан 833 дня]}) — бинарная логическая операция, булева функция над двумя переменными. Введена в рассмотрение Ч. Пирсом (Сh. Peirce).

Стрелка Пирса, обычно обозначаемая ↓, задаётся следующей таблицей истинности:

A	B	A ↓ B
0	0	1
0	1	0
1	0	0
1	1	0

Таким образом, высказывание «A ↓ B» означает «ни A, ни B».

Стрелка Пирса является шефферовой функцией, то есть образует базис для пространства булевых функций от двух переменных. Это означает, что, используя только стрелку Пирса, можно построить все остальные операции, например:

¬x ≡ x↓x

x & y ≡ (x↓x) ↓ (y↓y)

x ∨ y ≡ (x↓y) ↓ (x↓y)

x → y ≡ ((x↓x) ↓ y) ↓ ((x↓x) ↓ y)