Заключение

Подводя итог выше сказанному, нам бы хотелось отметить то, что данная работа, расширила наш кругозор, углубила наши знания в области геометрии, дала дополнительную возможность подготовки к итоговой аттестации.

Задача на вычисление длин, площадей, углов, связанных с плоскими фигурами – довольно сложная задача, часто требующая рассмотрения двух и более случаев, и приводящим к двум разным ответам, в школьном курсе рассматривается очень редко. При решении задач такого рода нужно понять, как выглядит чертеж, для чего необходимо учесть все мыслимые возможности.

Систематическое изучение свойств геометрических фигур способствует формированию пространственных представлений, развитию логического мышления, развитию познавательных интересов, предоставляет возможность подготовиться к сознательному выбору профиля обучения и дальнейшей специализации.

Наша работа может быть эффективно использована на факультативных занятиях в 10 - 11 классах.

Приложение №1

Краткий теоретический курс в таблицах

В основе решения большинства задач лежит умение «решать треугольники», поэтому необходимо вспомним важные соотношения для треугольников. Повторить основные теоритические сведения, основные приемы решения задач можно и с помощью широкого спектра электронных учебных пособий: «Открытая математика 1.0. Планиметрия», «Математика», 5-11кл. Практикум», «Новые возможности для усвоения курса математики! Математика», 5-11кл. Практикум» и т. д.

Можно начертить, проводя соответствующие комментарии, таблицу:

Прямоугольный треугольник	Косоугольный треугольник
1	2
А С В ; - теорема Пифагора; ;	; - теорема косинусов; ; - теорема синусов; ;

Варианты схем:

Равенство углов

Биссектриса угла

В правильных многоугольниках

Перпендикулярные прямые

Углы параллелограммов

Накрест лежащие, соответственные

Вертикальные углы, смежные с равными

Вписанные углы, опирающиеся на одну дугу

Углы при основании равнобедренного треугольника

Равенство отрезков

По определению

Медиана в треугольнике

Середина отрезка

Стороны параллелограммов

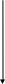
Стороны правильного многоугольника

Теорема Фалеса

Диагонали прямоугольника, квадрата

Боковые стороны равнобедренного треугольника, равнобочной трапеции

Всевозможные формулы нахождения площади треугольника, четырехугольника, правильного шести угольника:

Треугольники	Четырехугольники	Правильные многоугольники
1	2	3
- формула Герона А С В для правильного треугольника	А С a В D - для ромба

Приложение №2

Задача №1

1. Дан треугольник АВС со сторонами АВ=15, АС=9 и ВС=12. На стороне ВС взята точка D, а на отрезке AD – точка О, причем CD=4 и АО=3OD. Окружность с центром О проходит через С. Найдите расстояние от точки С до точки пересечения этой окружности с прямой АВ.

Решение:

Проведем через вершину А прямую, параллельную ВС. Пусть Т – точка ее пересечения с прямой СО, а М – точка пересечения АВ и СТ. треугольник АОТ подобен треугольнику DОС с коэффициентом , поэтому АТ=3CD=12. Значит, треугольник АМТ равен треугольнику ВМС по стороне и двум прилежащим к ней углам. Тогда М- середина стороны АВ. Следовательно, СМ – медиана треугольника АВС.

Через вершину С проведем прямую, параллельную АВ. Пусть Q –точка ее пересечения с прямой АО. Треугольник CDQ подобен треугольнику BDA с коэффициентом , поэтому CQ= . Тогда треугольники АМО и QCO равны по стороне и двум прилежащим к ней углам. Поэтому О – середина СМ.

Пусть N – вторая точка пересечения окружности с прямой АВ. Тогда угол CNM – вписан и опирающийся на диаметр СМ, так что CN AB, то есть CN – высота треугольника ABC. Отсюда CN=

Ответ:7,5 или 7,2

Задача №2

2. Две окружности, касаются прямой в точках А и В, пересекаются в точках С и D, причем АВ=8, CD=15. Найти медиану СЕ треугольника АВС.

Решение:

Пусть F – точка пересечения прямой CD с отрезком АВ. По теореме о касательно и секущей

Значит, АF=FB=4, и F совпадает с Е.

Возможны два случая взаимного расположения точек С,D и Е:

Рис.1

Рис.2

1.ЕС < ED (рис.1).

2.ЕС > ED (рис.2).

Пусть х- длина меньшего из отрезков ЕС и ED, тогда, используя теорему о секущей и касательной, получаем: или .

Значит, . Поэтому СЕ=х=1 или СЕ=х+16

Ответ: 16 или 1.

Задача №3

3. Высота равнобедренного треугольника, опущенная на основание, равна 63, точка касания вписанной окружности с боковой стороной делит эту сторону в отношении 20:9, считая от основания. Найдите радиус окружности, касающейся стороны треугольника и продолжений двух других его сторон.

Решение:

Пусть АD- высота равнобедренного треугольника АВС, опущенная на его основание ВС, О – центр окружности, Р – точка ее касания с боковой стороной АВ. Положим АР=9х, ВР=20х. тогда АВ=АР+ВР=29х, ВD=DP=20x.

По теореме Пифагора , откуда , значит х=3.

Тогда, АР=9Х=27, ВD=20x=60, AB=29x=87.

Обозначим . Из прямоугольного треугольника АВD находим, что

Пусть окружность с центром О1 и радиусом r1 касается продолжений боковых сторон АВ и АС в точках F и G соответственно (рис. 1), а также основания ВС. Тогда – точка касания, поэтому

BF=BD=60, AF=AB+BF=AB+BD=87+60=147.

Следовательно, r1=O1F=

Пусть теперь окружность с центром О2 радиуса r₂ касается боковой стороны АВ, продолжения основания ВС в точке Q и продолжения боковой стороны АС в точке К (рис. 2). Центр окружности, вписанной в угол, лежит на его биссектрисе, поэтому АО2 и АD – биссектрисы смежных углов ВАК и САВ, значит, Тогда ADQO₂ – прямоугольник. Следовательно, r₂=O2Q=ad=63.

Радиус окружности, касающейся боковой стороны АС и продолжений основания ВС и боковой стороны АВ, также равен 63.

Ответ: 63 или 140.

Задача №4

4. Прямая, перпендикулярна гипотенузе прямоугольного треугольника, отсекает от него четырёхугольник, в который можно вписать окружность. Найдите радиус окружности, если отрезок этой прямой, заключенный внутри треугольника, равен40, а отношение катетов треугольника .

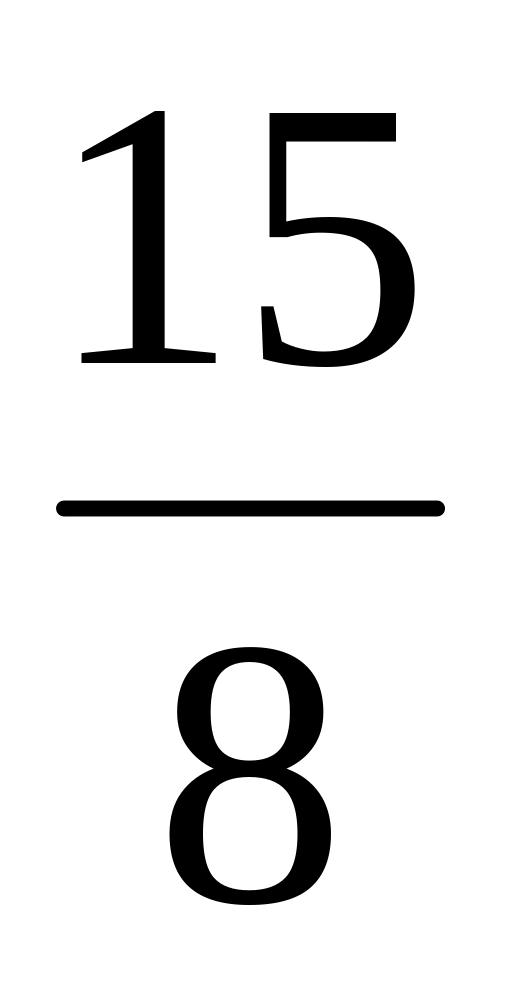Решение:

Обозначим треугольник АВС. Предположим, что отрезок отсекает от треугольника АВС треугольник АNM (рис. 1)

Обозначим точки касания окружности и прямых Р, Q, R, S(рис. 1).

Так как ОQMR и OPCS – квадраты,MQ=PC=r, где r – радикс окружности. Кроме того, NQ=NP. Значит, NM=NC. BN – биссектриса угла АВС. Треугольник NMB и NCB равны по гипотенузе и катету. Пусть СВ=8х, а СА=15х. по теореме Пифагора АВ=17х. тогда АМ=АВ-ВМ=17х-8х=9х. Из подобия треугольников AMN и АСВ получаем: , следовательно, Найдем радиус окружности:

Если отрезок отсекает треугольник BNM (рис. 2), то, рассуждая аналогично, находим, что ВМ=17х-15х=2х. из подобия треугольников АСВ и NMB получаем: , откуда , . Тогда r=3х=32.

Ответ: 25 или 32.

Задача №5

5. Дан ромб АВСD с диагоналями АС=24 и ВD=10. Проведена окружность радиуса с центром в точке пересечения диагоналей ромба. Прямая, проходящая через вершину В, касается этой окружности и пересекает прямую СD в точке М. Найти СМ.

Решение. Пусть точка М лежит между С и D (рис. 1), Р – точка касания прямой ВМ с данной окружностью, О – центр ромба.

По теореме Пифагора

Обозначим Из прямоугольных треугольников ОРВ и СОD находим, что

Применяя теорему синусов к треугольнику ВМD получим, что поэтому

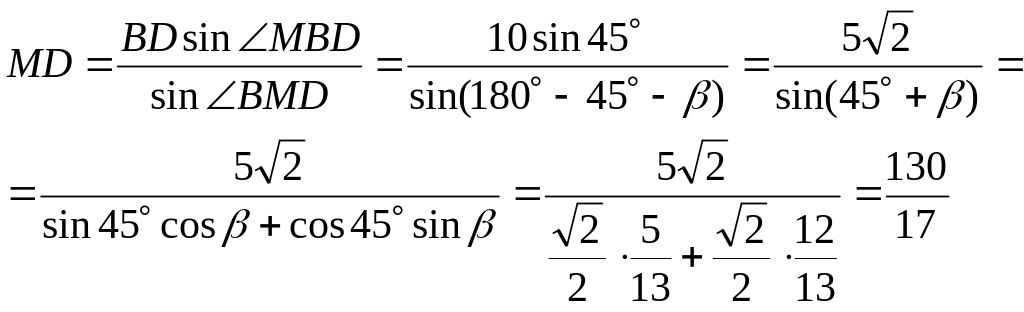
Следовательно, .

Пусть теперь точка М лежит на продолжении стороны CD за точку D (рис. 2) тогда по теореме о внешнем угле треугольника

Далее, рассуждая аналогично, получим, что

Следовательно,

Ответ: .

Приложение №3