Глава 3. Теория автоматов.

ТЕОРИЯ АВТОМАТОВ.

ВВОДНЫЕ ПОЛОЖЕНИЯ.

Теория автоматов – раздел дискретной математики, изучающий математические модели реальных (технических, биологических, экономических) или возможных устройств, перерабатывающих дискретную информацию дискретными временными тактами.

В этой теории достаточно четко выявляются ее направления, обусловленные:

1. выбором изучаемых типов автоматов (конечные, бесконечные, детерминированные, вероятностные, автономные, комбинационные, без выхода)

2. принятым уровнем абстракции (абстрактные и структурные автоматы)

3. спецификой применяемых математических (алгебраическая теория автоматов)

При этом в дискретных моделях рассматриваемых объектов учитывается лишь логика происходящих процессов изменений автомата без учета количественных характеристик.

Центральными проблемами читаемой теории являются проблемы синтаксиса и анализа (т.е. разработка функциональной схемы автомата по заданному его поведению и описание поведения автомата по известной его структуре). С этими проблемами тесно связаны задачи полноты, эквивалентности, минимизации числа состояний автоматов.

Далее автомат, как устройство, предназначенное для выполнения целенаправленных действий без участия человека, рассматривается либо как реализующий ту или иную формальную грамматику (абстрактный автомат), либо как множество элементов и схема их соединения (структурный автомат).

Основные понятия теории автоматов

1. Абстрактный конечный автомат U- модель <A, Q, B, R>, представляющая устройство, которое преобразует информацию по правилам R в виде «черного ящика», имеющего входной А и выходной В алфавиты, а также некоторое множество внутренних состояний Q.

a_i  A_, b_j  B, q_k  Q

Когда на вход подается сигнал a_i, то в зависимости от него и текущего состояния q_k  Q автомат переходит в следующее состояние q_{l } Q и выдает сигнал на выход b_j  B. Это – один такт действия автомата q_k a_i q_l b_j. Затем подается следующий сигнал, наступает следующий такт и т.д. Изменение сигнала на входе меняет состояние автомата и его выходной сигнал означает элементарное преобразование поступающей в виде сигналов информации.

2. Бесконечный автомат – абстрактный автомат, хотя бы одно из определяющих множеств A, B, Q которого бесконечно.

3. Ситохастический (вероятностный) автомат - абстрактный автомат, правила преобразования информации, которого R являются вероятностными.

4. Конечный автомат – дискретный автомат, в котором переход из одного состояния в любое другое может быть совершено за конечное число шагов (таким автоматом, например, является процессор).

5. Структурный автомат - конечный автомат, внутреннее устройство которого известно.

6. Формальная грамматика =<T, H, J, P> - система правил построения P в заданном алфавите TH(T – терминальный алфавит, Н – нетерминальный алфавит, ТН=) конечных знаковых последовательностей, множество которых образует некоторый формальный язык () (JH, Н - аксиома).

7. Формальный язык - язык, построенный по правилам некоторого логического исчисления (иначе – язык, синтаксис которого определен формальной грамматикой ).

8. Слово – цепочка символов в некотором алфавите (принято цепочки в алфавите (TH) обозначать греческими буквами; так, например,  (TH)*).

9. Предложение – слово в терминальном алфавите.

10. Продукция (синтаксическое правило) – способ преобразования цепочки вида  (, ,  (TH)*) в цепочку вида  ((TH)*).

11. Дерево вывода (разбора) – форма наглядного представления вывода предложения в заданной грамматике.

АВТОМАТЫ И ФОРМАЛЬНЫЕ ЯЗЫКИ.

Описание формальных языков (как конечных или бесконечных множеств слов) конечными средствами осуществляют как автоматами, так и формальными грамматиками.

Тип языка () по Хомскому	Тип формальной грамматики Хомского	Автоматная модель языка
0	Произвольная (алгоритмическая) грамматика типа 0 	Машина Тьюринга
1	Грамматика типа 1 (контекстная грамматика, Н.С. грамматика, грамматика непосредственно составляющих) В	Автомат с линейно-ограниченной памятью
2	Грамматика типа 2(контекстно-свободная грамматика, К.С. грамматика, бесконтекстная грамматика) В	Магазинный автомат
3	Грамматика типа 3(автоматная, регулярная, конечная) ВаС, Ва	Конечный автомат

Классы языков по Хомскому являются иерархией, т.е. язык типа 3 является подклассом языка типа 2, т.е. (₃) (₂) (₁)  (₀). Следуя приведенной таблице, можно говорить, что

1. регулярный язык (т.е. язык, порождаемый грамматикой типа 3) распознается конечным автоматом и в этом плане является самым простым в математическом плане

2. бесконтекстный язык (т.е. язык (₂)) распознается магазинным автоматом – бесконечным автоматом, внутренняя структура которого представляет собой стековую память

3. контекстный язык (₁) распознается автоматом с линейно-ограниченной памятью, т.е. автоматом, которому для распознавания последовательности длины nN необходима память объемом не более k*n, где k – число, независящее от входного слова

4. произвольный формальный язык, т.е. (₀), распознается машиной Тьюринга – математического понятия для формального уточнения интуитивного понятия «алгоритм»

Замечание: В синтаксическом правиле В являются контекстами (левый и правый), которые могут быть пустыми цепочками; ВН, а,, ,   (ТН).

ФОРМАЛЬНЫЕ ГРАММАТИКИ.

Формальные грамматики =<T, H, J, P> как процедуры могут быть порождающими и распознающими. Порождающая грамматика по существу является частным случаем формальной системы FS^/=<, D>-<F, D>=<F, S; Ax, P>. В этом случае A=TH, F(TH)^*, JH, P=_i_j_{i, jN}, _i, _j(TH)^*, т.е. правила вывода P позволяют получать слова в терминальном алфавите Т из единственной аксиомы J путем замещения нетерминальных символов цепочек в алфавите (TH).

Распознающая грамматика – алгоритм, распознающий по любой цепочке, является ли оно словом языка  T^*.

Автомат для распознавания и порождения слов можно рассматривать как устройство обработки входных цепочек символов с целью:

1. определения их принадлежности формальному языку ()

2. порождений выходных цепочек символов

Выводом в грамматике  называется последовательность цепочек, в которой каждая из цепочек, кроме первой, получается из предыдущей применением какого-либо правила вывода (последняя цепочка в выводе – предложение, т.е. слово В в алфавите Т).

Пример 1: Т=a, b, c, H=B, C, J=B, P=BaBС, BCc, Cb

Возможным выводом в этой грамматике может быть последовательность слов:

В, аВС, аСсС, аbсС, аbсbТ^*

Эта грамматика порождает язык b, bc, abcb.

Пример 2: множество нечетных чисел в унарном представлении – это множество терминальных слов вида а, ааа, ааааа….., т.е. язык =хТ^*: ха^2n-1, nN. Этот язык порождается автоматной грамматикой ₃=<a, J, J, Ja, JaB, BaJ>.

Пример 3: Язык =хТ^*: х=aⁿbⁿ_nN порождается К.С. грамматикой, т.е. ₂=<a, b, J, J, JaJb, Jab>.

Пример 4: Язык булевых формул с переменными x, y, z порождается К.С. грамматикой ₂=<x, y, z, , , , (,), J, J, J(JJ), J(JJ), JJ, Jx, Jy, JZ>.

ДЕРЕВЬЯ ВЫВОДА ПРЕДЛОЖЕНИЙ.

На практике вывод слов языка () в виде последовательности цепочек часто оказывается громоздким. Кроме того, такой способ не позволяет получить в удобном виде информацию о синтаксических конструкциях. Наилучшим способом компактного представления вывода слов в таком случае является дерево вывода (дерево синтаксического анализа, дерево грамматического разбора). Говорят, что задано стандартное дерево вывода, если правилу r_i: ₁A₂₁₂ (здесь ₁, ₂ – контекст, ₁, ₂ (TH)^*), АН, (TH)^*) поставлено в соответствие элементарное поддерево t(r_i) с вершиной А и кроной ₁_2.

Пример 1: Пусть 1=<a, b, c, A, B, C, D, J, J, JAAB, ABDBB, aBBabB, Aa, Da, BC, Cc>.

Вывод J, AAB, aAB, aDBB, aaBB, aabB, aaaBC, aabc представим деревом:

A

З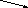десьJ – корень дерева, J A , A a - поддеревья.

B

aabc – крона дерева синтаксического вывода(a, b, b, c – листья дерева ).

Пример 2: Арифметическое выражение a*b+c в К.С. грамматике с продукциями P=JB, JJ+B, BC, BBC, CD, Da, Db, Dc  имеет следующий вывод: J, J+B, B+B, BC+B, CC+B, DC+B, aC+B, ab+B, ab+C, ab+D, ab+c (этот вывод содержит 52 символа). Дерево этого вывода имеет вид:

J

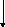
J + B

B C

B * C D

C D c

D b

a

В этом дереве синтаксического вывода 16 вершин, из них 5 помечены терминальными символами (крона а, *, b, +, с), а 11 – нетерминальными (равно числу применения правил в выводе терминальной цепочки a*b+c).

Примечание:

1. Однозначное соответствие между выводом и его синтаксическим деревом не означает однозначность обратного – одному дереву, может соответствовать несколько выводов. Так, в рассмотренном примере арифметическое выражение в грамматике может иметь и другой вывод: J, J+B, B+B, Bc+B, BD+B, Bb+B, Cb+B, Db+B, ab+B, ab+C, ab+D, ab+c, а его дерево тоже самое, что в рассмотренном примере.

К.С. грамматика ₂ может быть нефункциональной, если в ней существует хотя бы одно предложение языка , имеющее более одного дерева синтаксического вывода.