
Задание на ДЗ
.docВычислительная математика
Домашняя работа
I.Элементарная теория погрешностей
-
Выполнить последовательные округления следующих чисел: 2,75464; 3,14159; 0,56453; 4,1945; 0,60653.
-
Округляя следующие числа до трех значащих цифр, определить абсолютную и относительную погрешности полученных приближений: 1,1426; 0,01015; 0,1245; 921,55; 0,002462.
-
Определить абсолютную погрешность следующих приближенных чисел по их относительной погрешности:

 ;
;

 ;
;

 ;
;

 ;
;

 .
. -
Определить количество верных значащих цифр для следующих приближенных чисел:
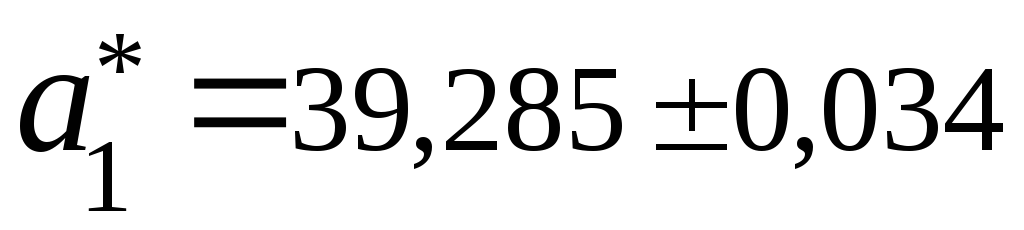 ;
;
 ;
;
 ;
;
 ;
;
 .
. -
По меньшим предельным относительным погрешностям определить, какое из равенств точнее:
 или
или
 ;
;
 или
или
 ;
;
 или
или
 ;
;
 или
или
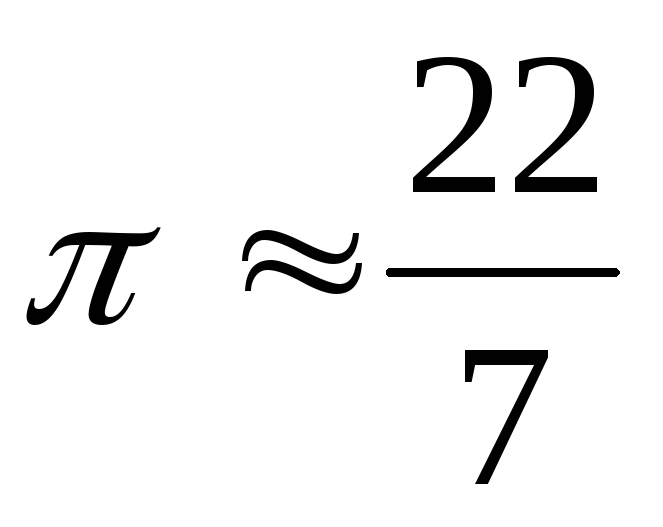 ;
;
 или
или
 .
. -
Округлить сомнительные цифры чисел:
 ;
;
 ;
;
 если
если
 .
. -
Найти предельные абсолютные и относительные погрешности приближенных чисел, заданных только верными цифрами:
 ;
;
 .
. -
Со сколькими верными значащими цифрами надо взять результаты указанных ниже операций, чтобы их предельные относительные погрешности не превышали: 0,1%?
 ;
;
 ;
;
 ;
;
 ;
;
 .
. -
Оценить результаты вычислений выражений, если все операнды заданы со всеми верными цифрами:
 ;
;
 ;
;
 ;
;

-
Пользуясь правилами подсчета цифр, вычислить:
 ;
;

II.Методы решения нелинейных уравнений
-
Отделить корни аналитически и уточнить их до 0,001 методом проб:
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
. -
Отделить корни графически и уточнить их до 0,001 методом хорд:
 ;
;
 ;
;
 ;
;
 ;
;
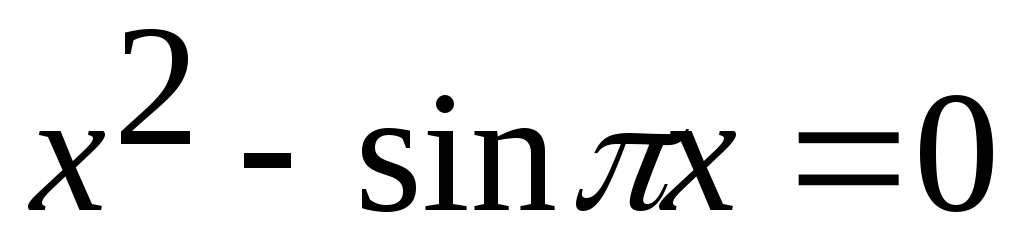 ;
;

-
Методом касательных с точностью до 0,001 найти корни уравнений:
 ;
;
 ;
;
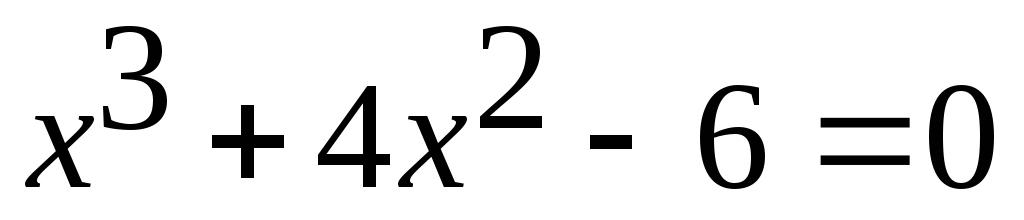 ;
;
 ;
;
 ;
;

-
Комбинированным методом хорд и касательных с точностью до 0,001 найти корни уравнений:
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;

-
Пользуясь методом Штурма, отделить корни уравнений и уточнить их до 0,001 методом итерации:
 ;
;
 ;
;
 ;
;

-
Методом итерации найти корни уравнений с точностью до 0,001:
 ;
;
 ;
;
 ;
;
 ;
;

-
Используя метод Хичкока выделения квадратного множителя, найти с пятью верными цифрами корни уравнений:
 ;
;
 ;
;

III.Методы решения систем линейных уравнений
-
Решить системы уравнений с привлечением формул Крамера:


-
Решить следующие системы по схеме Гаусса:


-
С точностью до 0,001 решить системы по схеме Гаусса:


-
Вычислить определители по схеме Гаусса:


-
Решить следующие системы уравнений с точностью до 0,01 методом последовательных приближений, предварительно определив шагов:


-
Системы линейных уравнений пункта 4 решить методом Зейделя, предварительно определив необходимое число шагов.
IV.Интерполирование и экстраполирование
-
Функцию f (
 ),
), заданную
таблично, определить в точке
заданную
таблично, определить в точке
 =1,5228
с помощью первой интерполяционной
формулы Ньютона.
=1,5228
с помощью первой интерполяционной
формулы Ньютона.
|
|
1,522 |
1,523 |
1,524 |
|
f
( |
20,477 |
20,906 |
21,354 |
-
С помощью второй интерполяционной формулы Ньютона определить значение функции f (
 )
в точке
)
в точке

 =1,5303
если:
=1,5303
если:
|
|
1,529 |
1,530 |
1,531 |
|
f
( |
23,911 |
24,498 |
25,115 |
-

-2
-1
2
3
f (
 )
)-12
-8
3
5
 ),
), заданной
таблично:
заданной
таблично:
-
Построить интерполяционный многочлен Лагранжа для функции
 ,если
узлами интерполяции служат точки
,если
узлами интерполяции служат точки
 ,
, ,
,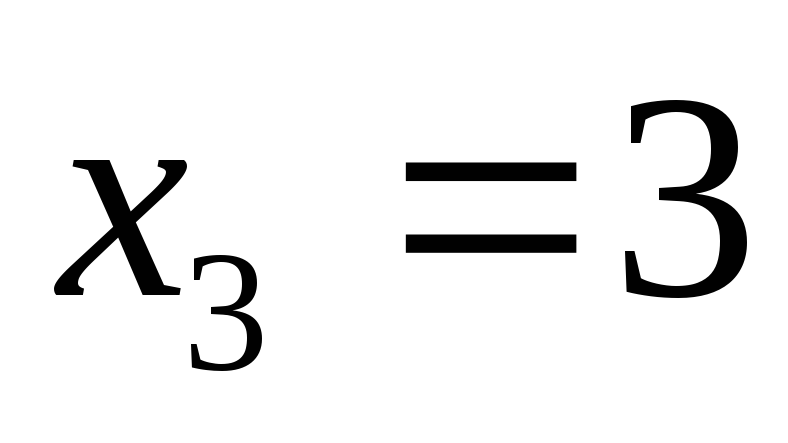 .Оценить
погрешность при
.Оценить
погрешность при
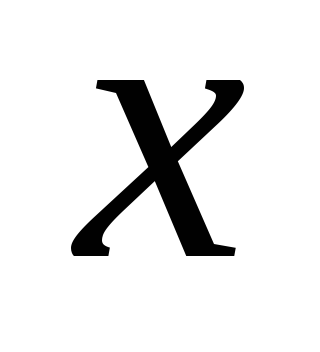 =1,5.
=1,5. -
Для функции f (
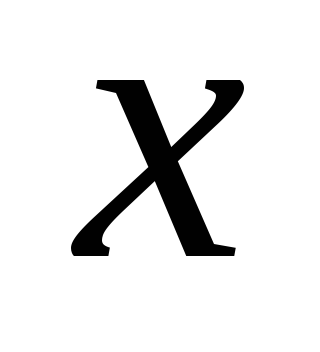 ),
), заданной
таблично составить таблицу конечных
разностей:
заданной
таблично составить таблицу конечных
разностей:

-2
-1
0
1
2
3
f (
 )
)10
5
1
-15
-50
-100
-
Для функции f (
 ),
), заданной
таблично составить таблицу разделенных
разностей:
заданной
таблично составить таблицу разделенных
разностей:

-3
-1
0
2
3
f (
 )
)-15
-7
1
25
47
-
Пользуясь формулой Гаусса, вычислить значение функции f (
 )
в точке
)
в точке
 =1,34627,если:
=1,34627,если:

1,335
1,340
1,345
1,350
1,355
1,360
f (
 )
)4,16206
4,25562
4,35325
4,45522
4,56184
4,67344
-
Для функции f (
 ),
), заданной
таблично определить значение аргумента,
соответствующее значению функции
0,892914.
заданной
таблично определить значение аргумента,
соответствующее значению функции
0,892914.

1,435
1,440
1,445
f (
 )
)0,892687
0,893698
0,894700
-
Методом обратного интерполирования найти с точность до 10-5 корень уравнения
 ,
лежащий в интервале
,
лежащий в интервале
 .
. -
Методом экстраполяции определить значение функции f (
 )
в точке
)
в точке
 =1970,
если известно что:
=1970,
если известно что:

1966
1967
1968
1969
f (
 )
)581
602
625
635
-
Представить аналитически табулированную зависимость:
|
|
1966 |
1968 |
1969 |
|
f
( |
17 |
21 |
23 |
V.Математическая обработка данных
-
Подобрать эмпирическую зависимость в заданном интервале функции и найти параметры методом наименьших квадратов
|
|
1970 |
1971 |
1972 |
1973 |
|
f
( |
623 |
676 |
746 |
829 |
-
Аппроксимировать функцию, заданную таблицей, зависимостью
 и найти параметры методом наименьших
квадратов.
и найти параметры методом наименьших
квадратов.
|
|
1 |
2 |
3 |
4 |
5 |
|
f
( |
2,9 |
8,9 |
19,1 |
33,2 |
50,8 |
-
Представить функцию, заданную таблично, трехпараметрической зависимостью и подобрать коэффициенты методом выбранных точек.
|
|
1950 |
1960 |
1965 |
1970 |
|
f
( |
101 |
106 |
126 |
142 |
