
Некая курсовая по вычислительной математике (Захарова С.С.)
.docxМинистерство образование и науки Российской Федерации
Кафедра Радиоэлектроники
Домашняя работа
по курсу вычислительная математика
по теме
«Решение ОДУ»
Вариант: 30
Выполнил: Носов П.Д.
Проверила: Захарова С. С.
Оценка:
Москва 2009
Задача Коши.
Широкий класс физических задач приводит к ОДУ, разрешенным относительно производной:
|
|
(6.2) |
 - произвольная заданная
функция двух переменных. Должно быть
также задано начальное значение
функции
- произвольная заданная
функция двух переменных. Должно быть
также задано начальное значение
функции
 в точке
в точке
 .
Требуется вычислить неизвестную функцию
.
Требуется вычислить неизвестную функцию
 на отрезке
на отрезке
 .
Такая задача называется задачей Коши.
.
Такая задача называется задачей Коши.
Отметим,
что функция
 должна обязательно присутствовать в
правой части (6.2), вместе с
должна обязательно присутствовать в
правой части (6.2), вместе с
 ,
если же ее там нет, то уравнение решается
путем численного интегрирования функции
,
если же ее там нет, то уравнение решается
путем численного интегрирования функции
 ,
рассмотренного в лекции 4.
,
рассмотренного в лекции 4.
Если
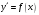 ,
то
,
то
 ,
,
если
же
 ,
то
,
то
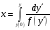 .
.
Решение
задачи Коши - это получение одного
частного решения
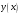 с начальным значением
с начальным значением
 .
Все методы решения этой задачи основаны
на дискретизации и интерполяции, как и
численное дифференцирование, которое
они используют.
.
Все методы решения этой задачи основаны
на дискретизации и интерполяции, как и
численное дифференцирование, которое
они используют.
При
дискретизации на отрезке
 вводится сетка с узлами
вводится сетка с узлами
 ,
,
 .
В простых задачах эта сетка равномерная
и шаг дискретизации равен
.
В простых задачах эта сетка равномерная
и шаг дискретизации равен
 .
При вычислениях выполняется цикл по
шагам, т.е. цикл по
.
При вычислениях выполняется цикл по
шагам, т.е. цикл по
 ,
и на каждом шаге по известному значению
,
и на каждом шаге по известному значению
 вычисляется следующее значение
вычисляется следующее значение
 с применением интерполяции.
с применением интерполяции.
Для
интерполяции функции
 на одном или нескольких шагах используются
полиномы степени
на одном или нескольких шагах используются
полиномы степени
 .
Например,
.
Например,
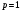 для методов Эйлера (явного и неявного),
для методов Эйлера (явного и неявного),
 для метода Рунге-Кутта четвертого
порядка и метода Адамса,
для метода Рунге-Кутта четвертого
порядка и метода Адамса,
 для модифицированного метода Рунге-Кутта
[K1, Ф, К2]. Степень полинома для интерполяции
называют порядком метода.
для модифицированного метода Рунге-Кутта
[K1, Ф, К2]. Степень полинома для интерполяции
называют порядком метода.
Если при вычислениях на текущем шаге для интерполяции используются только значения функции на одном этом шаге, то методы решения называются одношаговыми, а если для интерполяции используются также значения с предшествующих шагов, то методы называются многошаговыми. Например, метод Адамса является многошаговым, а остальные из перечисленных выше - одношаговыми.
Следует различать порядок метода и порядок ОДУ, т. к. последний равен порядку старшей производной в уравнении. В последующих разделах будут рассматриваться только ОДУ первого порядка, а ОДУ с производными высших порядков см. в лекции 8.
Метод Рунге-Кутта 4-ого порядка.
Этот
одношаговый метод применяется для
решения задачи Коши ( )
и является самым распространенным. В
рассмотренных выше двух методах Эйлера
использовалась линейная интерполяция
)
и является самым распространенным. В
рассмотренных выше двух методах Эйлера
использовалась линейная интерполяция
 на шаге и производная
на шаге и производная
 на каждом шаге вычислялась один раз или
два раза. В методе Рунге-Кутта производные
на шаге вычисляются 4 раза при разных
значениях
на каждом шаге вычислялась один раз или
два раза. В методе Рунге-Кутта производные
на шаге вычисляются 4 раза при разных
значениях
 и
и
 ,
и этот метод эквивалентен выполнению
четырех шагов по методу Эйлера для
получения на текущем шаге искомого
значения
,
и этот метод эквивалентен выполнению
четырех шагов по методу Эйлера для
получения на текущем шаге искомого
значения
 .
.
Введем
обозначение D1
для значений производных, полученных
в левой точке шага (D1)
и в результате выполнения трех
вспомогательных шагов по методу Эйлера
(D2,
D3,
D4),
причем половинные шаги
 дают значения D2
и D3,
а полный шаг
дают значения D2
и D3,
а полный шаг
 - значение D4.
На рис.6.2 даны эти шаги, цифры на прямых
показывают, какому значению - D1,
D2
или D3
- соответствует наклон каждой прямой.
Значения D1,
D2,
D3,
D4
показывают производную в каждой точке
в виде малого отрезка касательной.
- значение D4.
На рис.6.2 даны эти шаги, цифры на прямых
показывают, какому значению - D1,
D2
или D3
- соответствует наклон каждой прямой.
Значения D1,
D2,
D3,
D4
показывают производную в каждой точке
в виде малого отрезка касательной.
|
|
|
Рис.6.2. Вспомогательные шаги в методе Рунге-Кутта. |
Формулы для вычисления значений производных имеют следующий вид:
|
|
(6.8) |
|
|
|
|
|
|
|
|
Полученные
значения
 усредняются с разными весовыми
коэффициентами и основной шаг
усредняются с разными весовыми
коэффициентами и основной шаг
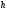 выполняется по (6.3) с полученным средним
значением
выполняется по (6.3) с полученным средним
значением
 :
:
|
|
(6.9) |

Строго
можно показать, что метод Рунге-Кутта
соответствует интерполяции
 полиномом четвертой степени и учитывает
в разложении ряда Тейлора для
полиномом четвертой степени и учитывает
в разложении ряда Тейлора для
 все производные до пятой. Пятая производная
отбрасывается, т.е. абсолютная погрешность
этого метода может быть оценена величиной
все производные до пятой. Пятая производная
отбрасывается, т.е. абсолютная погрешность
этого метода может быть оценена величиной
|
|
(6.10) |
Отметим,
что для метода порядка
 его погрешность на шаге представляется
как
его погрешность на шаге представляется
как
|
|
(6.11) |
т.е.
пропорциональна
 .
Оценку (6.10) следует сравнить с аналогичной
оценкой для метода Эйлера
.
Оценку (6.10) следует сравнить с аналогичной
оценкой для метода Эйлера
|
|
(6.12) |
и из сравнения видим, что метод Рунге-Кутта позволяет использовать существенно более крупные шаги. Это показано на рис.6.3, где пунктирная линия означает точное решение уравнения, полученное, например, с очень мелким шагом или аналитически для специально выбранного уравнения.
|
|
|
Рис
6.3 Интерполяция на шаге для метода
Рунге-Кутта и точное решение уравнения
( |
Метод Эйлера для одного ОДУ первого порядка.
Этот
метод использует линейную интерполяцию
для
 ,
т.е. является методом первого порядка.
Решение (
,
т.е. является методом первого порядка.
Решение ( )
на каждом
)
на каждом
 -ом
шаге вычисляется по формулам:
-ом
шаге вычисляется по формулам:
|
|
(6.3) |
|
|
(6.4) |
где
 - номера шагов,
- номера шагов,
 - величина шага. Для первого шага должны
быть заданы начальные условия, т.е.
значения
- величина шага. Для первого шага должны
быть заданы начальные условия, т.е.
значения
 и
и

Формулу
(6.3) можно рассматривать как начало ряда
Тейлора для функции
 т.к.
т.к.
 по (
по ( ).
Отбрасывание старших производных
означает линейную интерполяцию для
).
Отбрасывание старших производных
означает линейную интерполяцию для
 на шаге.
на шаге.
Эту
же формулу легко получить из ( ).
Значения
).
Значения
 на шаге и
на шаге и
 для наклона касательной показаны на
рис. 6.1. Очевидно, что метод Эйлера
использует на шаге значение
для наклона касательной показаны на
рис. 6.1. Очевидно, что метод Эйлера
использует на шаге значение
 ,
и это значение равно производной в левой
точке шага.
,
и это значение равно производной в левой
точке шага.
|
|
|
Рис.6.1.
Значения
|
Метод
Эйлера является самым простым, но самым
медленным, т.к. линейная интерполяция
на шаге применима обычно лишь для малых
значений
 .
Результат решения - ломаная линия, т.е.
производные
.
Результат решения - ломаная линия, т.е.
производные
 разрывны, но скачки значений
разрывны, но скачки значений
 малы из-за мелких шагов.
малы из-за мелких шагов.
Неявный метод Эйлера.
Рассмотренный
выше метод Эйлера является явным, т.к.
формула (6.3) записана в явном виде и
простой расчет на ЭВМ или калькуляторе
сразу дает значение
 .
Если говорят о методе Эйлера, то всегда
подразумевают явный метод (6.3). Но есть
и неявный метод Эйлера, который существенно
сложнее метода Эйлера. Неявный метод
аналогичен рассмотренному, но на каждом
шаге используется значение
.
Если говорят о методе Эйлера, то всегда
подразумевают явный метод (6.3). Но есть
и неявный метод Эйлера, который существенно
сложнее метода Эйлера. Неявный метод
аналогичен рассмотренному, но на каждом
шаге используется значение
 в правой точке, которое до выполнения
вычислений неизвестно. При этом формула
(6.3) принимает вид
в правой точке, которое до выполнения
вычислений неизвестно. При этом формула
(6.3) принимает вид
|
|
(6.6) |
Здесь
все значения известны, кроме
 .
Так как оно есть и в левой, и в правой
частях (6.6), то для его вычисления нужно
решить нелинейное уравнение вида
.
Так как оно есть и в левой, и в правой
частях (6.6), то для его вычисления нужно
решить нелинейное уравнение вида
|
|
(6.7) |
где
 ,
т.е. неизвестное значение задано неявно.
,
т.е. неизвестное значение задано неявно.
Методы
решения (6.7) были рассмотрены в лекции
5. Следовательно, в неявном методе Эйлера
на каждом шаге нужны итерации для
нахождения корня, что очень сложно.
Поэтому в случае одного уравнения в
форме Коши (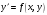 )
неявный метод Эйлера никогда не
применяется, но он широко применяется
в случае систем ОДУ (см. лекцию 8). Отметим,
что при решении ОДУ в общей форме (
)
неявный метод Эйлера никогда не
применяется, но он широко применяется
в случае систем ОДУ (см. лекцию 8). Отметим,
что при решении ОДУ в общей форме ( )
после применения формул численного
дифференцирования на каждом шаге также
получается уравнение (6.7).
)
после применения формул численного
дифференцирования на каждом шаге также
получается уравнение (6.7).
Вывод:
|
Метод |
Шаг |
Погрешность |
Устойчивость |
|
Явный метод Эйлера |
0,001 |
|
|
|
Неявный метод Эйлера |
0,005 |
|
|
|
Метод Рунге-Кутты |
0,05 |
|
|


Явный метод Эйлера
 Неявный
метод Эйлера
Неявный
метод Эйлера
Сравнив
эти методы, мы видим, что наиболее точные
результаты дает метод Рунге-Кутты. При
этом мы используем минимальное количество
шагов. При равных начальных условиях
достоинством метода Рунге-Кутта является
высокая точность, возможность вычислений
с переменным шагом. Метод Эйлера является
самым простым, но самым медленным, т.к.
линейная интерполяция на шаге применима
обычно лишь для малых значений
 .
В неявном методе Эйлера на каждом шаге
нужны итерации для нахождения корня,
что очень сложно. Поэтому в случае одного
уравнения в форме Коши (
.
В неявном методе Эйлера на каждом шаге
нужны итерации для нахождения корня,
что очень сложно. Поэтому в случае одного
уравнения в форме Коши ( )
неявный метод Эйлера никогда не
применяется, но он широко применяется
в случае систем ОДУ.
)
неявный метод Эйлера никогда не
применяется, но он широко применяется
в случае систем ОДУ.

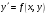 ,
,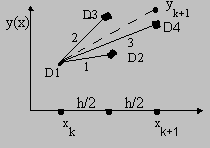
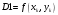



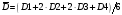

 ,
,

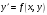 )
)
 ,
,
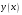 на шагах по методу Эйлера.
на шагах по методу Эйлера.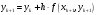
 ,
,




