§ 10. Линейное неоднородное уравнение с постоянными коэффициентами
Рассмотрим линейное неоднородное уравнение
, (1)
где и – заданные постоянные коэффициенты.
Нам
уже известно, что общее решение такого
уравнения складывается из общего решения
,
соответствующего однородного уравнения
(2)
и
какого-нибудь частного решения
уравнения (1), т.е.
. (3)
Как строить общее решение однородного уравнения (2), мы рассмотрим в предыдущем параграфе. Поэтому теперь вопрос об общем решении уравнения (1) сведен лишь к вопросу о построении хотя бы какого-нибудь частного решения уравнения (1). Вообще говоря, можно, например, угадать. Но такой способ определения очень ненадежен. Мы укажем сейчас точные способы, которые всегда приводят к цели.
А. Правая часть уравнения (1) имеет специальный вид
Рассмотрим
функцию:
, (4)
где
– полиномы, а числа m
и n
– вещественные любые.
По
виду этой функции составим «контрольное
число»
.
Пусть
корни характеристического уравнения
будут
и
.
Определим число k следующим образом:
,
если контрольное число не совпадает
ни с одним из корней
;
,
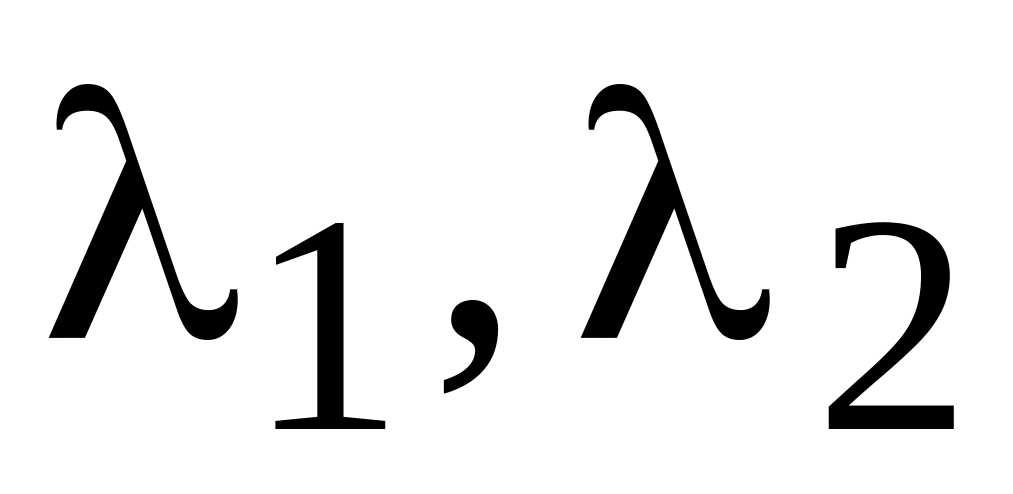если
совпадает с одним из корней
;
,
если
.
Правило. Если правая часть уравнения (1) имеет вид:
(5),
то частное решение следует искать в форме
(6),
где
и
– полиномы степени, равной наивысшей
из степеней полиномов
и
.
Схема нахождения :
зная вид
,
записывают
в форме (3), причем полиномы и
и
записываются с неопределенными
коэффициентами;подставляют в уравнение (1) вместо y, и приравнивают коэффициенты при одинаковых функциях справа и слева. Получают систему уравнений для коэффициентов многочленов
.
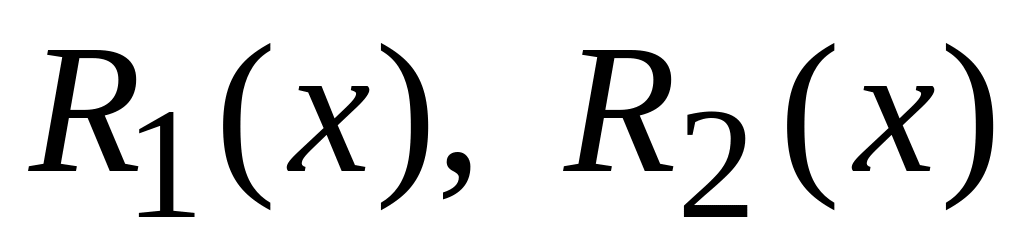Решая эту систему, находят неизвестные
коэффициенты.Найденные коэффициенты подставляют в формулу (3) и находят .
Замечания:
1.
Если функция имеет вид:
или
,
то частное решение
все равно ищется в виде (6) 
.
2.
Если
,
то
.
В этом случае частное решение ищется в
форме:
.
При этом степень
равна степени
и
.
3.
Если
,
то
,
а
имеет вид
.
Пример.
Здесь:
Характеристическое
уравнение
.
Следовательно,
.
Поэтому
следует искать в виде:
Отсюда
Подставляя
в уравнение
и
,
находим:
Отсюда
или
.
Следовательно,
.
В. Метод вариации произвольных постоянных
В пункте А был изложен метод построения для специального вида . Метод вариации произвольных постоянных применим для функции любого вида.
Итак, рассмотрим уравнение (1): , где – любая функция (непрерывная).
Пусть нам известно общее решение однородного уравнения (2)
(7)
где
–
произвольные постоянные, а
и
–
частные решения уравнения (2).
Будем
искать частное решение уравнения (1) в
виде
, (8)
т.е.
в таком же виде, как общее решение (7), но
только вместо произвольных постоянных
подставим пока неизвестные функции.
Найдем их. Поскольку
должно быть решением уравнения (1), то
функции
и
связаны
только одной зависимостью. Для того
чтобы их найти, этого недостаточно.
Поэтому мы вправе наложить на них еще
одно условие по произволу.
Найдем
производную
. 
(9)
Потребуем, чтобы имело бы такой же вид, как если бы и были бы постоянными. Отсюда следует, что должно быть
. (10)
Тогда
. (11)
Найдем
. 
(12)
Подставляя
и
определенные формулами (9), (11) и (12), в
уравнение (1), тогда получим:
или
.
Но и суть решения однородного уравнения (2), поэтому имеем
(13)
Таким
образом,
и
определяются из (10) и (13), т.е. из системы
уравнений
(14)
Эта
неоднородная система линейных
алгебраических уравнений относительно
и
с определителем
.
Это
определитель Вронского, по доказанному
ранее
,
поэтому система (14) имеет единственное
решение. Определение из (14)
и
интегрируя их, найдем
и
,
а затем и
.
Замечание. Если при интегрировании и ввести произвольные постоянные, то сразу получим общий интеграл неоднородного уравнения (1).
Пример.
Соответствующее однородное
Характеристическое
уравнение
.
Общее решение однородного уравнения
Частное
решение заданного уравнения ищем в виде
,
где
и
определяются из системы:
Отсюда
Общее решение будет
или
.