Раздел1_1. Вероятностное пространство. Аксиомы теории вероятности. Классическое определение вероятности.

Пусть Ω - множество всех возможных исходов некоторого испытания (опыта, эксперимента). Каждый элемент ω множества Ω, т.е. ωϵΩ, называют элементарным событием или элементарным исходом, а само множество Ω - пространством элементарных событий. Любое событие А рассматривается как некоторое подмножество множества Ω.

Само множество элементарных событий Ω представляет собой событие, происходящее всегда (при любом элементарном исходе ω), и называется достоверным событием. Т.о., Ω выступает в двух качествах: множества всех элементарных исходов и достоверного события.

Ко всему пространству Ω элементарных событий добавляется еще пустое множество, рассматриваемое как событие и называемое невозможным событием.

Суммой нескольких событий А₁, А₂, …, А_n называется объединение множеств А₁UА₂U…UА_n.

Произведением нескольких событий А₁, А₂, …, А_n называется пересечение множеств А₁∩А₂∩…∩А_n.

Событием Ā, противоположным событию А, называется дополнение множества А до Ω, т.е. Ω\А.

Несколько событий А₁, А₂, …, А_n образуют полную группу (полную систему), если их сумма представляет все пространство элементарных событий, а сами события несовместные, т.е.

Т.о. под операциями над событиями понимаются операции над соответствующими множествами.

Аксиоматическое построение теории вероятностей.

В начале 1930-х гг. академик А.Н. Колмогоров разработал подход, связывающий теорию вероятностей с современной метрической теорией функций и теорией множеств, который в настоящее время является общепринятым.

Аксиомы теории вероятностей

Каждому событию А поставим в соответствие некоторое число, называемое вероятностью события А, т.е. Р(А). Так как любое событие есть множество, то вероятность события есть функция множества.

Вероятность события должна удовлетворять следующим аксиомам:

1. Вероятность любого события неотрицательна: Р(А)≥0.

2. Вероятность достоверного события равна 1: Р(Ω)=1.

3. Вероятность суммы несовместных событий равна сумме вероятностей этих событий, т.е. если 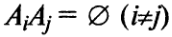, то Р(А₁+А₂+…+А_n) = P(A₁)+P(A₂)+…+P(A_n).

Из аксиом 1, 2, 3 можно вывести основные свойства вероятностей:

1. Р(Ā)=1-Р(А).

2. Р(пустого множества)=0.

3. 0≤Р(А)≤1.

4. Р(А)≤Р(В), если А является подмножеством В.

5. Р(А+В)=Р(А)+Р(В)-Р(АВ).

6. Р(А+В)≤Р(А)+Р(В).

В случае произвольного (не обязательно конечного) пространства элементарных событий Ω аксиому 3 необходимо заменить более сильной, расширенной аксиомой сложения 3’:

Если имеется счетное множество несовместных событий А₁, А₂, …, А_n, …, , то .

Сформулированные аксиомы не определяют условной вероятности одного события относительно другого, которая вводится по определению.

Условная вероятность события В относительно события А есть отношение вероятности произведения событий к вероятности события А, т.е.Р_А(В)=Р(АВ)/Р(А), если Р(А) не равна 0.

Вероятностное пространство определяется тройкой компонент (символов) (Ω, S, P), где Ω - пространство элементарных событий, S – сигма-алгебра событий, P – вероятность.

Компонента S вероятностного пространства – σ-алгебра событий – представляет собой некоторую систему подмножеств пространства элементарных исходов (событий) Ω. Если Ω конечно или счетно, то любое подмножество элементарных исходов является событием, а σ-алгебра есть система всех этих подмножеств. Если же Ω более чем счетно, то оказывается, что не каждое произвольное подмножество Ω может быть названо событием. Причина этого заключается в существовании так называемых неизмеримых подмножеств. Поэтому в таком случае под событием понимается уже не любое подмножество пространства Ω, а только подмножество из выделенного класса S, а σ-алгебра есть система таки подмножеств.

Классическое определение вероятности

Численная мера степени объективной возможности наступления события называется вероятностью события.

Пусть исходы некоторого испытания образуют полную группу событий и равновозможны, т.е. единственно возможны, несовместны и равновозможны. Такие исходы называются элементарными исходами, случаями или шансами.

Случай называется благоприятствующим (благоприятным) событию А, если появление этого случая влечет за собой появление события А.

Согласно классическому определению вероятность события А равна отношению числа случаев, благоприятствующих ему, к общему числу случаев, т.е. Р(А)=m/n, где Р(А) – вероятность события А; m – число случаев, благоприятствующих событию А; n – общее число случаев.

Классическое определение (классическую формулу) вероятности следует рассматривать не как определение, а как метод вычисления вероятностей для испытаний, сводящихся к схеме случаев.

События, вероятности которых очень малы (близки к нулю) или очень велики (близки к единице), называются соответственно практически невозможными или практически достоверными.

Раздел1_2. Случайные величины, функции распределения, их свойства. Абсолютно непрерывные и дискретные распределения. Типовые распределения: биноминальное, пуассоновское, нормальное. Схема Бернулли и полиноминальная схема: основные формулы.

Случайной величиной называют величину, которая в результате испытаний примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены.

Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным.

Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Очевидно, число возможных значений непрерывной случайной величины бесконечно.

Теоретико-множественная трактовка основных понятий теории вероятностей позволяет дать следующее определение случайной величины.

Случайной величиной Х называется функция, заданная на множестве элементарных исходов (или в пространстве элементарных событий). Х = f(ω), где ω – элементарный исход (или элементарное событие, принадлежащее пространству Ω, т.е. ω ϵΩ).

Для дискретной случайной величины множество возможных значений случайной величины, т.е. функции f(ω), конечно или счетно, для непрерывной – бесконечно и несчетно.

Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими вероятностями.

Для дискретной случайной величины закон распределения может быть задан в виде таблицы, аналитически (в виде формулы) и графически.

При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая – их вероятности:

Х х₁ х₂ . . . х_n

p p₁ p₂ . . . p_n

Для любой дискретной случайной величины

Р яд распределения может быть изображен графически, если по оси абсцисс откладывать значения случайной величины, а по оси ординат – соответствующие их вероятности. Соединение полученных точек образует ломаную, называемую многоугольником или полигоном распределения вероятностей.

Функцией распределения случайной величины Х называется функция F(x), выражающая для каждого х вероятность того, что случайная величина Х примет значение, меньшее х. F(x) = P(X<x)

Функцию F(x) иногда называют интегральной функцией распределения или интегральным законом распределения.

Г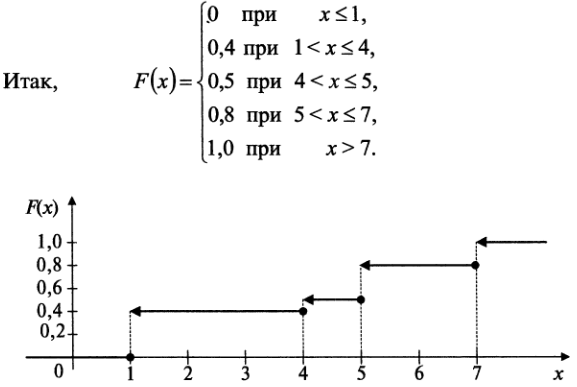 еометрически функция распределения интерпретируется как вероятность того, что случайная точка Х попадет левее заданной точки х.

Функция распределения любой дискретной случайной величины есть разрывная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значениям величины и равны вероятностям этих значений. Сумма всех скачков функции F(x) равна 1.

Свойства функции распределения.

Свойство 1. Значения функции распределения принадлежат отрезку [0;1]: 0≤F(x)≤ 1.

Свойство 2. F(x) – неубывающая функция, т.е. F(x₂)≥F(x₁), если x₂>x₁.

Следствие 1. Вероятность того, что случайная величина примет значение, заключенное в интервале (a, b), равна приращению функции распределения на этом интервале: P(a≤X<b) = F(b) – F(a).

Следствие 2. Вероятность того, что непрерывная случайная величина Х примет одно определенное значение, равна 0.

Свойство 3. Если возможные значения случайной величины принадлежат интервалу (a, b), то: 1) F(x)=0 при x≤a; 2) F(x) = 1 при x≥b.

Следствие. Если возможные значения непрерывной случайной величины расположены на всей оси х, то справедливы следующие предельные соотношения:

Т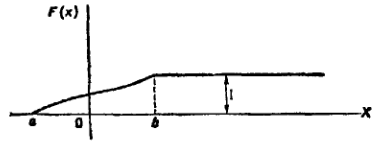 еперь можно дать более точное определение непрерывной случайной величины: случайную величину называют непрерывной, если ее функция распределения есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной.

График функции распределения непрерывной случайной величины, все возможные значения которой заключены в интервале (a, b).

Типовые распределения.

Биномиальный закон распределения.

Пусть производится n независимых испытаний, в каждом из которых событие А может появится либо не появится. Вероятность наступления события во всех испытаниях постоянна и равна p (следовательно, вероятность непоявления q = 1 - p).Рассмотрим в качестве дискретной случайной величины X число появлений события А в этих испытаниях.

Очевидно, событие А в n испытаниях может либо не появится, либо появится 1 раз, либо 2 раза, …, либо n раз.

Дискретная величина Х имеет биномиальный закон распределения с параметрами n и p, если она принимает значения 0,1,2,…,m,…, n с вероятностями

, где 0<p<1, q = 1 – p.

Вероятности P(X=m) находятся по формуле Бернулли.

Т.о. биномиальный закон распределения представляет собой закон распределения числа X=m наступлений события А в n независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью p.

Ряд распределения биномиального закона имеет вид:

Сумма всех вероятностей представляет собой сумму всех членов разложения бинома Ньютона (отсюда и название закона - биномиальный):

Математическое ожидание случайной величины Х, распределенной по биномиальному закону, M(X) = np, а ее дисперсия D(X) = npq.

Пуассоновское распределение.

Поставим задачу найти вероятность того, что при очень большом числе испытаний n, в каждом из которых вероятность p события A очень мала, событие наступит ровно k раз. Сделаем важное допущение: произведение np сохраняет постоянное значение, а именно np=λ. Это означает, что среднее число появлений события в различных сериях испытаний, т.е. при различных значениях n, остается неизменным.

В оспользуемся формулой Бернулли для вычисления интересующей нас вероятности: Так как p=λ/n, то

П риняв во внимание, что n имеет очень большое значение, вместо P_n(k) найдем При этом будет найдено лишь приближенное значение отыскиваемой величины: n хотя и велико, но конечно, а при отыскании предела мы устремим n к бесконечности. Заметим, что поскольку произведение np сохраняет постоянное значение, то при n→∞ вероятность p→0.

Д ля простоты знак приближенного равенства опущен

Ряд распределения Пуассона имеет вид

О пределение закона Пуассона корректно, так как основное свойство ряда распределения выполнено, поскольку сумма ряда (учтено, что в скобках записано разложение в ряд функции е­^х при х = λ).

Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, совпадают и равны параметру λ этого закона, т.е. М(Х)=λ, D(X)=λ.

При p→0, n→∞, np→λ=const закон распределения Пуассона является предельным случаем биномиального закона.

Так как при этом вероятность p события А в каждом испытании мала, то закон распределения Пуассона называют часто законом редких явлений.

Если случайная величина представляет собой сумму двух независимых случайных величин, распределены каждая по закону Пуассона, то она также распределена по закону Пуассона.

Нормальное распределение.

Плотностью распределения вероятностей непрерывной случайной величины Х называют функцию f(x) – первую производную от функции распределения F(x): f(x) = F’(x).

Средним квадратическим отклонением случайной величины Х называют квадратный корень из дисперсии: .

Нормальным называют распределение вероятностей случайной величины, которое описывается плотностью . Вероятностный смысл параметров a и σ таков: a есть математическое ожидание, σ – среднее квалратическое отклонение нормального распределения.

М(Х) = а; D(X) = σ.

Общим называют нормальное распределение с произвольными параметрами a и σ (σ>0).

Нормированным называют нормальное распределение с параметрами a=0 и σ=1.

Функция F(X) общего нормального распределения

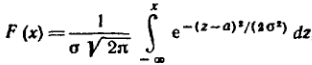
График плотности нормального распределения называют нормальной кривой (кривой Гаусса).

Н ормальная кривая симметрична относительно прямой x=a, имеет максимум в точке x=a, равный и две точки перегиба x=a+σ с ординатой .

Изменение величины параметра a (математического ожидания) не изменяет формы нормальной кривой, а приводит лишь к ее сдвигу вдоль оси Ох: вправо, если а возрастает, и влево, если а убывает.

С возрастанием σ максимальная ордината нормальной кривой убывает, а сама кривая становится более пологой, т.е. сжимает к оси Ох; при убывании σ нормальная кривая становится «островершинной» и растягивается в положительном направлении оси Оу.

Правило трех сигм: если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения.

Центральная предельная теорема (теорема Ляпунова): если случайная величина Х представляет собой сумму очень большого числа взаимно независимых величин, влияние каждой из которых на всю сумму ничтожно мало, то Х имеет распределение, близкое к нормальному.

Схема Бернулли

Теорема. Если вероятность p наступления события А в каждом испытании постоянна, то вероятность P_m,n того, что событие А наступит m раз в n независимых испытаниях, равна , где q=1-p.

Пусть А_i и Ā_i ­– соответственно появление и непоявление события А в i-м испытании (I = 1, 2, …, n), а B_{m ­­­}– событие, состоящее в том, что в n независимых испытания событие а появилось m раз.

Представим событие B_m через элементарные события А_i.

В общем виде B_m = A₁A₂…A_mĀ_m+1…Ā_n + A₁Ā₂A₃…Ā_n-1A_n + … + Ā₁Ā₂…Ā_n-mA_n-m+1…A_n, т.е. каждый вариант появления события В_m (каждый член суммы) состоит из ь появлений события А и n-m непоявлений.

Число всех комбинаций равно числу способов выбора из n испытаний m, в которых событие А произошло, т.е. числу сочетаний С_n^m. Вероятность каждой такой комбинации (каждого варианта появления события B_m) по теории умножения независимых событий равна p^mq^n-m, так как p(A_i)=p, p(Ā_i)=q, I =1, 2, .., n. В связи с тем, что комбинации между собой несовместны, то теореме сложения вероятностей получим .

Число m₀ наступления события А в n независимых испытаниях называется наивероятнейшим, если вероятность осуществления этого события P_m0,n по крайней мере не меньше вероятностей других событий P_m,n при любом m.

np – q ≤ m₀ ≤ np + p.

(Сочетание C_n^m = n!/(m!(n-m)!))

Полиномиальная схема.

В полиномиальной (мультиноминальной) схеме осуществляется переход от последовательности независимых испытаний с двумя исходами (А и Ā) к последовательности независимых испытаний с k исключающими друг друга исходами А₁, А₂, …, А_k. При этом в каждом испытании события А₁, А₂, …, А_k наступают соответственно с вероятностями p₁, p₂, …, p_k. Тогда вероятность P_n (m₁, m₂, …, m_k) того, что в n независимых испытаниях событие А₁ произойдет m₁ раз, А₂ – m₂ раз и т.д., событие A_k – m_k раз (m₁ + m₂ + … + m_k = n) определится по формуле:

В частном случае двух исходов при m₁=m, m₂=n-m, p₁=p, p₂=q, где q=1-p, формула представляет формулу Бернулли.

Раздел4_1. Информация, данные, сигналы. Источники информации и ее носители. Количество информации и энтропия. Формулы Хартли и Шеннона. Характеристики процесса передачи информации. Математические модели каналов связи и их классификация. Помехоустойчивость передачи информации. Пропускная способность каналов связи, характеристики каналов, классификация каналов. Теорема Шеннона для каналов без помех и с ними.

Информация (в теории информации) - совокупность сведений об объектах и явлениях материального мира, рассматриваемых в аспекте их передачи в пространстве и времени.

Данные - это совокупность сведений, которые зафиксированы на каком-либо носителе - бумаге, диске, пленке. Эти сведения должны быть в форме, пригодной для хранения, передачи и обработки. Дальнейшее преобразование данных позволяет получить информацию.

Информация передается в виде сообщений с помощью сигналов.

Сообщение - информация, выраженная в определенной форме и предназначенная для передачи от источника информации к ее получателю с помощью сигналов различной физической природы.

Сигнал - материальный носитель информации, представляющий любой физический процесс, параметры которого адекватно отображают сообщение. По своей физической природе сигналы могут быть электрические, акустические, оптические, электромагнитные и т.д. Изменяющийся во времени физический процесс, отражающий передаваемое сообщение называется сигналом. Сигнал всегда является функцией времени.

В зависимости от того, какие значения могут принимать аргумент (время t) и уровни сигналов их делят на 4 типа:

1. Непрерывный или аналоговый сигналы (случайные сигналы этого типа называются непрерывными случайными процессами).

2. Дискретизированный или дискретно непрерывные сигналы (случайные сигналы этого типа называют процессами с дискретным временем или непрерывными случайными последовательностями). Они определены лишь в отдельные моменты времени и могут принимать любые значения уровня. Временной интервал Dt между соседними отсчетами называется шагом дискретизации. Часто такие сигналы называют дискретными по времени.

3. Дискретные по уровню или квантованные сигналы (случайные сигналы этого типа называют дискретными случайными процессами). Они определены для всех моментов времени и принимают лишь разрешенные значения уровней отделенные друг от друга на величину шага квантования .

4. Дискретные по уровню и по времени сигналы (случайные сигналы этого типа называют дискретными случайными последовательностями). Они определены лишь в отдельные разрешенные моменты времени и могут принимать лишь разрешенные значения уровней.

Источник информации - материальный объект или субъект, способный накапливать, хранить, преобразовывать и выдавать информацию в виде сообщений или сигналов различной физической природы. Выделяют следующие основные источники информации: люди, документы, продукция, средства обработки информации, черновики и отходы производства, материалы и технологическое оборудование.

Носитель информации (информационный носитель) — любой материальный объект или среда, используемый для хранения или передачи информации. Выделяют 4 вида носителей информации: люди, материальные тела (макрочастицы), поля (акустические, магнитные и т. д.), элементарные частицы (микрочастицы).

Количество информации в дискретном сообщении. Энтропия.

Энтропия – это мера хаотичности информации, неопределённость появления какого-либо символа первичного алфавита.

Энтропия – это количество информации, приходящейся на одно элементарное сообщение источника, вырабатывающего статистически независимые сообщения.

Дискретный источник сообщений – это источник сообщений, принимающий случайным образом одно из конечного множества возможных состояний U в каждый момент времени. Совокупность состояний источника называют его алфавитом, а количество состояний N ‑ объемом алфавита.

Мера неопределенности источника с равновероятными состояниями и характеризующего его ансамбля U – это логарифм объема алфавита источника:

(1.1)

Впервые данная мера была предложена Хартли в 1928г. Основание логарифма в формуле не имеет принципиального значения и определяет только масштаб или единицу количества информации.

В общем случае, если вероятности различных состояний источника не одинаковы, степень неопределенности конкретного состояния зависит не только от объема алфавита источника, но и от вероятности этого состояния, тогда

(1.2)

Количество информации в сообщении тем больше, чем оно более неожиданно. Если источник выдает последовательность зависимых между собой элементарных сообщений, то наличие предшествующих сообщений может изменить вероятность последующего, а, значит, и количество информации в нем. Оно должно определяться по условной вероятности выдачи сообщения при известных предшествующих сообщениях ,тогда количество информации будет определятся формулой:

(1.3)

Определения (1.2) и (1.3) количества информации являются случайной величиной, поскольку сами сообщения являются случайными.

(1.4 а) – формула Шеннона.

В тоже время энтропия по Шеннону это среднее количество информации содержащееся в одном из не равновероятных состояний. Она позволяет учесть статистические свойства источника информации.

Формула Хартли – частный случай формулы Шеннона для равновероятных альтернативных событий. Подставив в формулу (1.4 a) вместо , которое в равновероятном случае не зависит от i, значение , получим:

(1.4 b) – формула Хартли.

Из (1.4 b) следует, что чем больше количество альтернатив N, тем больше неопределенность H. Эти величины связаны в формуле (1.4 b) не линейно, а через двоичный логарифм. Логарифмирование по основанию 2 и приводит количество вариантов к единицам измерения информации – битам. Энтропия будет являться целым числом лишь в том случае, если N является степенью числа 2.

Свойства энтропии:

1. Энтропия любого дискретного ансамбля не отрицательна (1.5).

2. Пусть N - объем алфавита дискретного источника, тогда 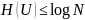(1.6). Равенство имеет место, когда все сообщения источника равновероятные.

3. Энтропия объединения нескольких независимых статистических источников сообщений равна сумме энтропии исходных источников ‑ свойство аддитивности энтропии.

Характеристики процессов передачи информации

В процессе передачи информации участвуют следующие компоненты: источник, приемник и носитель информации, а также среда передачи.

Обычно источники передают сообщения, с некоторой скоростью, затрачивая в среднем время Т на передачу одного сообщения.

Производительность. источника  назовем суммарную энтропию сообщений переданных за единицу времени

 (1.7)

Производительность измеряется в битах на секунду. Если сообщение может быть представлено в виде последовательности элементарных дискретных сообщений   источника с энтропией  следующих со скоростью  элементов в секунду, то

  (1.8)

Аналогичным образом, т.е. разделив в формулах количество информации на Т и

обозначая   получим соответственные равенства для условных энтропии и количества информации, рассчитанных на одно сообщение a в единицу времени.

Величина  называется скоростью передачи информации от U к Z или наоборот. Если, например U ансамбль сигналов на входе дискретного канала, а Z ансамбль сигналов на его выходе то скорость передачи информации по каналу

(1.9).

Здесь H'(U) производительность источника передаваемого сигнала U, а   "производительность" канала, т.е. полная собственная информация в принятом сигнале за единицу времени. Величина  представляет собой потерю информации или ненадежность канала в единицу времени, а  скорость создания ложной, посторонней информации в канале не имеющей отношение к U и обусловленная присутствующими в канале помехами.

Математические модели каналов связи и их классификация

Канал - это комплекс технических средств, обеспечивающий передачу сигналов от передатчика к приемнику. В состав канала входит каналообразующая аппаратура, осуществляющая сопряжение выходного и входного сигналов соответственно передатчика и приемника с линией связи, и самой линии связи. Основное назначение канала связи – это перенос сигнала во времени и в пространстве.

Линией связи называется среда, используемая для передачи сигнала от передатчика к приемнику. Это может быть, например: пара поводов, коаксиальный кабель, область распространения радиоволн, световод и т.д.

В общем случае в процессе передачи в канале сигнал искажается шумом.

Простейшая модель канала связи - дискретная модель канала без памяти. Он определяется следующим образом:

• На входе алфавит –

• На выходе алфавит –

Каждая буква выходной последовательности зависит только от буквы, стоящей на соответствующей позиции во входной последовательности и определяется условной вероятностью

Пример: двоичный симметричный канал.

Важная задача при конструировании канала передачи – анализ искажения. Искажения характеризуются амплитудными и фазовыми характеристиками канала. Для анализа этого надо иметь математическое описание канала.

Анализ канала связи – это анализ искажения сигналов в совокупности с анализом влияния помех.

Помехоустойчивость процесса передачи информации – это способность составных частей системы передачи информации выполнять свои функции надлежащим образом при наличии помех.

Помехоустойчивость оценивается интенсивностью помех, при которых нарушение функций отдельных устройств или всей системы в целом ещё не превышает допустимых пределов. Чем сильнее помеха, при которой система остаётся работоспособной, тем выше её помехоустойчивость.

Пропускная способность каналов связи.

В общем случае, если имеется N элементарных импульсов с вероятностями их появления в сообщении , то можно найти среднюю информацию, связанную с передачей одного импульса 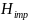– это то количество информации, которое в среднем проходит по данному каналу связи за время . Отношение и , очевидно, будет отражать среднее количество информации, передаваемое по каналу за единицу времени – эта величина является характеристикой канала связи и называется пропускной способностью канала – C :

(1.16)

Если выражено в битах, а – в секундах, то единицей измерения C будут бит/с.

Пропускная способность и помехоустойчивость являются основными характеристиками каналов связи.

Каналы классифицируются:

1. По дипапзону частот: (Километровые (ДВ), Гектометровые (СВ), Декаметровые (КВ), Метровые (МВ), Дециметровые (ДМВ), Сантиметровые (СМВ), Миллиметровые (ММВ), Децимилимитровые (ДММВ));

2. По направленности  линий связи: направленные (с использованием различных проводников: коаксиальные, витые пары на основе медных проводников, волоконнооптические); ненаправленные(радиолинии): прямой видимости; тропосферные; ионосферные; космические; радиорелейные (ретрансляция на дециметровых и более коротких радиоволнах).

3. По виду передаваемых сообщений: телеграфные; телефонные; передачи данных; факсимильные.

4. По виду сигналов: аналоговые; цифровые; импульсные.

5. По виду модуляции (манипуляции): В аналоговых системах связи: с амплитудной модуляцией; с однополосной модуляцией; с частотной модуляцией; В цифровых системах связи: с амплитудной манипуляцией; с частотной манипуляцией; с фазовой манипуляцией; с относительной фазовой манипуляцией; с тональной манипуляцией (единичные элементы манипулируют поднесущим колебанием (тоном), после чего осуществляется манипуляция на более высокой частоте).

6. По значению базы радиосигнала: широкополосные (B>> 1); узкополосные  (B»1).

7. По количеству одновременно передаваемых сообщений: одноканальные; многоканальные (частотное, временное, кодовое разделение каналов);

8. По направлению обмена сообщений: односторонние; двусторонние.

9. По порядку обмена сообщения: симплексная связь, дуплексная связь, полудуплексная связь.

10. По способам защиты передаваемой информации: открытая связь; закрытая связь (засекреченная).

11. По степени автоматизации обмена информацией: неавтоматизированные - управление радиостанцией и обмен сообщениями выполняется оператором; автоматизированные - вручную осуществляется только ввод информации; автоматические - процесс обмена сообщениями выполняется между автоматическим устройством и ЭВМ без участия оператора.

Теорема Шеннона для канала без помех (первая теорема Шеннона)

Для дискретного канала без помех формулировка теоремы Шеннона сводится к следующему.

Если поток информации, вырабатываемый источником, достаточно близок к пропускной способности канала, то всегда можно найти такой способ кодирования, который обеспечит передачу всех сообщений, вырабатываемых источником, причем, скорость передачи информации будет весьма близка к пропускной способности канала.

Это утверждение имеет следующую форму математической записи:

где   - скорость передачи информации; С – пропускная способность канала; σ - сколь угодно (бесконечно) малая величина.

Теорема Шеннона для канала с помехами (вторая теорема Шеннона)

Вторая теорема Шеннона гласит, что при наличии помех в канале всегда можно найти такую систему кодирования, при которой сообщения будут переданы с заданной достоверностью. Для дискретного канала с помехами теорема утверждает, что, если скорость создания сообщений меньше или равна пропускной способности канала, то существует код, обеспечивающий передачу со сколь угодно малой частотой ошибок.

Доказательство теоремы основывается на следующих рассуждениях. Первона­чально последовательность Х={х_i} кодируется символами из В так, что достигает­ся максимальная пропускная способность (канал не имеет помех). Затем в последо­вательность из В длины n вводится r символов и по каналу передается новая после­довательность из n + r символов. Это позволяет определять на приемной стороне канала, какому подмножеству принадлежит искаженная помехами принятая последовательность длины n + r, и тем самым восстановить исходную последовательность длины n.

Раздел5_2. Доктрина информационной безопасности РФ. Основные направления реализации информационной безопасности РФ. Модели систем обеспечения информационной безопасности. Основные этапы разработки систем обеспечения информационной безопасности.

Доктрина ИБ РФ утверждена приказом Президентом РФ № 1895 от 9 сентября 2000 г. и представляет собой совокупность официальных взглядов на цели, задачи, принципы и основные направления обеспечения ИБ РФ.

Доктрина служит основой для:

- формирования государственной политики в области обеспечения ИБ РФ;

- подготовки предложений по совершенствованию правового, методического, научно - технического и организационного обеспечения ИБ РФ;

- разработки целевых программ обеспечения ИБ РФ.

Под ИБ РФ понимается состояние защищенности ее национальных интересов в информационной сфере, определяющихся совокупностью сбалансированных интересов личности, общества и государства.

Общие методы обеспечения ИБ РФ разделяются на правовые, организационно - технические и экономические.

ИБ РФ является одной из составляющих национальной безопасности РФ и оказывает влияние на защищенность национальных интересов РФ в различных сферах жизнедеятельности общества и государства.

В сфере экономики основными мерами по обеспечению ИБ РФ являются:

- организация и осуществление государственного контроля за созданием, развитием и защитой систем и средств сбора, обработки, хранения и передачи статистической, финансовой, биржевой, налоговой, таможенной информации; разработка и внедрение в эти системы национальных сертифицированных средств ЗИ

- коренная перестройка системы государственной статистической отчетности в целях обеспечения достоверности, полноты и защищенности информации;

- разработка и внедрение национальных защищенных систем электронных платежей на базе интеллектуальных карт, систем электронных денег и электронной торговли, стандартизация этих систем;

- совершенствование нормативной правовой базы, регулирующей информационные отношения в сфере экономики;

- совершенствование методов отбора и подготовки персонала для работы в системах сбора, обработки, хранения и передачи экономической информации.

В сфере внутренней политики:

- создание системы противодействия монополизации отечественными и зарубежными структурами составляющих информационной инфраструктуры;

- активизация контрпропагандистской деятельности, направленной на предотвращение негативных последствий распространения дезинформации о внутренней политике России.

В сфере внешней политики:

- разработка основных направлений государственной политики в области совершенствования информационного обеспечения внешнеполитического курса РФ;

- разработка и реализация комплекса мер по усилению ИБ информационной инфраструктуры федеральных органов исполнительной власти, реализующих внешнюю политику РФ, российских представительств и организаций за рубежом, представительств РФ при международных организациях;

- создание российским представительствам и организациям за рубежом условий для работы по нейтрализации распространяемой там дезинформации о внешней политике РФ;

- совершенствование информационного обеспечения работы по противодействию нарушениям прав и свобод российских граждан и юридических лиц за рубежом;

- совершенствование информационного обеспечения субъектов РФ по вопросам внешнеполитической деятельности, которые входят в их компетенцию.

В области науки и техники.

Реальный путь противодействия угрозам ИБ РФ в области науки и техники - это совершенствование законодательства РФ, регулирующего отношения в данной области, и механизмов его реализации. В этих целях государство должно способствовать созданию системы оценки возможного ущерба от реализации угроз наиболее важным объектам обеспечения ИБ РФ в области науки и техники.

В сфере духовной жизни:

- развитие в России основ гражданского общества;

- создание социально - экономических условий для осуществления творческой деятельности и функционирования учреждений культуры;

- выработка цивилизованных форм и способов общественного контроля за формированием в обществе духовных ценностей, отвечающих национальным интересам страны, воспитанием патриотизма и гражданской ответственности за ее судьбу;

- совершенствование законодательства РФ, регулирующего отношения в области конституционных ограничений прав и свобод человека и гражданина;

- государственная поддержка мероприятий по сохранению и возрождению культурного наследия народов и народностей РФ;

- разработка действенных организационно - правовых механизмов доступа СМИ и граждан к открытой информации о деятельности федеральных органов государственной власти и общественных объединений, обеспечение достоверности сведений о социально значимых событиях общественной жизни, распространяемых через СМИ;

- введение запрета на использование эфирного времени в электронных СМИ для проката программ, пропагандирующих насилие и жестокость, антиобщественное поведение;

- противодействие негативному влиянию иностранных религиозных организаций и миссионеров.

В общегосударственных информационных и телекоммуникационных системах.

Основными организационно - техническими мероприятиями по ЗИ в общегосударственных информационных и телекоммуникационных системах являются:

- лицензирование деятельности организаций в области ЗИ;

- аттестация объектов информатизации по выполнению требований обеспечения ЗИ при проведении работ, связанных с использованием сведений, составляющих государственную тайну;

- сертификация средств ЗИ и контроля эффективности их использования, а также защищенности информации от утечки по техническим каналам систем и средств информатизации и связи;

- введение территориальных, частотных, энергетических, пространственных и временных ограничений в режимах использования ТС, подлежащих защите;

- создание и применение информационных и автоматизированных систем управления в защищенном исполнении.

В сфере обороны главными специфическими направлениями совершенствования системы обеспечения ИБ РФ являются:

- систематическое выявление угроз и их источников, структуризация целей обеспечения ИБ в сфере обороны;

- проведение сертификации общего и специального ПО, пакетов прикладных программ и средств ЗИ в существующих и создаваемых АС управления военного назначения и системах связи;

- постоянное совершенствование средств ЗИ от НСД, развитие защищенных систем связи и управления войсками и оружием, повышение надежности специального ПО;

- совершенствование структуры функциональных органов системы обеспечения ИБ в сфере обороны и координация их взаимодействия;

- совершенствование приемов и способов стратегической и оперативной маскировки, разведки и радиоэлектронной борьбы, методов и средств активного противодействия информационно - пропагандистским и психологическим операциям вероятного противника;

- подготовка специалистов в области ИБ в сфере обороны.

В правоохранительной и судебной сферах:

- создание защищенной многоуровневой системы интегрированных банков данных оперативно - разыскного, справочного, криминалистического и статистического характера на базе специализированных информационно - телекоммуникационных систем;

- повышение уровня профессиональной и специальной подготовки пользователей информационных систем.

В условиях чрезвычайных ситуаций. К специфическим для данных условий направлениям обеспечения ИБ относятся:

- разработка эффективной системы мониторинга объектов повышенной опасности, нарушение функционирования которых может привести к возникновению ЧС, и прогнозирования ЧС;

- совершенствование системы информирования населения об угрозах возникновения ЧС, об условиях их возникновения и развития;

- прогнозирование поведения населения под воздействием ложной или недостоверной информации о возможных ЧС и выработка мер по оказанию помощи большим массам людей в условиях этих ситуаций;

- разработка специальных мер по защите ИС, обеспечивающих управление экологически опасными и экономически важными производствами.

Система обеспечения ИБ РФ предназначена для реализации государственной политики в данной сфере. Основными элементами организационной основы системы обеспечения ИБ РФ являются: Президент РФ, Совет Федерации Федерального Собрания РФ, Государственная Дума Федерального Собрания РФ, Правительство РФ, Совет Безопасности РФ, федеральные органы исполнительной власти, межведомственные и государственные комиссии, создаваемые Президентом РФ и Правительством РФ, органы исполнительной власти субъектов РФ, органы местного самоуправления, органы судебной власти, общественные объединения, граждане, принимающие в соответствии с законодательством РФ участие в решении задач обеспечения ИБ РФ.

Модели систем обеспечения ИБ

Модель – способ существования знаний, система – средства достижения цели. При разработке моделей систем ИБ используются различные классы моделей:

1)Модель «чёрного ящика»

Система представляется как некоторая изолированная часть.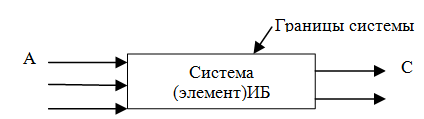

Дополнительные воздействия изменяют лишь некоторые параметры результатов воздействия (С).

Модель чёрного ящика не даёт представления о структуре системы. В ряде случаев такая система является единственно возможной для моделирования какой-либо системы. Она характеризуется недостатком информации или недостаточным уровнем наших знаний. Эта модель разрабатывается на начальных этапах создания системы.

2)Модель состава системы

Она предназначена для того, чтобы определить примерную структуру системы. Модель является иерархической. Уровень иерархии определяется целями, которые были поставлены при разработке системы.

Модель состава системы требует больших объёмов информации о ТС различного назначения (ср-ва пожарн.сигн., ср-ва связи и т.д). Эта задача оказывается сложнее в случае, когда осуществляется доработка в имеющемся помещении, занятых определенными службами.

Эта модель позволяет установить часть причинно-следственных связей, она может быть разработана в виде списковой структуры с обозначением подчиненности структурных элементов.

3 )Модель отношений

Она устанавливает возможные физические связи между структурными элементами, разрабатывается в виде бинарной матрицы, по осям которой указаны структурные элементы, а на поле матрицы обозначаются виды бинарных связей.

Модель отношений позволяет систематически, без пропусков проанализировать связи между всеми элементами.

4)Модель «структурная схема системы»

На структурной схеме отражается состав системы и ее внутренние связи. Наряду с термином "связь" нередко употребляют термин "отношение". Наглядным способом описания структурной модели системы являются графы. На рисунке в виде ориентированного графа приведена структурная модель компьютера.

С трелки обозначают информационные связи между элементами системы. Направление стрелок указывает на направление передачи информации.

Основные этапы разработки систем обеспечения ИБ:

1.Анализ состава и содержания конфиденциальной информации;

2.Анализ ценности информации. Определение ущерба от потерь;

3.Анализ внешней среды. Определение потенциального противника;

4.Анализ уязвимости информации;

5.Анализ действующей системы защиты информации;

6.Замысел создания системы ИБ или модернизация существующей;

7.Оценка возможных затрат на разработку системы ИБ или модернизацию существующей;

8.Принятие решения;

9.Разработка проекта системы ИБ или модернизации существующей;

10.Разаработка плана внедрения системы ИБ. Реализация плана внедрения;

11.Утверждение состава лиц, ответственных за ЗИ и их обучение;

12.Опытная эксплуатация системы ИБ;

13.Сдача в эксплуатацию системы ИБ и управление её функционированием.