Тема 5.

ОСНОВНЫЕ ГАЗОДИНАМИЧЕСКИЕ УРАВНЕНИЯ ДЛЯ ТУРБОМАШИН

Основными уравнениями газодинамики, используемыми при расчете турбомашин, являются: уравнение неразрывности, уравнение движения, уравнение сохранения энергии, уравнение момента количества движения. Эти уравнения выводятся применительно к элементарной струйке газа, размеры поперечного сечения которой малы, что позволяет считать постоянными в любом сечении скорости и параметры состояния газа. Затем эти уравнения распространяются на весь поток газа в проточной части турбомашины путем введения в расчет средних значений скоростей и параметров состояния газа.

1. Уравнение неразрывности

В дифференциальной форме в общем виде

Для установившегося движения

На основе формулы Остроградского-Гауса выводится уравнение неразрывности (расхода) в интегральном виде

,

т.е. для установившегося одномерного потока газа массовый расход через любое сечение канала остается постоянным.

При =const (для жидкости) получаем ,

Если уравнение для массового расхода прологарифмировать, а затем продифференцировать, то получим уравнение неразрывности в дифференциальном виде

или

2. Уравнение движения сплошной среды

Это уравнение является выражением второго закона механики Ньютона применительно к жидкой сплошной среде. Оно связывает скорость, плотность и давление с координатами и временем и записывается в разных формах: в форме Эйлера, в форме Новье-Стокса, в форме Громеко-Лэмба, в форме Рейнольдса. Например уравнение Эйлера в векторной форме имеет вид

,

где - вектор ускорения массовых сил.

2.1. Неподвижный канал

Из уравнения движения в форме Эйлера можно получить уравнение Бернулли для идеальной жидкости, движущейся в неподвижном канале

, Дж/кг, (1)

т.е. полная удельная энергия потока жидкости остается постоянной для любого сечения неподвижного канала.

Если каждый член уравнения (1) разделить на g, то получим уравнение Бернулли в единицах столба жидкости, м.

, м, при =const получаем ,

Если каждый член уравнения (1) умножить на , то получим уравнение Бернулли в единицах давления, Па.

, Па.

При движении газов в элементах проточной части динамических машин энергией положения обычно пренебрегают, потому что она намного меньше кинетической энергии и потенциальной энергии давления. Тогда уравнение (1) записывается в виде

, Дж/кг, (1)

Для изоэнтропного процесса можно получить

Тогда

, или .

2.2 Вращающийся канал.

Из треугольников скоростей

В турбине или компрессоре газ перемещается по вращающимся межлопаточным каналам. Это значит, что движение газа в этом случае можно разложить на относительное, переносное и абсолютное. Для рассмотрения относительного движения вводится система координат, связанная с рабочим колесом. В газодинамической теории идеальных лопаточных машин относительное движение считается установившимся, вихревым, а абсолютное движение - неустановившимся, безвихревым (потенциальным).

Из уравнения движения в форме Эйлера можно вывести также уравнение Бернулли для относительного движения без учета трения; для любого сечения межлопаточного канала удельная энергия канала остается постоянной

,

(2)

где W – относительная скорость движения частицы рабочего тела;

U=r – переносная скорость (окружная скорость точки колеса, с которой в данный момент совпадает частица рабочего тела).

При =const

,

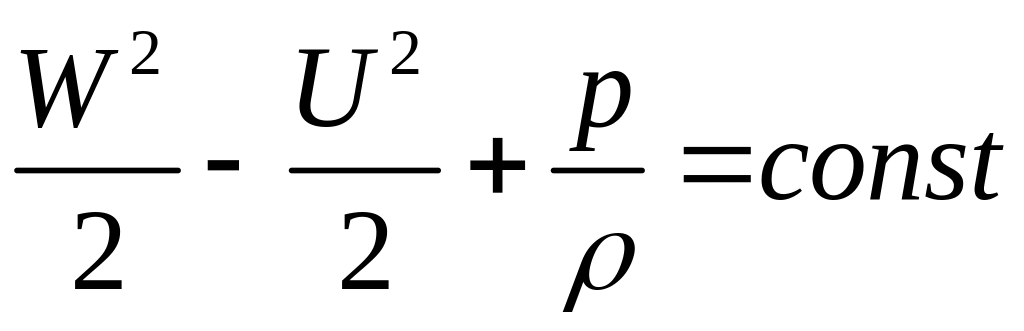Для изоэнтропного процесса: ;

,

или

.

Изменение энергии в относительном движении в пределах межлопаточного канала РК будет равно нулю

,

Тогда изменение удельной потенциальной энергии давления

Из уравнения видно, что увеличение давления газа в пределах межлопаточного канала рабочего колеса происходит за счет увеличения окружной скорости и уменьшения относительной скорости.

Для абсолютного движения газа в пределах межлопаточного канала рабочего колеса в любом сечении канала полная удельная энергия будет равна

С учетом (2) получаем

Тогда изменение полной удельной энергии газа в пределах межлопаточного канала рабочего колеса равно

.

Эта энергия в виде работы отдается от газа внешним телам (например, лопаткам рабочего колеса в турбине) или подводится к газу, движущемуся в межлопаточных каналах рабочего колеса извне (например, со стороны лопаток в компрессоре).