Вопрос 1.

1-й закон термодинамики для закрытой термодинамической системы. Энтальпия

Пусть некоторому рабочему телу (термодинамической системе) объемом V и массой М, имеющему температуру Т и давление р, сообщили извне некоторое количество теплоты dQ. В результате этого тело нагреется на температуру dT и увеличится в объеме на dV. Из-за повышения температуры тела увеличится кинетическая энергия частиц этого тела, а из-за увеличения объема тела увеличится расстояние между молекулами и потенциальная энергия тела. Это приведет к увеличению внутренней энергии тела на величину dU. При увеличении объема рабочего тела оно производит механическую работу dL против сил внешнего давления.

Тогда 1^й закон термодинамики запишется в следующем виде:

δQ = dU + δL = dU + pdV, Дж (1)

Теплота, сообщенная системе, идет на приращение ее внутренней энергии и на совершение внешней работы, (работы изменения объема, работа расширения).

Всегда положительным считается теплота, подведенная к системе и работа, совершенная системой над окружающей средой (внешняя работа). Отрицательным считается теплота, отведенная от системы и работа, совершенная над системой.

Для системы, содержащей 1 кг рабочего тела

δq = du + δl = du + pdυ, Дж/кг (2)

Если уравнения (1) и (2) проинтегрировать, то получим

Введем понятие энтальпии.

Энтальпия - это сумма внутренней энергии системы и произведения давления системы на ее объем:

I = U + pV, Дж

Удельная энтальпия

i = I/M = u + pυ, Дж/кг

Энтальпия очень широко используется в термодинамике. Так как входящие в формулу для энтальпии величины – функции состояния, то энтальпия тоже функция состояния.

Запишем уравнение первого закона термодинамики через энтальпию

δq = du + pdυ = du +d(pυ) – υdp = d(u+pυ) – υdp = di – υdp

В интегральной форме

+ l_расп,

где l_расп - располагаемая (техническая) работа системы.

Приведенные выше формулы справедливы для равновесных, обратимых процессов. Для этих процессов р_внут=р_внеш. Для реальных (неравновесных, необратимых) процессов протекающих с конечной скоростью, за счет вязкости газа и жесткости оболочки будет р_внут>р_внеш, dV_необ<dV и δL_необ < δL:

δL_необ = δL – δL_тр = pdV – δL_тр

Где величина δL_тр характеризует энергию диссипации, которая неизбежно сопровождает реальные процессы.

Тогда первый закон термодинамики для необратимых, реальных процессов можно записать в виде

δQ = dU + δL_необ = dU + δL – δL_тр = dU + pdV – δL_тр

или

δQ + δL_тр = δQ + δQ_тр = dU + δL = dU + pdV

Тема 7.

ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ ДЛЯ ОТКРЫТОЙ ОДНОПОТОЧНОЙ СИСТЕМЫ

Если рассматривать, например, компрессор или турбину, как термодинамическую систему, то она является открытой с одним транзитным стационарным потоком (т.е. эта система обменивается с окружающей средой как веществом, так и энергией). В этих системах рабочее тело движется, то есть совершается рабочий процесс.

По подводящему трубопроводу 1 рабочее тело с параметрами ₁, Т₁, р₁ со скоростью с₁ подается в турбину 2. В турбине каждый кг рабочего тела получает от внешнего источника (из окружающей среды) теплоту q_внеш и совершает техническую работу l_тех, приводя в движение ротор турбины. Затем рабочее тело удаляется из системы через отводящий патрубок 3 со скоростью с₂, имея параметры р₂, Т₂, ₂.

Если в потоке мысленно выделить замкнутый объем рабочего тела и наблюдать за изменениями его параметров в процессе перемещения от входного сечения - к выходному -, то для описания изменения этих параметров можно использовать 1-й закон термодинамики для закрытой термодинамической системы

.

Работа изменения выделенного объема состоит в этом случае из нескольких слагаемых:

1) часть работы затрачивается на преодоление давления р₁ при входе в агрегат, т.е. рассматриваемый объем рабочего тела нужно как бы втолкнуть в агрегат (работа вталкивания), т.к. эта работа производится над рабочим телом, то она отрицательна

;

2) часть работы совершается на подвижных элементах проточной части турбины (т.е. на лопатках) и эта работа является полезной и называется технической работой l_тех;

3) часть работы производится рабочим телом над окружающей средой при выходе (выталкивании) его из отводящего патрубка 3 (работа выталкивания)

;

4) если с₂ ≠ с₁, то часть работы l затрачивается на изменение кинетической энергии рабочего тела в потоке

;

5) если Н₂ ≠ Н₁, то часть работы l затрачивается на изменение потенциальной энергии положения рабочего тела в потоке

g(Н₂ - Н₁);

6) в реальном рабочем процессе часть работы затрачивается на преодоление сил трения l_тр.

В итоге получаем работу изменения объема в виде

,

где работа называется работой вытеснения (или проталкивания).

Теплота q, сообщенная каждому кг выделенного замкнутого объема рабочего тела при прохождении через агрегат, складывается из теплоты, подведенной снаружи q_внеш, и теплоты, в которую переходит работа сил трения внутри агрегата q_тр, т.е.

.

Тогда 1-й закон термодинамики для рассматриваемой системы запишется в виде

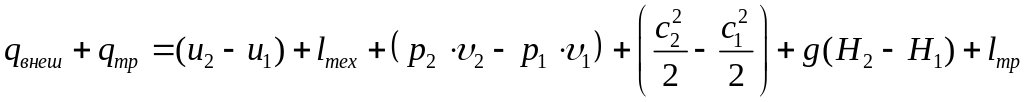
или

. (1)

Теплота, подводимая к потоку извне, расходуется на увеличение энтальпии рабочего тела, производство технической работы и изменение кинетической энергии и потенциальной энергии положения потока.

В дифференциальном выражении имеем

.

Уравнение (1) называют уравнением сохранения энергии в тепловой форме (есть энтальпия). Оно получено при рассмотрении изменения параметров в некотором замкнутом объеме газа, который перемещается от сечения 1-1 до сечения 2-2 через проточную часть турбины. С другой стороны, для этого объема уравнение первого закона термодинамики можно записать в виде

откуда

, т.к. . (2)

Уравнение (2) называют уравнением сохранения энергии в механической форме (есть ).

Из уравнений (1) и (2) получают объединенное уравнение сохранения энергии (уравнение Бернулли)

. (3)

Техническая работа производится за счет располагаемой работы (потенциальной энергии давления) и изменения кинетической энергии и потенциальной энергии положения потока за вычетом потерь на трение. С помощью уравнения (3) удобно анализировать процессы преобразования энергии, происходящие в турбинах.

Для компрессорных машин, в которых техническая работа подводится извне уравнение (3) записываете в виде уравнения сохранения механической энергии

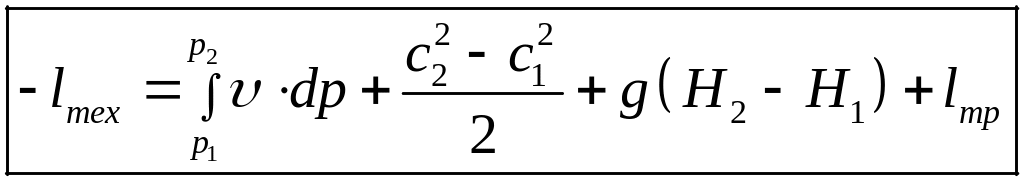(4)

Техническая энергия затрачивается на увеличение потенциальной энергии давления, на изменение кинетической энергии и потенциальной энергии положения потока и покрытие потерь на трение.