Раздел 1 термо-и газодинамические основы сжатия и расширения газов

ТЕМА 1

ИДЕАЛЬНЫЕ И РЕАЛЬНЫЕ ГАЗЫ. УРАВНЕНИЕ СОСТОЯНИЯ ГАЗА

С точки зрения молекулярно-кинетической теории газ представляет собой систему взаимодействующих друг с другом молекул.

Реальный газ – это газ, между молекулами которого действуют силы межмолекулярного взаимодействия (взаимного притяжения, если молекулы находятся на расстоянии, и взаимного отталкивания при достаточном сближении молекул), а сами молекулы имеют конечный объем.

Идеальный газ – это газ, в котором отсутствуют силы межмолекулярного взаимодействия (кроме сил упругого взаимодействия при столкновении молекул), а молекулы представляются материальными точками, не имеющими объема.

Уравнение состояния газа – это уравнение, отражающее функциональную связь между основными термодинамическими параметрами состояния системы (его называют также термическое уравнение состояния). В общем виде

f(p,υ,T)=0 или

p=f₁(υ,T), v=f₂(p,T), T=f₃(p,υ).

Уравнение состояния идеального газа.

Идеальный газ имеет следующие уравнения состояния.

Для М кг газа

. (1)

Для 1 кг газа (уравнение Клапейрона)

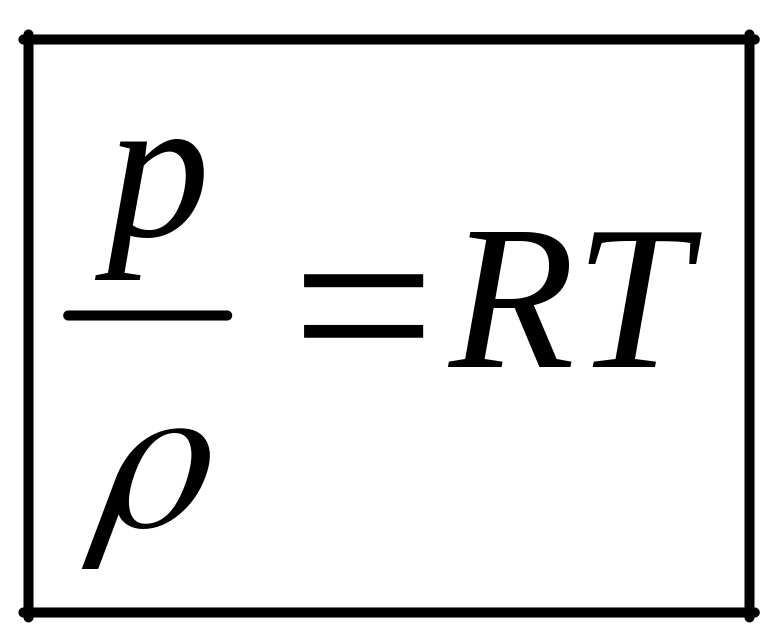или (2)

Для 1 киломоля газа (уравнение Клапейрона-Менделеева)

(3)

В этих уравнениях:

р – абсолютное давление, Па;

Т – абсолютная температура газа, К;

V - объем газа, м³;

M – масса газа, кг;

υ – удельный объем газа, м³/кг;

 - плотность газа, кг/ м³;

- молярный (мольный) объем, м³/кмоль;

- молекулярная масса газа, кг/кмоль;

R – удельная газовая постоянная (газовая постоянная для 1 кг газа), Дж/(кг∙К).;

R_унив – универсальная газовая постоянная (термин, впервые введённый в употребление Д. Менделеевым в 1874 г. Численно равна работе расширения одного моля идеального газа в изобарном процессе при увеличении температуры на 1 К): R_унив=8314, Дж/(кмоль∙К) (более точно - R_унив=8,31441±0,00026, Дж/(моль∙К) или R_унив=8314,41±0,26, Дж/(кмоль∙К)).

Из уравнения (3) видно, что удельная и универсальная газовые постоянные связаны соотношением

,

Продифференцировав уравнение (2) получим уравнение состояния идеального газа в дифференциальной форме

.

Уравнение состояния реальных газов.

Есть много уравнений (более 100), описывающих реальные газы. С точки зрения молекулярно-кинетической теории наиболее подходящим является уравнение Ван-дер-Ваальса

,

где - поправка на давление (молекулярное или внутреннее давление);

b – поправка на объем (наименьший объем до которого можно сжать газ);

a, b – коэффициенты, индивидуальные для каждого газа.

Для многих газов только при очень высоких давлениях влияет объем молекул, и при очень низких давлениях и температурах проявляются силы взаимного притяжения, то есть обычно а/υ²р и bυ. Например, для воздуха использование уравнения состояния идеального газа вместо уравнения состояния реального газа при р10 МПа и Т273 К дает погрешность не более 5 %, т. е. можно принять а/V²≈0 и b≈0.

Очень часто реальность свойств газа учитывается коэффициентом сжимаемости

.

Тогда уравнение состояния реального газа записывается в виде

,

, ,.

Для воздуха при р  10 МПа, Т  273 К можно принимать z ≈1 (см. таблицу).

р, МПА Т,К (t, 0С)	2.5	5
270 (-3)	0.986	0.969
300 (+27)	0.994	0.992
350 (+77)	1.002	1.02

Есть специальные уравнения для определения коэффициента сжимаемости, которые называются также уравнениями состояния в вириальной форме и записываются либо относительно удельного объема, либо относительно давления.

ТЕМА 2

ПЕРВЫЙ И ВТОРОЙ ЗАКОНЫ ТЕРМОДИНАМИКИ