36. Начально-краевая задача для одномерного уравнения теплопроводности. Явная разностная схема: порядок аппроксимации, условие устойчивости. Постановка начально-краевой задачи.
В
области
требуется найти решение уравнения
удовлетворяющее начальному условию
и граничным условиям
Здесь
,
,
— заданные функции.
§ 2. Дискретизация задачи.
Введем сетку по переменному х
и сетку по переменному t с шагом т, которую обозначим
Точки
,
,
,
образуют узлы пространственно-временной
сетки
.
Для
функции
,
определенной на сетке
,
введем обозначения
Шаблоны разностных схем: а) явная схема; б — чисто неявная схема; в — симметричная схема:
Выбираем шаблон а и заменяем в (10.1) производные разностными выражениями, получим явную разностную схему:
Или
Погрешность
аппроксимации явной разностной схемы
:
(сумма погрешностей вычисления
производных).
Утверждение
10.1.
Явную разностную схему можно применять
лишь при условии устойчивости
.
Доказательство. Рассмотрим уравнение
Будем искать частные решения этого уравнения, имеющие вид
где
i
– мнимая единица,
- любое действительное число. Подставляя
в уравнение (10.2) и сокращая на
,
получим
Следовательно,
Если
для некоторого
множитель
станет по модулю больше единицы, то
решение такого вида будет неограниченно
возрастать при
.
В этом случае разностное уравнение
(10.2) называется неустойчивым. Если же
для всех действительных
,
то все решения вида (10.3) ограничены при
любом
и разностное уравнение (10.2) называется
устойчивым.
Неравенство
выполнено тогда и только тогда, когда
или
.
Отметим, что для поиска решения явной разностной схемы требуется решить СЛАУ.
37. Начально-краевая задача для одномерного уравнения теплопроводности. Чисто неявная разностная схема: порядок аппроксимации, устойчивость. Реализация разностной схемы.
Постановка начально-краевой задачи.
В области требуется найти решение уравнения
удовлетворяющее начальному условию
и граничным условиям
Здесь , , — заданные функции.
Чисто неявная разностная схема.
Выбираем шаблон б из последнего рисунка и заменяем в (10.1) производные разностными выражениями, получим чисто неявную разностную схему:
Погрешность
аппроксимации вычисляется аналогично
явной разностной схеме и равна
.
Для нахождения решения нужно решать СЛАУ, как и в случае явной разностной схемы. Но здесь СЛАУ можно решать методом прогонки, так как условия устойчивости прогонки выполнены.
Для исследования устойчивости чисто неявной разностной схемы будем искать частные решения уравнения
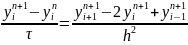
имеющие
вид
.
Тогда получим
следовательно,
при любых
.
Таким образом, схема абсолютно устойчива,
т. е. устойчива при любых шагах
.
Абсолютная устойчивость является
основным преимуществом неявных схем.
Теперь уже не надо брать шаг
слишком малым. Величина шагов сетки
определяется теперь необходимой
точностью расчета, а не соображениями
устойчивости.