35. Разностная схема для краевой задачи для оду 2-го порядка. Аппроксимация, устойчивость и сходимость рс. Исследование рс.

Для сокращения записей далее обозначим

Лемма 9.1. Пусть сеточная функция является решением системы сеточных уравнений

коэффициенты которой удовлетворяют условиям

Тогда если , и для всех то

Коснёмся устойчивости РС.

Пусть - решение разностной схемы , а и — решение разностной схемы

где

Разностная схема устойчива, если при любых справедлива оценка

где постоянная К не зависит от h.

Теорема 9.3. (об устойчивости разностной схемы). Для разностной схемы справедлива оценка (9.10) с постоянной .

Доказательство. Заметим, что сеточная функция 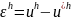является решением разностной схемы

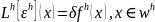
Применяя для оценивания приходим к нужному неравенству.

Определение 9.1. Пусть - решение дифференциального уравнения

Сеточная функция называется погрешностью аппроксимации разностного уравнения

Определение 9.2. Говорят, что разностное уравнение (9.12) аппроксимирует дифференциальное уравнение (9.11), если при , и аппроксимирует его с m-м порядком, если справедлива оценка .

Теорема 9.4. Пусть коэффициенты q и f дважды непрерывно дифференцируемы на отрезке Тогда разностное уравнение аппроксимирует дифференциальное уравнение со вторым порядком, причем справедлива оценка

Доказательство. Прежде всего заметим, что в силу наших знаний по дифференциальным уравнениям функция имеет на отрезке непрерывную производную .

В силу определения погрешности аппроксимации имеем

где - погрешность аппроксимации производной разностной формулой (2-я разностная производная). Таким образом,

Определение 9.3. Пусть — решение краевой задачи, а — решение соответствующей разностной схемы. Назовем погрешностью разностной схемы сеточную функцию , принимающую значения в узлах сетки.

Определение 9.4. Разностная схема сходится при , если при , и сходится с m-м порядком точности (при ), если , где C некоторая постоянная, не зависящая от h.

Теорема 9.5. Пусть функции q и f дважды непрерывно дифференцируемы на отрезке Тогда справедлива оценка

где

Доказательство. Введем сеточную функцию , значения которой в узлах сетки совпадают с точными значениями решения краевой задачи, т. е.

. Функцию можно рассматривать как решение разностной схемы (9.8),(9.9), где , , . В силу теоремы 9.3 для справедлива оценка

Далее с помощью теоремы 9.4 получаем оценку из условия теоремы 9.5.

Замечание 9.1. Мы показали, что разностная схема (9.6), (9.7) сходится со вторым порядком точности.

Замечание 9.2. Пусть и — решения разностной схемы (9.6), (9.7), соответствующие шагам и . Тогда в соответствии с правилом Рунге при определенных условиях справедлива приближенная формула

Отметим, что она применима только в узлах сетки , т. е. там, где определены обе сеточные функции и .