32. Правило Рунге оценки погрешности решения задачи Коши. Идея организации программ с автоматическим выбором шага.

В современных программах, реализующих метод Рунге-Кутты, обязательно используется некоторый алгоритм автоматического изменения шага .

Обычно, на участках плавного изменения функции вычисления можно вести с достаточно крупным шагом, а там где функция резко меняется – с достаточно мелким шагом.

Правило Рунге (без обоснования).

где – точное значение искомой функции в точке , – приближение к , найденное с помощью одношагового метода, порядка точности p,

– приближение к , найденное с помощью двукратного применения одношагового метода:

С помощью правила Рунге можно увеличивать шаг, когда это не даёт больших погрешностей, и уменьшать шаг, когда нужно. Правило Рунге приводит к увеличению времени счёта примерно на 50%. Отметим, что существуют и более экономичные методы оценки локальной погрешности.

33. Краевая задача для ОДУ 2-го порядка. Постановка задачи (в случае постоянного коэффициента теплопроводности). Дискретизация. Построение разностной схемы методом конечных разностей, ее разрешимость.

Рассмотрим уравнение

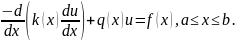
Оно называется стационарным уравнением теплопроводности и возникает при моделировании многих важных процессов. Например, это уравнение описывает установившееся распределение температуры в теплопроводящем стержне длины 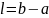. В этом случае 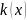– коэффициент теплопроводности, - плотность потока тепла, - коэффициент теплоотдачи, - плотность источников тепла.

Для сокращения записей будем далее обозначать

Для простоты рассмотрим случай постоянного коэффициента теплопроводности .

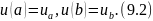
Физическая интерпретация условий (9.2): на торцах стержня поддерживаются фиксированные значения температуры .

§ 2. Дискретизация задачи. Построение разностной схемы (рс) методом конечных разностей.

Заменяем отрезок сеткой - конечным набором точек . Точки называются узлами сетки. Для простоты изложения будем считать сетку равномерной с шагом .

Сетка разбивается на два подмножества: Множество внутренних узлов состоит из тех узлов , которые лежат внутри интервала Множество граничных узлов состоит из двух узлов и .

Мы будем искать решение краевой задачи только в узлах сетки. То есть будем искать не функцию , а сеточную функцию . Значения 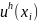будем обозначать через и рассматривать как приближения к значениям решения задачи (9.1), (9.2).

Введём также сеточные функции и , принимающие в узлах сетки значения и .

В (9.1) аппроксимируя 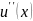второй разностной производной и заменяя значения функций сеточными аналогами, приходим к задаче

)

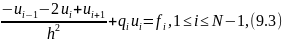
34. Разностная схема для краевой задачи для оду 2-го порядка. Принцип максимума. Априорная оценка решения. Исследование рс.

Для сокращения записей далее обозначим

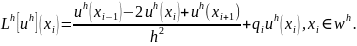
Лемма 9.1. Пусть сеточная функция является решением системы сеточных уравнений

коэффициенты которой удовлетворяют условиям

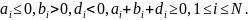
Тогда если , и для всех то

Доказательство. Предположим, что не выполнено. Так как по условию , , то максимальное значение функции положительно и достигается во внутреннем узле сетки: .

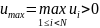Пусть j — максимальный среди индексов i, для которых . Тогда ,

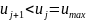
Так как , то . Учитывая, что , , из равенства (9.5), взятого при , получим

Полученное противоречие (0 < 0) доказывает, что .

Теорема 9.1. (принцип максимума). Пусть сеточная функция является решением разностной схемы

Тогда если , и то

Доказательство. Легко проверяется, что коэффициенты системы сеточных уравнений (9.6), (9.7) удовлетворяют условиям леммы 9.1.

Теорема 9.2. Для решения разностной схемы справедлива априорная оценка