28. Явный метод Эйлера решения задачи Коши. Погрешность аппроксимации.

Отбрасывая остаточный член формулы Тейлора, получим приближённое равенство

При , имеем

В силу равенства (8.1), имеем

Или

Метод Эйлера:

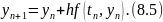
Геометрическая интерпретация одного шага метода Эйлера состоит в аппроксимации решения на касательной .

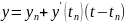Таким образом, после N шагов получаем ломанную Эйлера:

Чтобы определить погрешность аппроксимации метода Эйлера запишем формулу Тейлора с остаточным членом:

или, в силу равенства (8.1):

Поэтому погрешностью аппроксимации для метода Эйлера:

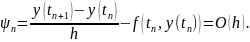
То есть метод Эйлера имеет первый порядок аппроксимации.

Лемма 8.1. Пусть 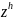- неотрицательная сеточная функция, удовлетворяющая для всех 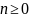неравенству , где . Тогда при всех верна оценка

Теорема 8.2. Пусть f удовлетворяет условию . Тогда справедливо:

означающее, что метод Эйлера устойчив на конечном отрезке.

29. Неявный метод Эйлера решения задачи Коши. Погрешность аппроксимации.

Подставляя вместо правой части выражения (8.9) формулу правых прямоугольников, получаем

и неявный метод Эйлера:

По аналогии с другими методами доказывается, что метод Эйлера имеет первый порядок аппроксимации.

Аналогично теореме 8.2 доказывается

Теорема 8.3. Пусть f удовлетворяет условию . Тогда справедливо неравенство:

означающее, что метод Эйлера устойчив на конечном отрезке.

30. Правило трапеций, метод Эйлера – Коши и усовершенствованный метод Эйлера решения задачи Коши. Получение расчетных формул, порядок аппроксимации.

Интегрируя обе части (8.1) по t от до и используя формулу Ньютона-Лейбница 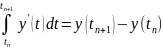получаем

Подставляя вместо правой части выражения (8.9) формулу левых прямоугольников, выводим метод Эйлера.

Подставляя формулу трапеций, получаем:

и правило трапеций:

Порядок аппроксимации этого метода:

Этот метод является неявным, нужно решать нелинейное уравнение относительно .

Подставляя вместо правой части выражения (8.9) формулу центральных прямоугольников

применяя для вычисления метод Эйлера, выводим усовершенствованный метод Эйлера

Это метод также имеет 2-й порядок аппроксимации.

На основе правила трапеций построим явный метод. Для этого подставим в правило трапеций (8.10) значение “предсказываемое” методом Эйлера. В результате получается метод Эйлера-Коши:

Это метод типа предиктор-корректор, на первом этапе вычисляется грубое приближение к по формуле , а затем это значение уточняется.

31. Методы Рунге – Кутты. Общая формула m-этапного метода. Методы Рунге – Кутты 2-го порядка.

Введём на отрезке m вспомогательных узлов , ,…, , где . Заметим, что , . Заменяя входящий в равенство (8.9) интеграл квадратурной суммой с узлами и перенося в правую часть, получаем приближённое равенство

Для нахождения запишем равенства, аналогичные (8.9):

Заменяя для каждого входящий в формулу интеграл соответствующей ему квадратурной формулой с узлами ,…, придём к приближённым равенствам

……………………………………………………………………………………………….

……………………………………………………………………………………………….

Обозначим теперь через вспомогательные величины, имеющие смысл приближений к значениям . Пусть . Тогда расчётные формулы принимают вид

Эти формулы задают явный m-этапный метод Рунге-Кутты.

Теорема 8.4. Пусть правая часть дифференциального уравнения удовлетворяет условию . Тогда всякий явный -этапный метод Рунге-Кутты устойчив на конечном отрезке.

Без доказательства.

Следствие 8.1. (Вытекает из теоремы 8.1.) Пусть . Тогда если явный m-этапный метод Рунге-Кутты имеет p-й порядок аппроксимации, то он сходится с p-м порядком точности.

Выведем расчётные формулы явного двухэтапного метода Рунге-Кутты второго порядка точности. Запишем формулы двухэтапного метода

в виде

Представим погрешность аппроксимации

где , , - решение дифференциального уравнения , в виде разложения по степеням .

Формула Тейлора

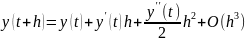
с учётом равенств , даёт формулу

Представим значение функции в точке используя формулу Тейлора для функции двух переменных с центром в точке :

То есть,

Если 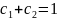, , (что эквивалентно , , ), то два слагаемых в формуле обратятся в 0 и поэтому метод будет иметь второй порядок аппроксимации.

Получили метод второго порядка точности (с учётом следствия 8.1) при любом :

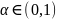Заметим, что при имеем метод Эйлера-Коши, а при 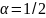- усовершенствованный метод Эйлера.

Пример метода Рунге-Кутты 4-го порядка точности.