26. Численное дифференцирование. Формулы интерполяционного типа. Обусловленность задачи численного дифференцирования.

Требуется найти .

Численное дифференцирование применяется тогда, когда функцию невозможно продифференцировать аналитически. Это происходит, например, когда функция задана таблицей. Кроме того, формулы численного дифференцирования используются при разработке вычислительных методов решения многих задач.

Формулы интерполяционного типа.

Пусть в окрестности точки x функция f аппроксимируется некоторой другой функцией g, причём производная в точке x легко вычисляется. Естественно попытаться использовать формулу .

Пусть – интерполяционный многочлен степени с узлами интерполяции и . Тогда

При этом справедлива оценка погрешности:

Здесь – положительные числа, .

Пример. . Если , то получаем правую разностную производную. Если же – левую.

Обусловленность задачи численного дифференцирования.

Отметим, что при малых шагах формулы численного дифференцирования становятся плохо обусловленными и результат их применения может быть полностью искажён неустранимой ошибкой.

Рассмотрим обусловленность задачи численного дифференцирования на примере вычисления правой разностной производной.

Полная погрешность

Пусть – верхняя граница погрешности используемых значений функции. Тогда, используя (7.4), имеем:

Приравнивая производную , получаем значение оптимального шага

Отметим, что формулы для вычисления производных порядка выше 1 обладают ещё большей чувствительностью к ошибкам задания функций. Поэтому значения производных высокого порядка, найденные с помощью таких формул, могут быть очень неточными.

27. Численное решение задачи Коши для оду 1-го порядка. Постановка задачи. Дискретизация задачи Коши. Явные/неявные методы, одно/многошаговые методы. Устойчивость, аппроксимация, сходимость.

Определение 11.1. Задача нахождения при решения дифференциального уравнения (8.1), удовлетворяющего условию (8.2), называется задачей Коши.

Замечание 11.1. В некоторых случаях надо знать решение при всех . Но чаще ограничиваются определением решения на конечном отрезке

Замечание 8.2. (Геометрический смысл задачи Коши.) Геометрически задача интегрирования дифференциальных уравнений состоит в нахождении кривых, которые в каждой своей точке имеют заданное направление касательной. Чтобы выделить одно конкретное решение задают начальное условие (8.2).

2. Дискретизация задачи.

Заменяем отрезок конечным множеством точек , называемым сеткой . Как правило, будем рассматривать сетки, для которых постоянен. В этом случае и

Далее мы будем рассматривать функции, которые определены только в узлах сетки. Для того чтобы отличать такие функции от функций непрерывного аргумента будем помечать их с помощью индекса h. Например, - сеточная функция. Для краткости будем обозначать .

Далее заменяем уравнением вида

В (8.3) входят значения сеточной функции в последовательных точках . Предполагается, что . Левую часть (8.3) можно рассматривать как аппроксимацию , а правую часть – как аппроксимацию .

Значение приближённого решения в очередной точке находится из (8.3). При этом используются k значений Такие методы называются k-шаговыми.

Проблема страта: необходимо задать k начальных значений

Задачу вычисления сеточной функции , удовлетворяющей при всех уравнению (8.3) и принимающей заданные начальные значения (8.4), будем называть дискретной задачей Коши. Уравнение (8.3) задаёт численный метод решения задачи Коши.

При уравнение (8.3) упрощается и принимает вид

Соответствующий метод принято называть одношаговым. Вычисление осуществляется с использованием только одного предыдущего значения . Поэтому одношаговые методы называют самостартующими.

Определение 8.2. Если функция из уравнения (8.3) не зависит от , соответствующий метод называется явным. Методы, в которых функция зависит от , называются неявными.

Замечание 8.3. При реализации неявных методов приходится решать относительно нелинейное уравнение (8.3).

Пример 8.1. Примером явного метода является метод Эйлера:

.

Примером неявного метода является неявный метод Эйлера:

Определение 8.3. Внесём в правую часть (8.3) и в (8.4) произвольные малые возмущения 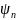и соответственно. Положим . Пусть - решение возмущённой задачи

Дискретная задача Коши (8.3), (8.4) и соответствующий численный метод называются устойчивыми, если при всех (где достаточно мало) справедливо неравенство

где величина не зависит от и .

Уточнение 8.1. Пусть – произвольная гладкая функция. Зафиксируем , устремим h к нулю, n – к бесконечности. Предположим, что коэффициенты из (8.3) удовлетворяют условиям:

Определение 8.4. Пусть y(t) – решение задачи Коши (8.1), (8.2). Погрешностью аппроксимации дискретного уравнения (8.3) на решении y называется сеточная функция , определяемая формулой:

Определение 8.5. Говорят, что дискретное уравнение (8.3) аппроксимирует дифференциальное уравнение (8.1), если при , и аппроксимирует его с p-м порядком, если справедлива оценка .

Определение 8.6. Пусть – решение задачи Коши. Глобальной погрешностью (или просто погрешностью) численного метода называется сеточная функция со значениями в узлах . В качестве меры абсолютной погрешности метода примем величину .

Численный метод решения задачи Коши называется сходящимся, если для него при . Метод сходится с p-м порядком точности, если справедлива оценка , .

Теорема 8.1. Пусть численный метод устойчив на конечном отрезке и имеет порядок аппроксимации равный p. Тогда если начальные значения заданы с p-м порядком точности, то и метод сходится с p-м порядком точности.