Правило Рунге.
Приведём без доказательства следующую формулу (правило Рунге):
где
– порядок точности формулы для вычисления
интеграла.
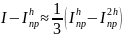
Уточнение
по Рунге
.
Понятие об адаптивных процедурах. Интуитивно ясно, что на участках плавного изменения функции достаточно поместить сравнительно небольшое число узлов, разместив значительно большее их число на участках резкого изменения функции. Часто правильный выбор узлов позволяет при том же числе узлов получать большую точность вычислений. Тем не менее выбор соответствующего неравномерного распределения узлов интегрирования является очень сложной задачей. Но современные программы для ЭВМ более менее умеют это делать.
24. Численное дифференцирование. Левая, правая и центральная разностные производные. Геометрическая интерпретация. Оценки погрешности, порядок точности.
Левая, правая и центральные разностные производные.
Требуется
найти
.
Численное дифференцирование применяется тогда, когда функцию невозможно продифференцировать аналитически. Это происходит, например, когда функция задана таблицей. Кроме того, формулы численного дифференцирования используются при разработке вычислительных методов решения многих задач.
Предположим, что в окрестности точки x функция f дифференцируема достаточное число раз. По определению,
естественно
попытаться использовать для вычисления
формулы:
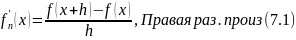
соответствующие
выбору фиксированных значений
и
.
Здесь
– малый параметр (шаг).
Правые части формул (7.1) и (7.2) часто
называют правой
и левой
разностными производными.
Центральная разностная производная:
Для оценки погрешностей воспользуемся формулой Тейлора:
Здесь
и ниже
и
- некоторые точки, расположенные на
и
соответственно. Имеем,
Итак,
Аналогично
устанавливается, что
Для
оценки погрешностей формулы
также
воспользуемся формулой Тейлора:
Получим,
Итак,
Таким образом, формулы (7.1) и (7.2) имеют первый порядок точности по . Иначе говоря, правая и левая разностные производные аппроксимируют с первым порядком точности относительно , а центральная разностная производная – со вторым порядком.
25. Численное дифференцирование. Вторая разностная производная. Оценка погрешности, порядок точности.
Требуется найти .
Численное дифференцирование применяется тогда, когда функцию невозможно продифференцировать аналитически. Это происходит, например, когда функция задана таблицей. Кроме того, формулы численного дифференцирования используются при разработке вычислительных методов решения многих задач.
Для вычисления второй производной широко применяется формула
Правую часть (10.4) часто называют второй разностной производной.
Для
оценки погрешностей формулы
воспользуемся
формулой Тейлора:
Получим,
Итак,
Таким образом, формула (7.5) имеет второй порядок точности.